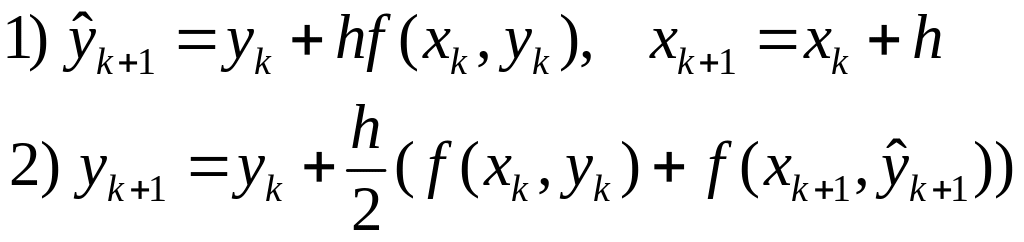Ошибка метода Эйлера

Представленный метод аппроксимации решения задачи Коши называется разностным. Решение представляет собой совокупность отдельных точек, называемых узловыми.

При использовании разностных методов существует два источника ошибок: ошибка дискретизации, возникающая в результаты замены дифференциального уравнения разностной аппроксимацией (2.5), и ошибка округления, накопившаяся при выполнении арифметических операций. Будем считать, что значения вычисляются точно, так что погрешности обусловлены только ошибкой дискретизации. Введем величину, равную наибольшему отклонению аппроксимации от точного решения на отрезке

(3.1)

называемую глобальной ошибкой дискретизации (иногда эту величину называют глобальной ошибкой усечения). Отметим, что зависит от величины шага , поскольку предполагается, что приближения вычисляют при заданном значении . Интуитивно ожидаем, что при уменьшении ошибка дискретизации будет убывать и, в частности, при стремлении к нулю, так же будет стремиться к нулю.

Теорема (ошибка дискретизации метода Эйлера). Если функция имеет ограниченную частную производную по второй переменной и если решение задачи Коши имеет ограниченную вторую производную, то глобальная ошибка дискретизации метода Эйлера .

Порядок метода численного интегрирования показывает, от какой степени шага зависит величина ошибки.

Локальная (или шаговая) ошибка метода – это ошибка, совершаемая на одном шаге. Очевидно, что от шага к шагу, т. е. при многократном применении формулы метода, возможно наложение ошибок. За шагов, т. е. в точке , образуется глобальная ошибка.

Порядок глобальной ошибки (относительно шага ) на единицу ниже, чем порядок локальной ошибки, а порядком глобальной ошибки и определяется порядок соответствующего численного процесса решения задачи Коши.

Глобальная ошибка метода Эйлера есть , т. е. данный метод имеет первый порядок. Иными словами, размер шага и ошибка для метода Эйлера связаны линейно. Практическим следствием этого факта является ожидание того, что при уменьшении приближенное решение будет все более точным и при стремлении к нулю будет стремиться к точному решению с линейной скоростью ; т.е. ожидаем, что при уменьшении шага вдвое ошибка уменьшится примерно в два раза. Такое поведение ошибки демонстрируется на следующем примере.

Поскольку в методе Эйлера ошибка достаточно велика и от шага к шагу накапливается, а точность пропорциональна количеству вычислений, то метод Эйлера обычно применяют для грубых расчетов, для оценки поведения системы в принципе. Для точных количественных расчетов применяют более точные методы.

Метод Хьюна

Следующий подход представляет новую идею построения алгоритмов решения задачи Коши. Пусть

на отрезке с начальным условием

Для получения решения в точке , можем воспользоваться теоремой о вычислнии определенного интеграла:

где первообразная от является искомой функцией . Если разрешить уравнение последнее уравнение относительно , получим

Теперь можно применить численные методы нахождения интеграла. Воспользуемся методом трапеций с шагом , получим:

Правая часть формулы включает в себя еще не найденное значение . Для его нахождения воспользуемся методом Эйлера. Получим конечную формулу, именуемую методом Хьюна (синонимы: метод Хойна, метод Эйлера-Коши):

Продолжая процесс, получим последовательность точек, аппроксимирующих кривую решения . Метод Хьюна относится к классу методов прогноза-коррекции. На каждом шаге метод Эйлера используется для предсказания, а метод трапеций для уточнения конечного значения. Общие формулы для шага метода Хьюна: