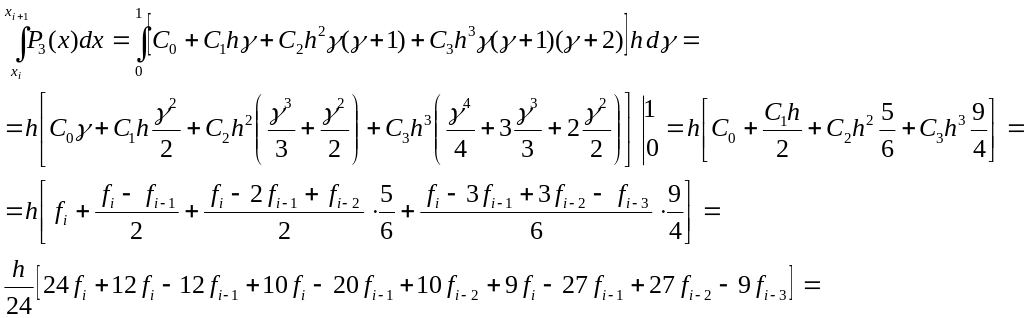- •Основные понятия и определения
- •Метод эйлера
- •Ошибка метода Эйлера
- •Метод Хьюна
- •Методы Рунге-КуттЫ.
- •Явные одношаговые методы численного решения обыкновенных дифференциальных уравнений с автоматическим выбором шага интегрирования
- •Метод рунге-кутта четвертого порядка точности с автоматическим контролем шага
- •Метод рунге-кутта-мерсона с контролем шага
- •Метод фельдберга с контролем шага
- •Метод ингленда с контролем шага
- •Многошаговые методы численного интегрирования дифференциальных уравнений
- •Методы Адамса-Башфорта
- •Методы Адамса-Моултона
- •Методы прогноза-коррекции
Многошаговые методы численного интегрирования дифференциальных уравнений
Одношаговые
методы численного решения ДУ для
нахождения значения
в последующей точке
![]() используют только решение в точке
используют только решение в точке
![]() .
В этом разделе будут изложены многошаговые
методы, использующие для решения задачи
Коши информацию о нескольких точках.
Широко распространенным семейством
многошаговых методов являются методы
Адамса.
Различают явные
и неявные
многошаговые методы. Явные многошаговые
методы используют явную схему (по
известным значениям функции в предыдущих
узлах находится значение в последующем
узле
).
К классу неявных методов относятся
методы, использующие информацию о
последующих и предыдущих точках.
.
В этом разделе будут изложены многошаговые
методы, использующие для решения задачи
Коши информацию о нескольких точках.
Широко распространенным семейством
многошаговых методов являются методы
Адамса.
Различают явные
и неявные
многошаговые методы. Явные многошаговые
методы используют явную схему (по
известным значениям функции в предыдущих
узлах находится значение в последующем
узле
).
К классу неявных методов относятся
методы, использующие информацию о
последующих и предыдущих точках.
К явной группе относятся методы Адамса-Башфорта, к неявной – методы Адамса-Моултона.
Методы Адамса-Башфорта
Пусть
дано уравнение
![]() с начальным условием
с начальным условием
![]() .
.
, |
(28) |
Многошаговые
методы численного интегрирования
основываются на интерполяции правой
части уравнения (28). Запишем это уравнение
в виде
![]() и проинтегрируем его на отрезке
и проинтегрируем его на отрезке
![]() :
:
|
|
где
![]() - точное значение функции
в точке
- точное значение функции
в точке
![]() .
.
Идея
состоит в том, чтобы заменить
![]() функцией, интеграл от которой легко
вычисляется. Существует множество типов
интерполирующих функций; в этом разделе
рассмотрим методы, связанные с
полиномиальной интерполяцией. Функция
заменяется полиномом
функцией, интеграл от которой легко
вычисляется. Существует множество типов
интерполирующих функций; в этом разделе
рассмотрим методы, связанные с
полиномиальной интерполяцией. Функция
заменяется полиномом
![]() степени
,
таким, что
степени
,
таким, что
![]() (многочлен аппроксимирует функцию
на отрезке
по значениям
(многочлен аппроксимирует функцию
на отрезке
по значениям
![]() ).
).
Общая формула явного метода Адамса:
|
|
где
![]() - приближенные значения, найденные с
помощью численного метода.
- приближенные значения, найденные с
помощью численного метода.
Явно интегрируя многочлен, получают формулы численного решения ДУ.
Простейший
метод Адамса получается при
![]() и совпадает с методом Эйлера первого
порядка точности:
и совпадает с методом Эйлера первого
порядка точности:
|
(29) |
При
![]() (порядок метода
(порядок метода
![]() )
многочлен задает прямую, проходящую
через точки
)
многочлен задает прямую, проходящую
через точки
![]() .
.

Рис.1.
Интерполяционный
многочлен Ньютона (далее ИМН) на
![]() :
:
|
|
Подставим
значения
![]() ,
,
![]() :
:
|
|
Проинтегрируем
полином и подставим значения коэффициентов
![]() :
:
|
|
Получили формулу двухшагового метода Адамса-Башфорта:
|
(30) |
Чтобы
начать решение по формуле (3), необходимо
знать значение
![]() .
.
Для запуска решения используется одношаговый метод того же порядка (для данного случая - метод Эйлера с пересчетом (метод трапеций), модифицированный метод Эйлера и т. д.):
|
|
Дальше работает только многошаговый метод:
|
|
Пример
1:
![]() ,
,
![]() ,
,
![]() .
.
Аналитическое
решение:
![]() .
.
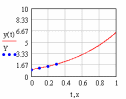
Рис.2.
Сведем это уравнение к СДУ второго порядка:
|
|
Запишем систему в векторной форме:
|
|
Используем явный двухшаговый метод (30):
|
|
Возьмем
![]() .
.
Первые две точки решения получим одношаговым методом трапеций:
|
|
Теперь у нас достаточно данных для продолжения решения только двухшаговым методом:
|
|
Пусть
![]() ,
есть квадратичный полином, интерполирующий
данные
,
есть квадратичный полином, интерполирующий
данные
![]() (рис. 3).
(рис. 3).
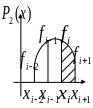
Рис.3.
Итерполяционный
многочлен Ньютона, построенный по этим
точкам,
![]()
Найдем коэффициенты интерполяционного многочлена:
|
|
Определим значение интеграла
|
|
Введем замену переменных
|
(31) |
Тогда:

Определенный интеграл:
|
|
Формула трехшагового метода Адамса-Башфорта имеет вид:
|
(32) |
Решение запускается с помощью одношагового метода третьего порядка точности:
|
|
В
практических расчетах чаще всего
используется вариант метода Адамса,
имеющий четвертый порядок точности и
использующий на каждом шаге результаты
предыдущих четырех (![]() ,
интерполяционный многочлен здесь
является кубическим полиномом). Именно
его и называют обычно методом
Адамса:
,
интерполяционный многочлен здесь
является кубическим полиномом). Именно
его и называют обычно методом
Адамса:
|
(33) |
Методы более высоких порядков получаются при увеличении числа предыдущих точек. С ростом степени многочлена формулы становятся более громоздкими, но принцип остается тем же.
Для запуска решения используется метод Рунге-Кутта того же порядка.
Получим формулу (33).
Итерполяционный многочлен Ньютона:
|
|
Пусть
![]() .
.
Определим
разность первого порядка функции
![]() как
как
![]() ,
а разности более высокого порядка как
результат повторного применения этой
операции:
,
а разности более высокого порядка как
результат повторного применения этой
операции:
|
(34) |
С помощью разностей (7) определим полином степени N как:
|
(35) |
При
![]() многочлен примет вид:
многочлен примет вид:
|
|
Введя замену (34), получим:
|
|
Найдем интеграл:
|
|
Отсюда непосредственно следует формула (33).
Объем
вычислений по методу Адамса примерно
в четыре раза меньше, чем в методе
Рунге-Кутта, поскольку последний требует
четырехкратного вычисления правой
части уравнения на каждой итерации, а
в методе Адамса правая часть вычисляется
один раз; остальные значения (![]() ,
,
![]() и
и
![]() )
однократно вычисляются на предыдущих
трех итерациях и пересылаются в текущую
итерацию простым копированием. Такая
экономия особенно существенна, если в
правой части ДУ стоит сложное аналитическое
выражение.
)
однократно вычисляются на предыдущих
трех итерациях и пересылаются в текущую
итерацию простым копированием. Такая
экономия особенно существенна, если в
правой части ДУ стоит сложное аналитическое
выражение.

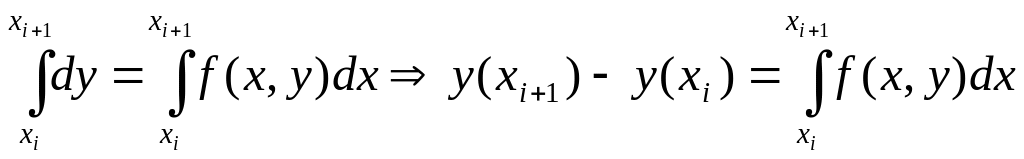
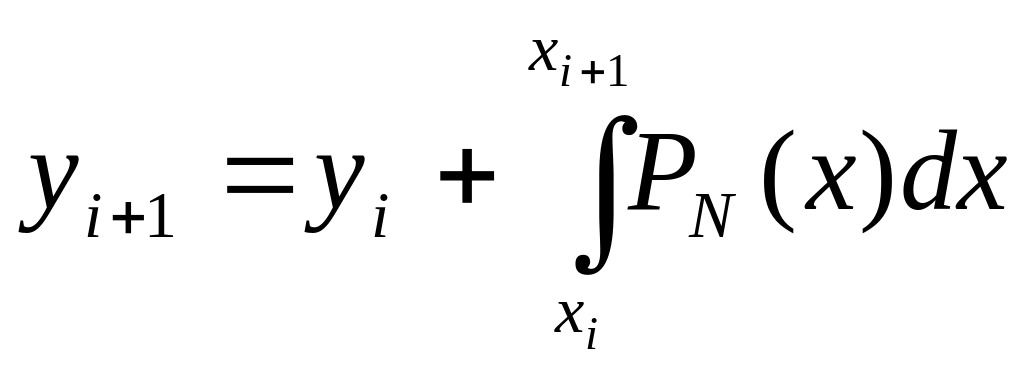
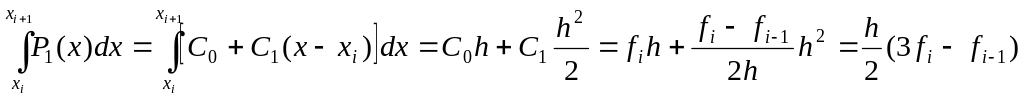
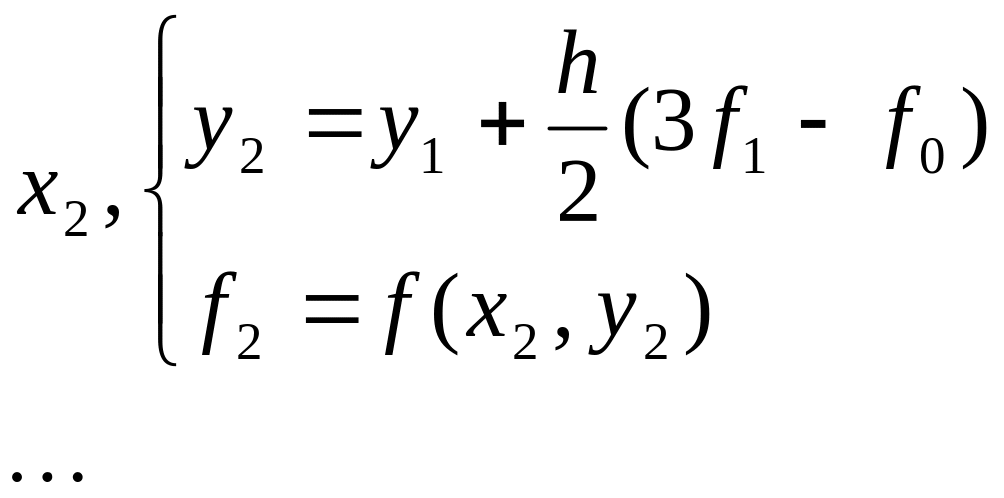
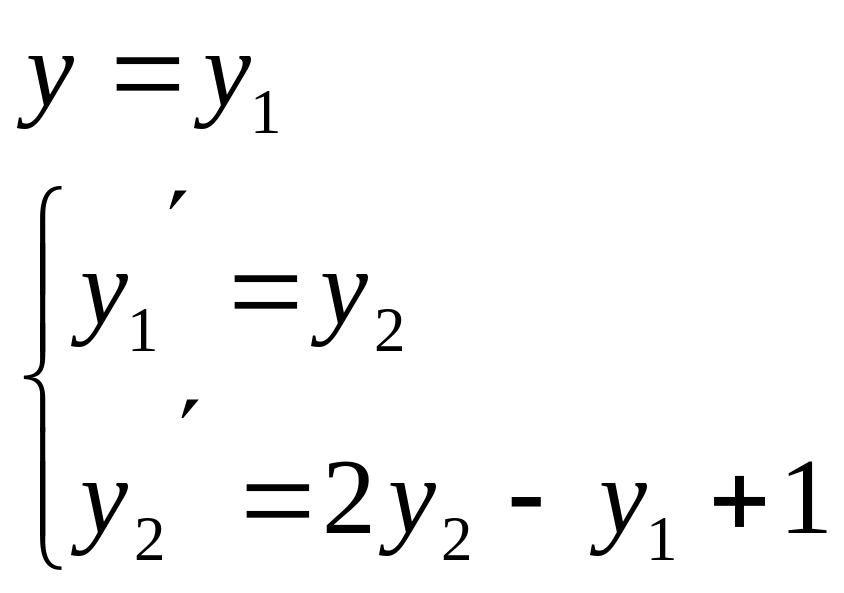
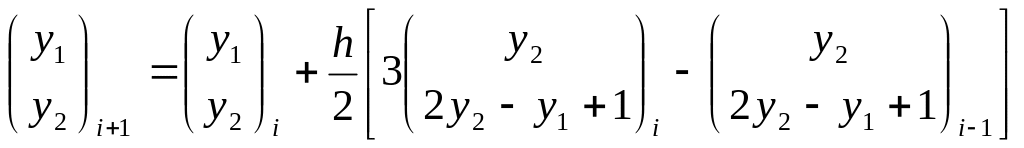 .
.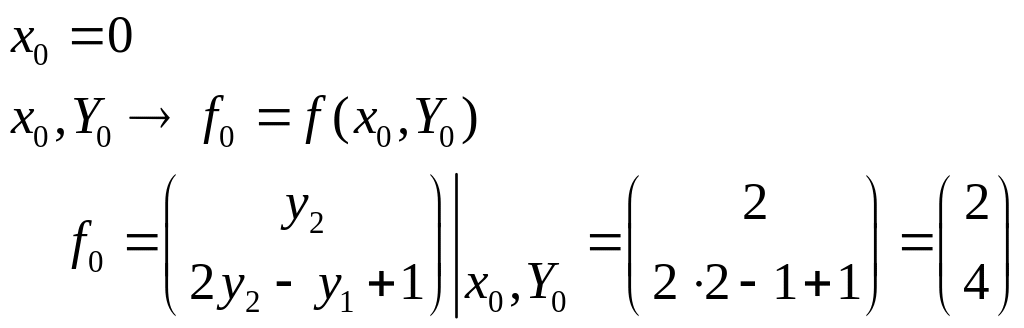

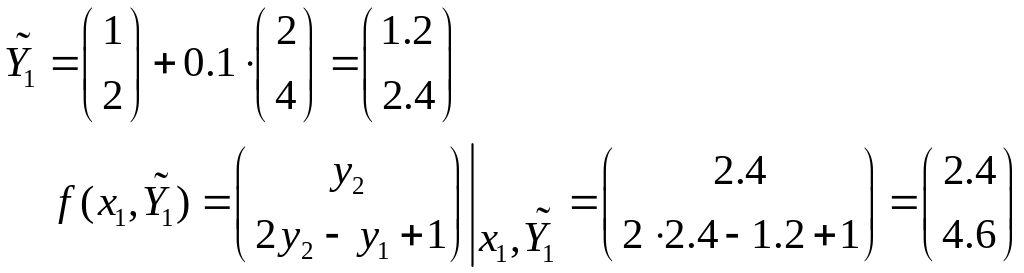

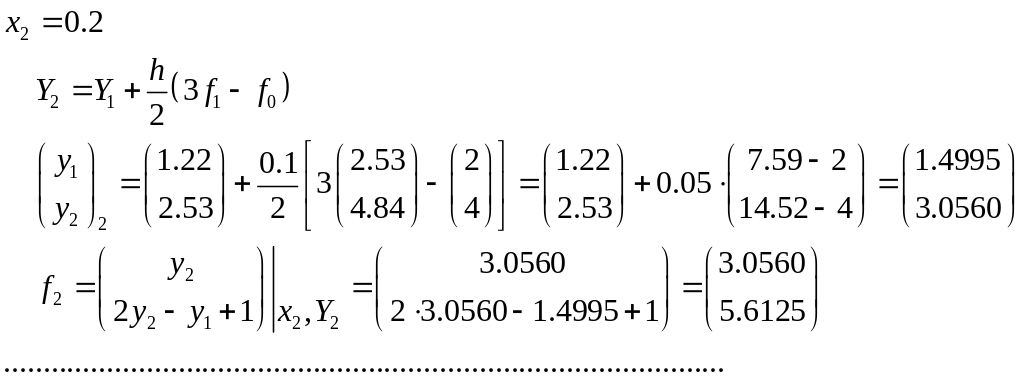
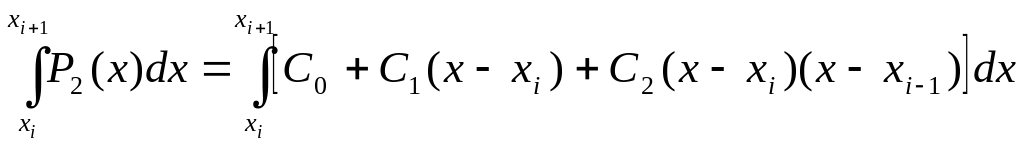 .
.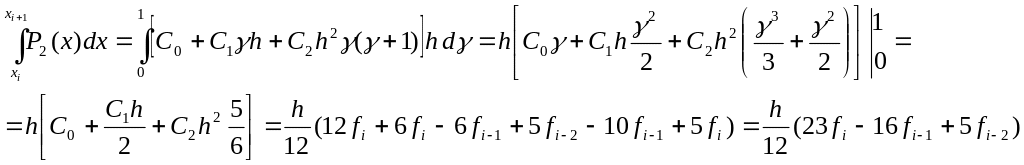
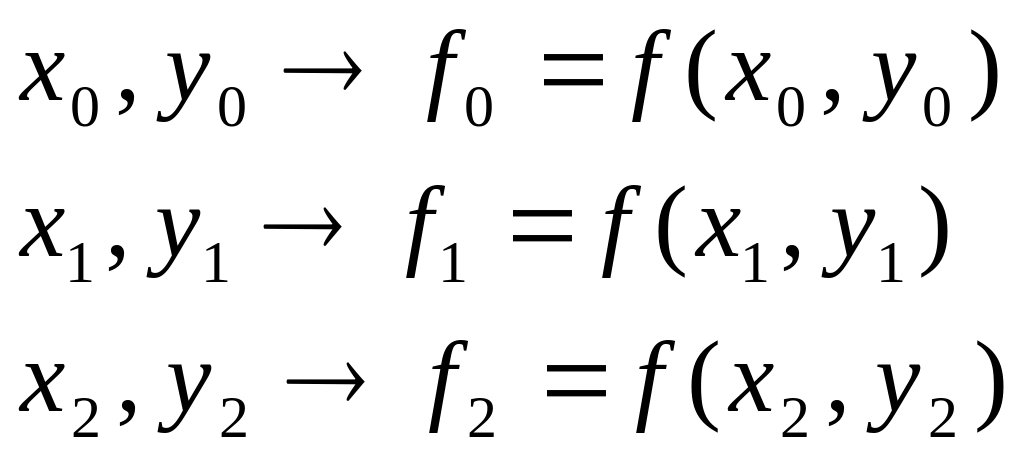 ,
,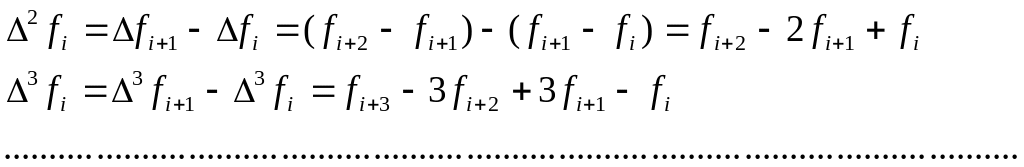
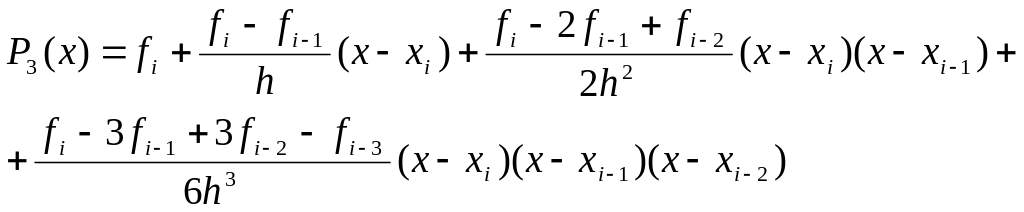 ,
,