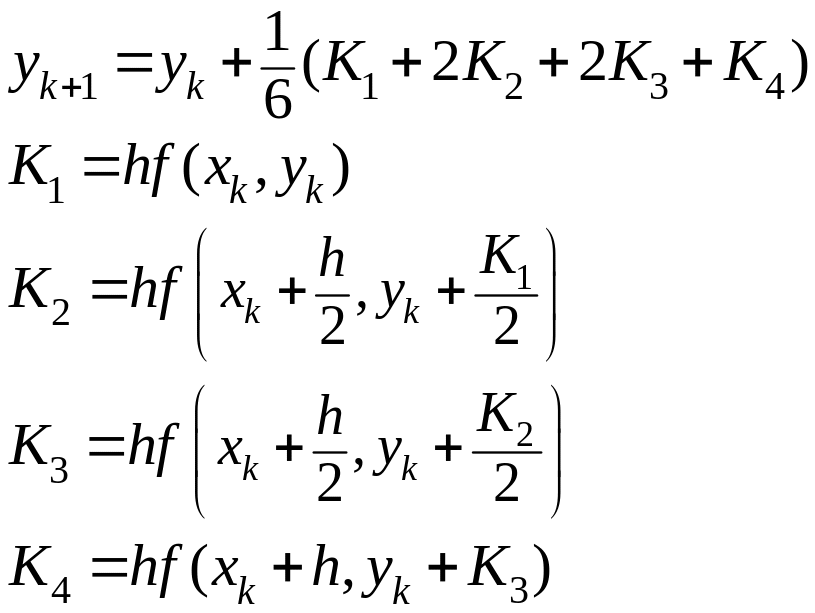Методы Рунге-КуттЫ.

Методы Тейлора обладают глобальной ошибкой , и может быть выбрано настолько большим, насколько малой необходимо получить эту ошибку. Тем не менее, у методов Тейлора есть очевидные недостатки. Это необходимость задавать заранее и необходимость вычисления производных высших порядков, что может быть очень сложной задачей. Любой метод Рунге-Кутты получается из метода Тейлора соответствующего порядка. Необходимость вычисления производных высших порядков заменяется многократным пересчетом функции. Эти методы могут быть получены для любого порядка . Метод Рунге-Кутты 4-го порядка является наиболее популярным. Это хороший выбор для многих целей, т. к. обладает высокой точностью, стабильностью и легкостью в программировании. Методы Рунге-Кутты более высоких порядков применяются редко, так как рост вычислительных затрат перекрывает полученный прирост точности. Если необходима большая точность, следует уменьшить шаг, либо использовать более адаптивный метод.

Результирующие формулы:

Явные одношаговые методы численного решения обыкновенных дифференциальных уравнений с автоматическим выбором шага интегрирования

Данная группа методов является модификацией предыдущих методов численного интегрирования с целью сокращения временных затрат на вычислительный процесс. Это достигается коррекцией величины шага интегрирования в зависимости от текущего значения погрешности р, которая оценивается по конкретному выражению для каждого метода.

Исходные данные при этом аналогичны предыдущим методам, к которым добавляется задаваемая точность ε поиска решения дифференциального уравнения.

Алгоритм выбора величины шага интегрирования включает следующие операции, которые реализуются при вычислении каждого значения функции на шаге интегрирования:

Пусть р_i+1 оценка локальной погрешности метода на шаге h , допущенной при вычислении приближенного значения решения в точке x_i+h. Если оценка превосходит некоторую наперед заданную границу ε :

|p_i+1|> ε,

то считается, что значение решения не удовлетворяет предписанной точности, и шаг h объ­является неприемлемым. Полученная точка x_i+h и значение у^h_i+1 исключаются из рассмотрения. Выбирается новое значение шага

и вновь по той же формуле Рунге-Кутта с шагом h⁽¹⁾ вычисляется новое значение решения у^h(1)_i+1 в новой точке х_i+h⁽¹⁾.

Пусть p⁽¹⁾_i+1 - оценка локальной погрешности метода на данном шаге h⁽¹⁾. Если оценка опять превосходит заданную границу ε :

|p⁽¹⁾_i+1|> ε,

то точка х_i+ h⁽¹⁾ и значение y^h(1)_i+1 опять исключаются из рассмотрения, шаг снова делится пополам:

и вычисления повторяются. Так происходит до тех пор, пока при какой-то величине шага (обо­значим ее через h⁽ⁿ⁾) оценка локальной погрешности не станет меньше ε :

|p⁽ⁿ⁾_i+1| ε.

После этого считается, что решение дифференциального уравнения продолжено до точки x_i+1 = х_i + h⁽ⁿ⁾. Дальнейшее интегрирование уравнения производится из точки х_i+1 с шагом h⁽ⁿ⁺¹⁾, который выбирается описанным ниже способом.

Если оценка локальной погрешности на шаге h⁽ⁿ⁾ = х_i+1 – х_i удовлетворяет неравенству

где К - некоторая константа, то считается, что достигнута точность, превышающая заданную, и шаг интегрирования удваивается:

h⁽ⁿ⁺¹⁾ = 2h⁽ⁿ⁾.

Если выполняется неравенство

,

то считается, что полученное в точке х_i+1 решение удовлетворяет заданной точности и шаг интегрирования остается без изменения

h⁽ⁿ⁺¹⁾ = h⁽ⁿ⁾.

Таким образом, на тех участках изменения независимой переменной, где достигается вы­сокая точность приближенного решения, шаг интегрирования возрастает, а там, где точность не достигается, шаг интегрирования сокращается до необходимых для ее достижения значе­ний. Тем самым обеспечивается выбор величины шага в зависимости от характера поведения решения дифференциального уравнения. Константа К обычно полагается равной 2^s+1 , где s – порядок точности метода.¹

Остановимся более подробно на конкретных методах с автоматическим шагом интегрирования.