Требования к содержанию и оформлению отчёта

Отчёт выполняется машинописным способом на листах формата А4, текст располагается с одной стороны. Титульный лист стандартной формы, с указанием темы работы, номера варианта, ФИО и номера группы студента, ФИО и должности преподавателя. Листы отчёта помещаются в скоросшиватель. Допускается скреплять листы степлером и помещать в полиэтиленовый файл.

Отчёт должен включать в себя следующие разделы:

1. номер варианта и соответствующее ему условие задачи;

2. уравнения прямых, задающих область допустимых значений параметров;

3. график, на котором отмечена область значений параметров;

4. таблица значений целевой функции в точках, являющихся вершинами области допустимых значений параметров;

5. искомые значения параметров.

Контрольные вопросы

1. Возможно ли применение геометрического способа для решения задач, в которых целевая функция имеет более двух параметров?

2. В чём состоит суть графического метода?

3. Какова геометрическая интерпретация ограничений, задаваемых на значения параметров целевой функции?

Лабораторная работа №3

Решение задачи о кратчайшем пути Цель работы

Изучение методики выбора оптимального маршрута доставки в задачах, условия которых формализованы в виде ориентированного графа.

Краткие теоретические сведения

В повседневной практике часто возникают задачи, связанные с перемещением материальных объектов из одного пункта в другой, причём для этого существует множество возможных маршрутов, состоящих из последовательности отдельных пунктов. Задача состоит в нахождении оптимального маршрута, перемещение по которому потребует наименьших затрат.

Условия этой задачи можно формализовать в виде взвешенного ориентированного графа (орграфа)⁵. Например, для выбора оптимального маршрута перевозки грузов по городу можно принять, что вершинами орграфа являются перекрёстки улиц, рёбрами – отрезки улиц между перекрёстками, весами – расстояние между вершинами.

Каждые две вершины могут соединять соединяют две дуги - туда и обратно, имеющие разный вес. Действительно, если пункт А расположен на горе, а пункт Б - в низине, то время на проезд из А в Б, очевидно, меньше времени на обратный проезд из Б в А. Каждая вершина может быть посещена не более одного раза.

Взвешенный орграф может быть задан как графически, так и с помощью матрицы размерностью , где – количество вершин графа. Число , находящееся в ячейке матрицы , является весом ребра, соединяющего -ю и -ю вершины. Если ячейка пуста, то это означает, что из -й вершины в -ю перемещение невозможно.

Оптимизационные задачи на графах, возникающие при подготовке управленческих решений, весьма многообразны.

Методические указания

Рассмотрим методику поиска кратчайшего пути на примере. Пусть имеется орграф, представленный на рисунке 1.

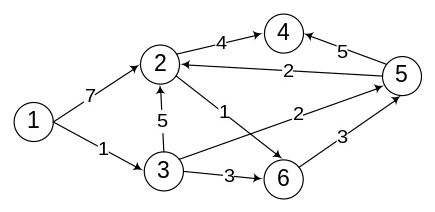
Рисунок 1 – Исходные данные к задаче в виде взвешенного орграфа.

Приведённый граф может быть записан также в виде таблицы 4.1.

Исходные данные к задаче в табличной форме. Таблица 4.1.

j i		Номера вершин
		1	2	3	4	5	6
Номера вершин	1		7	1
	2				4		1
	3		5			2	3
	4
	5		2		5
	6					3

Пусть необходимо найти кратчайший путь между вершинами 1 и 4.

Введем обозначение: С(Т) - длина кратчайшего пути⁶ из вершины 1 в вершину Т.

Поставленная задача состоит в вычислении С(4) и указании пути с минимальной стоимостью проезда.

Рассмотрим подробнее взвешенный орграф, представленный на рисунке 1.

В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение

С(4) = min {С(2) + 4; С(5) + 5}.

Таким образом, проведена реструктуризация (упрощение) задачи - нахождение С(4) сведено к нахождению С(2) и С(5). 

 В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение

С(5) = min {С(3) + 2; С(6) + 3}.

В вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, следовательно

С(3) = 1.

Поэтому

С(5) = min {1+2; С(6) + 3}= min {3; С(6) + 3}.

Поскольку очевидно, что С(6) - положительное число, то из последнего соотношения вытекает, что

С(5) = 3,

т.е. вычислять значение С(6) не имеет смысла, поскольку выражение С(6) + 3 всегда будет больше 3.

 В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение

С(2) = min {С(1) + 7; С(3) + 5; С(5) + 2}.

Очевидно, что С(1) = 0. Нам известно, что С(3) = 1, С(5) = 3. Поэтому

С(2) = min {0 + 7; 1 + 5; 3 + 2} = min {7; 6; 5} = 5.

Теперь мы можем найти С(4):

С(4) = min {С(2) + 4; С(5) + 5} = min {5 + 4; 3 + 5} = min {9; 8} = 8.

Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков:

1 → 3 → 5 → 4 .

Задача о кратчайшем пути для исходных данных полностью решена.