7. Обработка и анализ результатов моделирования систем

Успех имитационного эксперимента с моделью системы существенным образом зависит от правильного решения вопросов обработки и последующего анализа и интерпретации результатов моделирования. Особенно важно решить проблему текущей обработки экспериментальной информации.

7.1. Особенности фиксации и статистической обработки результатов моделирования систем на эвм

Особенности машинных экспериментов. После того как машинный эксперимент спланирован, необходимо предусмотреть меры по организации эффективной обработки и представления его результатов.

При выборе методов обработки существенную роль играют три особенности машинного эксперимента с моделью системы S:

1. большие выборки позволяют количественно оценить характеристики процесса функционирования системы, но появляется серьезная проблема хранения промежуточных результатов моделирования. Эту проблему можно решить, используя рекуррентные алгоритмы обработки, когда оценки вычисляют по ходу моделирования, причем большой объем выборки дает возможность пользоваться при этом достаточно простыми для расчетов на ЭВМ асимптотическими формулами;

2. априорное суждение о характеристиках процесса функционирования системы, например, о типе ожидаемого распределения выходных переменных, является невозможным из-за сложности исследуемой системы. Поэтому при моделировании систем широко используются непараметрические оценки и оценки моментов распределения;

3. блочность конструкции машинной модели М_м и раздельное исследование блоков связаны с программной имитацией входных переменных для одной частичной модели по оценкам выходных переменных, полученных на другой частичной модели.

Методы оценки. Рассмотрим наиболее удобные для программной реализации методы оценки распределений и некоторых их моментов при достаточно большом объеме выборки (числе реализаций N). Математическое ожидание и дисперсия случайной величины  соответственно имеют вид:

;

,

где f(x) – плотность распределения случайной величины , принимающей значения х.

При проведении имитационного эксперимента со стохастической моделью системы S определить эти моменты нельзя, так как плотность распределения, как правило, априори неизвестна. Поэтому при обработке результатов моделирования получают лишь некоторые оценки моментов, полученные на конечном числе реализации N. При независимых наблюдениях значений случайной величины  в качестве таких оценок используются

;

,

где и – выборочное среднее и выборочная дисперсия соответственно. Знак ~ над и означает, что эти выборочные моменты используются в качестве оценок математического ожидания _ и дисперсии .

К качеству оценок, полученных в результате статистической обработки результатов моделирования, предъявляются следующие требования:

1. несмещенность оценки, т.е. равенство математического ожидания оценки определяемому параметру M[ 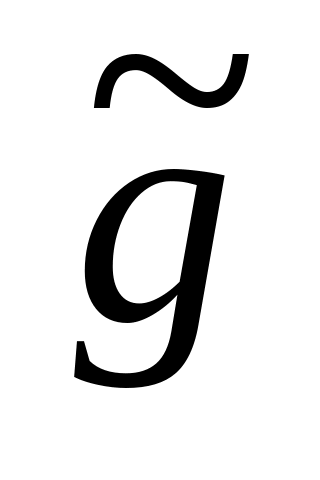] = g, где – оценка переменной (параметра) g;

2. эффективность оценки, т.е. минимальность среднего квадрата ошибки данной оценки M[ 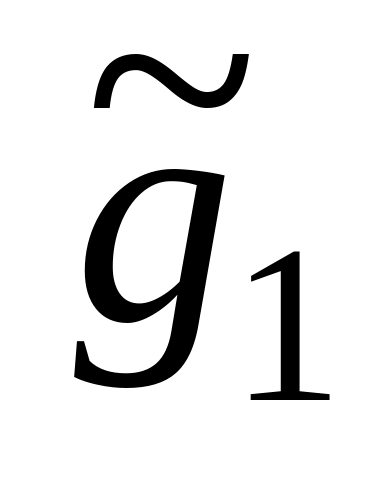 – g]M[( 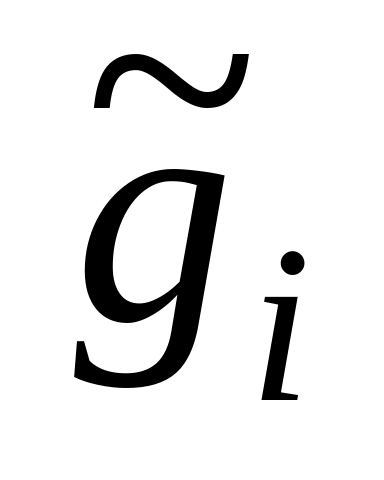 – g)²], где – рассматриваемая оценка; – любая другая оценка;

3. состоятельность оценки, т.е. сходимость по вероятности при N к оцениваемому параметру 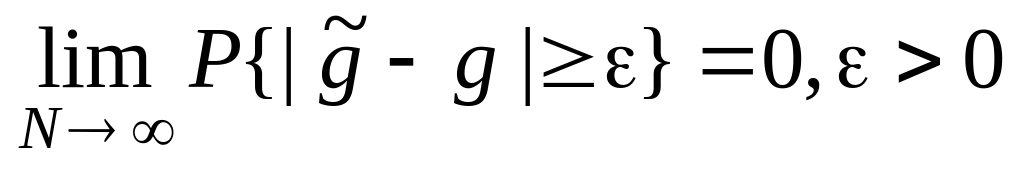, либо, учитывая неравенство Чебышева, достаточное (но не обязательно необходимое) условие выполнения этого неравенства заключается в том, чтобы .

Рассмотрим оценку выборочного среднего значения . Математическое ожидание выборочного среднего значения x составит

,

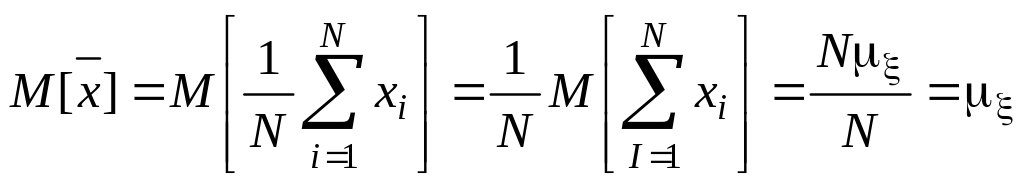т. е. оценка = является несмещенной.

С учетом независимости значений x_i средний квадрат ошибки

,

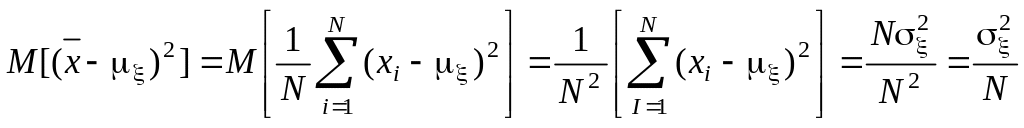т.е. оценка = состоятельна. Можно показать, что эта оценка также и эффективна.

Рассмотрим оценку выборочной дисперсии . Математическое ожидание выборочной дисперсии

.

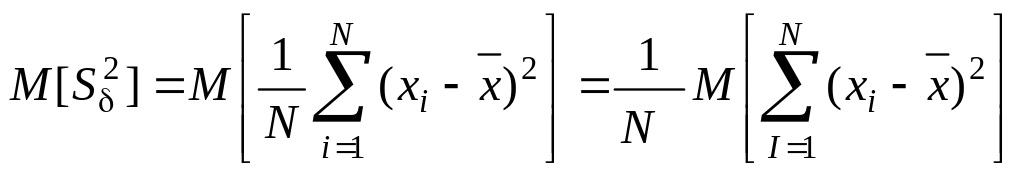Учитывая, что

получим M[ ]=(N – 1) /N, т.е. оценка = является смещенной. Можно показать, что эта оценка состоятельна и эффективна.

Несмещенную оценку дисперсии можно получить, вычисляя выборочно дисперсию вида

.

Эта оценка также удовлетворяет условиям эффективности и состоятельности.

Статистические методы обработки. Рассмотрим некоторые особенности статистических методов, используемых для обработки результатов моделирования системы S. Для случая исследования сложных систем при большом числе реализации N в результате моделирования на ЭВМ получается значительный объем информации о состояниях процесса функционирования системы. Поэтому необходимо так организовать в процессе вычислений фиксацию и обработку результатов моделирования, чтобы оценки для искомых характеристик формировались постепенно по ходу моделирования, т.е. без специального запоминания всей информации о состояниях процесса функционирования системы S.

Если при моделировании процесса функционирования конкретной системы S учитываются случайные факторы, то и среди результатов моделирования присутствуют случайные величины. В качестве оценок для искомых характеристик рассчитывают средние значения, дисперсии, корреляционные моменты и т.д.

Пусть в качестве искомой величины фигурирует вероятность некоторого события А. В качестве оценки для искомой вероятности р=Р(А) используется частость наступления события m/N, где т – число случаев наступления события А; N – число реализаций. Такая оценка вероятности появления события А является состоятельной, несмещенной и эффективной. В случае необходимости получения оценки вероятности в памяти ЭВМ при обработке результатов моделирования достаточно накапливать лишь число т (при условии, что N задано заранее).

Аналогично при обработке результатов моделирования можно подойти к оценке вероятностей возможных значений случайной величины, т.е. закона распределения. Область возможных значений случайной величины  разбивается на п интервалов. Затем накапливается количество попаданий случайной величины в эти интервалы m_k, . Оценкой для вероятности попадания случайной величины в интервал с номером k служит величина m_k/N. Таким образом, при этом достаточно фиксировать n значений m_k при обработке результатов моделирования на ЭВМ.

Для оценки среднего значения случайной величины  накапливается сумма возможных значений случайной величины у_k, , которые она принимает при различных реализациях. Тогда среднее значение

.

При этом ввиду несмещенности и состоятельности оценки

М[ ] = М[] = _; D[ ] = D[]/N = /N.

В качестве оценки дисперсии случайной величины  при обработке результатов моделирования можно использовать

.

Непосредственное вычисление дисперсии по этой формуле нерационально, так как среднее значение изменяется в процессе накопления значений у_k. Это приводит к необходимости запоминания всех N значений у_k. Поэтому более рационально организовать фиксацию результатов моделирования для оценки дисперсии с использованием следующей формулы:

.

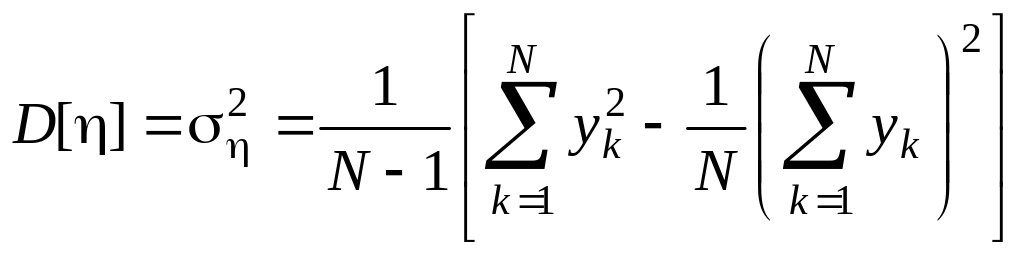Тогда для вычисления дисперсии достаточно накапливать суммы: значений y_k и их квадратов .

Для случайных величин  и  с возможными значениями x_k и y_k корреляционный момент

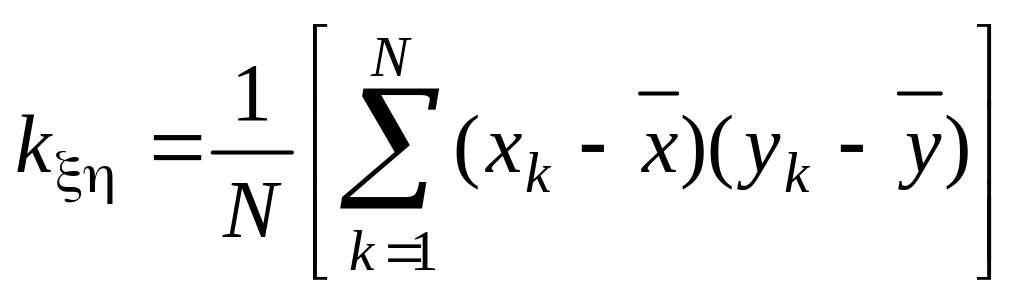или

.

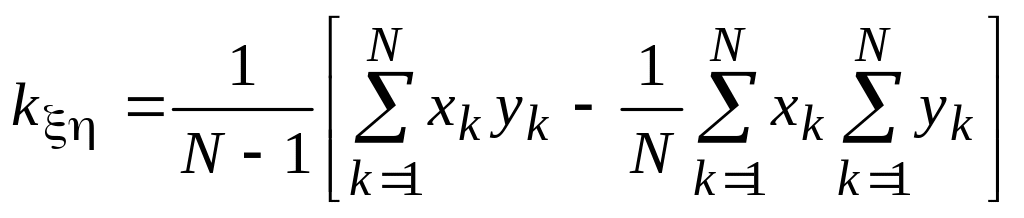Последнее выражение вычисляется при запоминании в процессе моделирования небольшого числа значений.

Если при моделировании системы S искомыми характеристиками являются математическое ожидание и корреляционная функция случайного процесса y(t) (в интервале моделирования [0,Т]), для нахождения оценок этих величин указанный интервал разбивают на отрезки с постоянным шагом t и накапливают значения процесса y_k(t) для фиксированных моментов времени t=t_m=mt.

При обработке результатов моделирования математическое ожидание и корреляционную функцию запишем так:

;

,

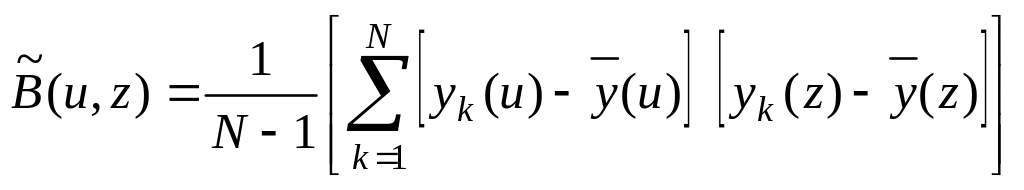где и и z пробегают все значения t_m.

Для уменьшения затрат машинных ресурсов на хранение промежуточных результатов последнее выражение также целесообразно привести к следующему виду:

.

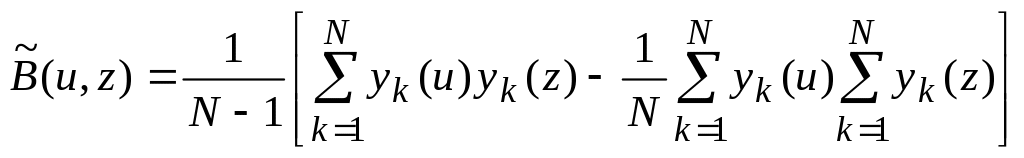Отметим особенности фиксации и обработки результатов моделирования, связанные с оценкой характеристик стационарных случайных процессов, обладающих эргодическим свойством. Пусть рассматривается процесс y(t). Тогда с учетом этих предположений поступают в соответствии с правилом: среднее по времени равно среднему по множеству. Это означает, что для оценки искомых характеристик выбирается одна достаточно продолжительная реализация процесса y(t), для которой целесообразно фиксировать результаты моделирования. Для рассматриваемого случая запишем математическое ожидание и корреляционную функцию процесса:

;

.

На практике при моделировании на ЭВМ системы S интервал (0, Т) оказывается ограниченным и, кроме того, значения y(t) удается определить только для конечного набора моментов времени t_m. При обработке результатов моделирования для получения оценок у и B() используем приближенные формулы:

;

,

которые целесообразно преобразовать к виду, позволяющему эффективно организовать порядок фиксации и обработки результатов моделирования на ЭВМ.

Задачи обработки результатов моделирования. При обработке результатов машинного эксперимента с моделью М_м наиболее часто возникают следующие задачи:

• определение эмпирического закона распределения случайной величины,

• проверка однородности распределений,

• сравнение средних значений и дисперсий переменных, полученных в результате моделирования, и т.д.

Эти задачи с точки зрения математической статистики являются типовыми задачами по проверке статистических гипотез.

Задача определения эмпирического закона распределения случайной величины наиболее общая из перечисленных, но для правильного решения требует большого числа реализаций N. В этом случае по результатам машинного эксперимента находят значения выборочного закона распределения F_э(y) (или функции плотности f_э(у)) и выдвигают нулевую гипотезу Н₀, о том, что полученное эмпирическое распределение согласуется с каким-либо теоретическим распределением. Проверяют эту гипотезу Н₀ с помощью статистических критериев согласия Колмогорова, Пирсона, Смирнова и т.д., причем необходимую в этом случае статистическую обработку результатов ведут по возможности в процессе моделирования системы S на ЭВМ.

Для принятия или опровержения гипотезы выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределения, связанную с недостаточностью статистического материала и другими случайными причинами. Закон распределения этой случайной величины зависит от закона распределения случайной величины  и числа реализации N при статистическом моделировании системы S. Если вероятность расхождения теоретического и эмпирического распределения P{U_тU} велика в понятиях применяемого критерия согласия, проверяемая гипотеза о виде распределения Н₀ не опровергается. Выбор вида теоретического распределения F(y) (или f(y)) проводится по графикам (гистограммам) F_э(y) (или f_э(y)), выведенным на печать или на экран дисплея.

Рассмотрим особенности использования при обработке результатов моделирования системы S на ЭВМ ряда критериев согласия.

Критерий согласия Колмогорова. Основан на выборе в качестве меры расхождения U величины D = max[F_э(y) – F(y)].

Из теоремы Колмогорова следует, что = D при N имеет функцию распределения

F(z) = P{<z} = , z>0.

Если вычисленное на основе экспериментальных данных значение  меньше, чем табличное значение при выбранном уровне значимости , то гипотезу H₀ принимают; в противном случае расхождение между F_э(у) и F(y) считается неслучайным и гипотеза H₀ отвергается.

Критерий Колмогорова для обработки результатов моделирования целесообразно применять в тех случаях, когда известны все параметры теоретической функции распределения. Недостаток использования этого критерия связан с необходимостью фиксации в памяти ЭВМ для определения D всех статистических частот с целью упорядочения в порядке возрастания.

Критерий согласия Пирсона. Основан на определении в качестве меры расхождения U величины

²= ,

где т_i – количество значений случайной величины , попавших в i-й подынтервал; p_i – вероятность попадания случайной величины  в i-й подынтервал, вычисленная из теоретического распределения; d – количество подынтервалов, на которые разбивается интервал измерения в машинном эксперименте.

При N закон распределения величины U, являющейся мерой расхождения, зависит только от числа подынтервалов и приближается к закону распределения ² (хи-квадрат) с (d – r – 1) степенями свободы, где r – число параметров теоретического закона распределения.

Из теоремы Пирсона следует, что, какова бы ни была функция распределения F(y) случайной величины , при N распределение величины ² имеет вид:

,

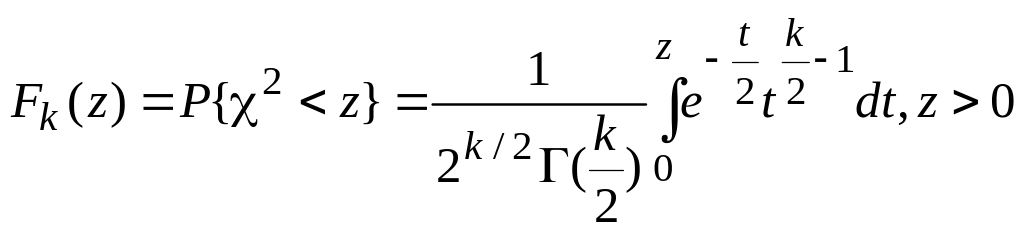где Г(k/2) – гамма-функция; z – значение случайной величины ²; k=d – r – 1 – число степеней свободы. Функции распределения F_k(z) табулированы.

По вычисленному значению U = ² и числу степеней свободы k с помощью таблиц находится вероятность P{ ²}. Если эта вероятность превышает некоторый уровень значимости , то считается, что гипотеза H₀ о виде распределения не опровергается результатами машинного эксперимента.

Критерий согласия Смирнова. При оценке адекватности машинной модели М_м реальной системе S возникает необходимость проверки гипотезы H₀, заключающейся в том, что две выборки принадлежат одной и той же генеральной совокупности. Если выборки независимы и законы распределения совокупностей F(u) и F(z), из которых извлечены выборки, являются непрерывными функциями своих аргументов u и z, то для проверки гипотезы H₀ можно использовать критерий согласия Смирнова, применение которого сводится к следующему. По имеющимся результатам вычисляют эмпирические функции распределения F_э(u) и F_э(z) и определяют

D = max |F_э(u) – F_э(z)|.

Затем при заданном уровне значимости у находят допустимое отклонение

,

где N₁ и N₂ – объемы сравниваемых выборок для F_э(u) и F_э(z), и проводят сравнение значений D и D_: если D>D_, то нулевую гипотезу H₀ о тождественности законов распределения F(u) и F(z) с доверительной вероятностью =1 –  отвергают.

Критерий согласия Стьюдента. Сравнение средних значений двух независимых выборок, взятых из нормальных совокупностей с неизвестными, но равными дисперсиями D[]=D[], сводится к проверке нулевой гипотезы Н₀:  = u – z = 0 на основании критерия согласия Стьюдента (t-критерия). Проверка по этому критерию сводится к выполнению следующих действий. Вычисляют оценку

,

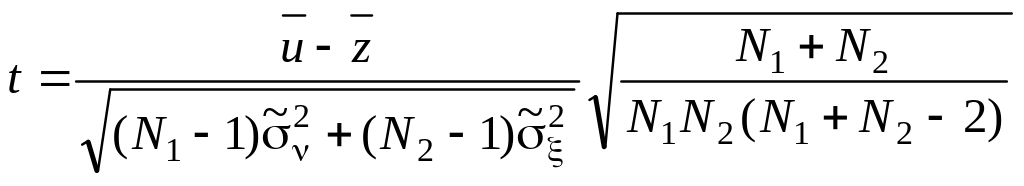где N₁ и N₂ – объемы выборок для оценки u и z соответственно; и – оценки дисперсий соответствующих выборок.

Затем определяют число степеней свободы k = N₁ + N₂ – 2, выбирают уровень значимости  и по таблицам находят значение t_. Расчетное значение t сравнивается с табличным t_ если |t| < t_, то гипотеза H₀ не опровергается результатами машинного эксперимента.

Критерий согласия Фишера. Задача сравнения дисперсий сводится к проверке нулевой гипотезы H₀, заключающейся в принадлежности двух выборок к одной и той же генеральной совокупности. Пусть необходимо сравнить две дисперсии и , полученные при обработке результатов моделирования и имеющие k₁ и k₂ степеней свободы соответственно, причем > . Для того чтобы опровергнуть нулевую гипотезу H₀: = , необходимо при уровне значимости  указать значимость расхождения между и . При условии независимости выборок, взятых из нормальных совокупностей, в качестве критерия значимости используется распределение Фишера (F-критерий) F= / , которое зависит только от числа степеней свободы k₁=N₁ – 1, k₂=N₂ – 1, где N₁ и N₂ – объемы выборок для оценки и соответственно.

Алгоритм применения критерия Фишера следующий:

1. вычисляется выборочное отношение F= / ;

2. определяется число степеней свободы k₁=N₁ – 1 и k₂=N₂ – 1;

3. при выбранном уровне значимости  по таблицам F-распределения находятся значения границ критической области ;

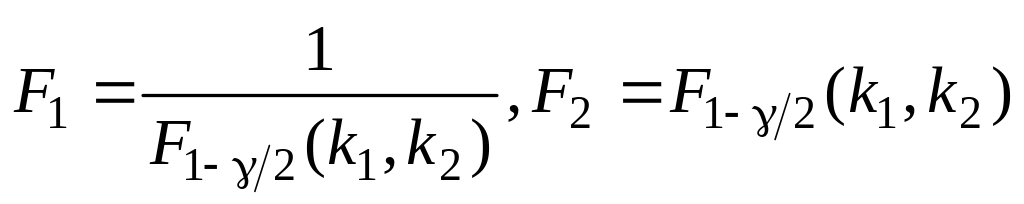4. проверяется неравенство F₁  F  F₂; если это неравенство выполняется, то с доверительной вероятностью  нулевая гипотеза H₀: = может быть принята.

Рассмотренные оценки искомых характеристик процесса функционирования системы S, полученные в результате машинного эксперимента с моделью М_м, являются простейшими и охватывают большинство случаев, встречающихся в практике обработки результатов моделирования системы для целей ее исследования и проектирования.