3.2. Методы решения дифференциальных уравнений

Само по себе дифференциальное уравнение не имеет однозначного решения. Чтобы получить его, надо помимо самого уравнения задать дополнительные условия. По типу дополнительных условий различают одноточечные и многоточечные задачи. В одноточечных задачах все условия задаются в одной точке (при одном и том же х). Обычно это начальная точка х₀. В этом случае говорят, что поставлена задача Коши.

Пример 3.1. Задача Коши:

.

В многоточечной задаче дополнительные условия задаются в нескольких точках. Часто это границы отрезка определения решения. Тогда говорят, что поставлена краевая задача.

Пример 3.2. Краевая задача:

.

Несложно убедиться, что задачи примеров 3.1 и 3.2 имеют одинаковое решение у = 1.125 е^2х – 0.125 е^{– 2х} – 2х.

Наиболее важной является задача Коши для уравнения 1-го порядка – к ней сводятся многие другие задачи.

Аналитическое решение ОДУ – это аналитически заданная функция у(х) (см. примеры 3.1 и 3.2). Численное решение – таблица значений функции у(х) в дискретных точках (в узлах). Так, численным решением задач рассмотренных примеров является таблица 3.1.

Таблица 3.1
Численное решение примеров 3.1 и 3.2
х	0	0.2	0.4	…	1.6	1.8	2.0
у	1	1.1945	1.6476	…	24.3940	37.5696	57.4206

Опишем два простейших метода получения численного решения задачи Коши для уравнения 1-го порядка. Пусть дифференциальное уравнение разрешено относительно . Имеем задачу:

. (3.1)

Все численные методы решения задачи (3.1) в качестве основного блока имеют некую процедуру вычисления значения у_i+1, если известно у_i и некоторые другие параметры. Т.е. вначале задаётся точка (х₀, у₀), по ней вычисляем точку (х₁, у₁), затем тем же способом вычисляем (х₂, у₂), и т.д. до конца таблицы.

Пусть h – шаг по х в таблице численного решения. Из определения производной имеем приближённую формулу:

. (3.2)

Согласно уравнению (3.1) . Обозначим y(x) = у_i, y(x + h) = у_i+1. Тогда из (3.2) имеем следующую расчётную формулу:

у_i+1 = у_i + hf(x, у_i). (3.3)

Полученная формула представляет собой простейший метод численного решения задачи Коши для уравнения 1-го порядка, называемый явным методом Эйлера.

Метод (3.3) является недостаточно точным и используется обычно только для каких-нибудь прикидочных расчётов. В более точном методе сначала по формуле (3.3) получают так называемое прогнозируемое значение у_i+1, которое затем уточняют:

= у_i + h f(х_i , у_i); у_i+1 = у_i + [ f(x_i, у_i ) + f(x_i + h, ) ], (3.4)

Этот метод называется модифицированным методом Эйлера, он позволяет достаточно просто получить уже весьма точное решение.

На рис. 3.3. представлены численное и аналитическое решение следующей задачи Коши:

. (3.5)

Здесь f(x, y) = y² + 1. Аналитическое решение задачи y = tg x.

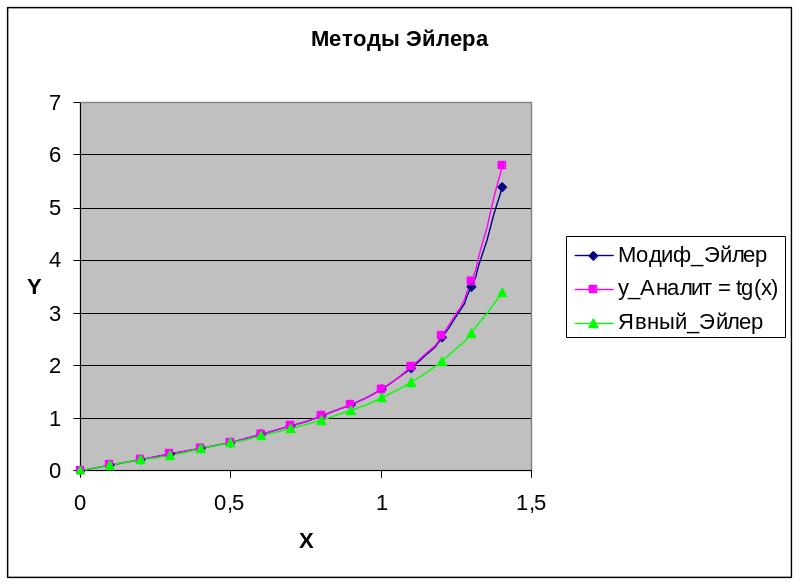
Рис. 3.3. Сравнение численного и аналитического решения задачи (3.5)

Пример. На вход аппарата идеального смешения объёма V подаётся раствор вещества концентрации с объёмным расходом u м³ / сек (Рис. 3.4). Составить модель, описывающую изменение концентрации вещества на выходе аппарата.

V

u м³ / сек

Y вх =1/(t+1)

Y

Рис. 3.4. Аппарат идеального смешения

Решение. Составим уравнение баланса количества вещества на входе и выходе аппарата за время от t до t + t. Исходное уравнение:

Q_накопл = Q_входн – Q_выходн, (3.6)

где Q_накопл = [y(t+t) – y(t)]V; Q_входн = y_вхut; Q_выходн = yut.

Разделим (2.6) на t и перейдём к пределу при t  0. Получим следующее дифференциальное уравнение

,

которое и является искомой моделью процесса. Решение этого уравнения модифицированным методом Эйлера см. файл «Теоретич_МОДЕЛИР.xls» лист «Аппарат».