Структурные схемы с нелинейными элементами

Для исследования нелинейных систем структурная схема приводится к виду:

НЭ ЛЧ

x

y

Основные методы расчета нелинейных систем

Они делятся на:

1. Точные.

Припасовывания, методы Ляпунова., фазового портрета.

2. Приближенные.

Ван-дер Поля, Пуанкаре, гармонической линеаризации,

Графоаналитические.

Метод гармонической линеаризации

Этот метод основан на использовании в системе гипотезы фильтра.

Предположим, что в незамкнутой системе существуют автоколебания, причем входная величина будет изменяться по гармоническому закону x=Asin(wt).

Если предполагать, что линейная частота системы выхода является фильтром низкой частоты (ФНЧ), то проходящий через линейную часть (ЛЧ) сигнал будет иметь только первую гармонику. Тогда законно предположить, что на выходе нелинейного элемента можно использовать только основную гармонику.

Если характеристика нелинейного элемента (НЭ) симметрична относительно начала координат , то постоянная составляющая в таком случае будет отсутствовать.

Если характеристика нелинейного элемента (НЭ) однозначна, то будет отсутствовать сдвиг фаз между входным и выходным напряжением.

Передаточная функция НЭ может быть охарактеризована в виде комплексного коэффициента передачи, равного отношению комплексов выходной и входной величины.

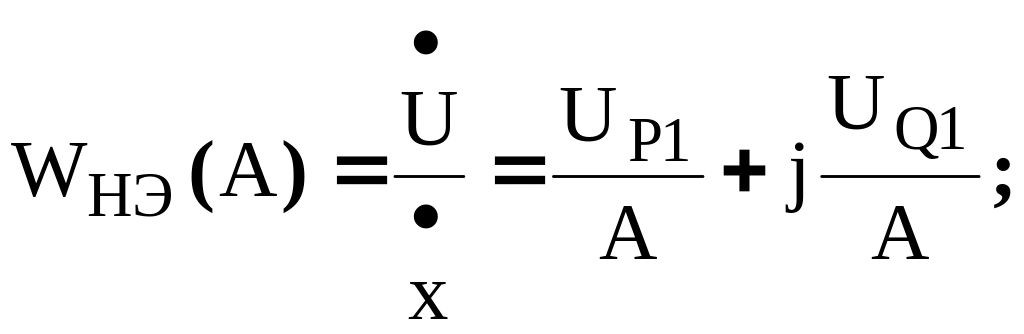(1)

В общем случае верна формула (1). Если характеристика НЭ однозначна, то

, где  коэффициенты гармоничной линеаризации, получаемые как коэффициенты разложения в ряд Фурье нелинейной функции заданного НЭ.

В книгах по ТАУ и справочниках, для любой нелинейности можно найти аналитические выражения .

Исследование автоколебаний в нелинейных системах

Метод гармоничной линеаризации позволяет решить задачу нахождения параметров автоколебаний (A и w), а также исследовать автоколебательные режимы на устойчивость.

Выведем уравнения для определения параметров автоколебаний.

 основное уравнение возникновения автоколебаний в нелинейной системе.

Решением этого уравнения получим параметры автоколебаний:

1. аналитически;

2. графоаналитически:

1. с применением АФХ;

2. с применением ЛЧХ;

3. различные модификации методов.

Метод фазовой плоскости

Фазовым называется пространство переменных состояний x₁,..,x_n. автономной системы. Автономная система предполагает, что в правые части системы дифференциальных уравнений (ДУ). Уравнения должны быть представлены в виде Коши, т.е. в них явно не входит время t ,т.е.

Это условие автономности будет выполняться при свободном движении без внешнего воздействия при нулевых начальных условиях, а также при некоторых внешних воздействиях (т.е. ступенчатом).

Сущность метода фазовой плоскости заключается в построении фазовых траекторий по ДУ в фазовом пространстве x₁,..,x_n.

Точка, определяющая состояние фазового пространства x_1i, x_2i называется изображающей.

Траектория движения изображающей точки называется фазовой траекторий.

Совокупность фазовых траекторий образует фазовый портрет.

Размерность вектора состояний x_i, определяется размерностью фазового пространства: .

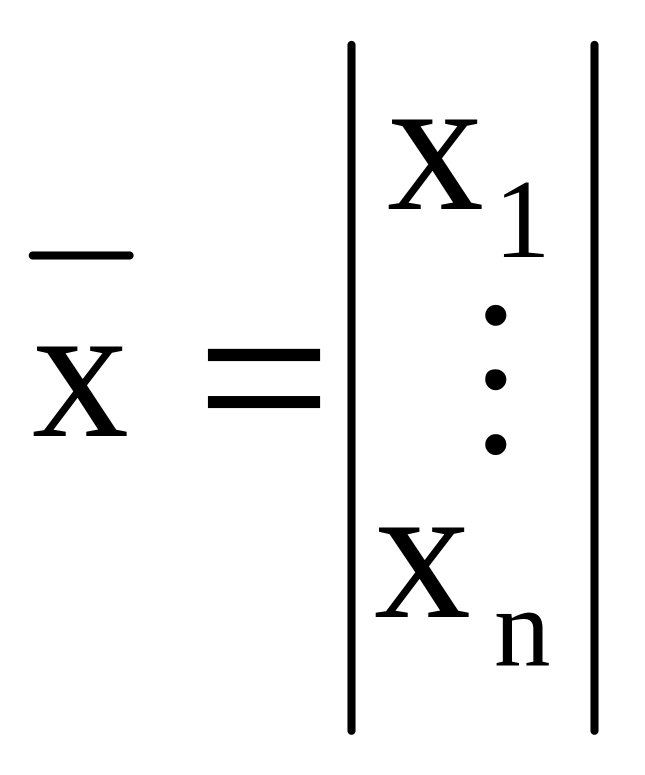Наиболее наглядно этот метод может быть представлен для системы 2-го порядка. При наличии 2-х координат, фазовое пространство превращается в фазовую плоскость.

Для системы второго порядка имеем систему уравнений в виде Коши.

Для получения ДУ в фазовой траектории, необходимо поделить уравнение (2) на (1) , тогда получим дифференциальной уравнение фазовой траектории (3).

Особенности фазовых портретов

Допустим имеем систему второго порядка, описываемую системой ДУ

, после деления второго уравнения на первое

Если функция ограничена однозначно в определенной области, то по теореме Коши имеется единственное решение этого уравнения.

Это означает:

1. Через данную точку фазовой плоскости проходит одна единственная траектория и фазовая траектория нигде не пересекается.

2)Если , то существуют особые точки, для которых  неопределена. В этих точках, фазовые траектории могут пересекаться. В этих точках не существует определенных направлений касательной к траектории, т.е. в этой точке фазовые траектории сходятся или исходят из нее.

Устойчивость особых точек

Особая точка изображает устойчивое состояние равновесия, если все фазовые траектории к ней сходятся.

3)На каждой фазовой траектории можно указать стрелкой направление движения изображающей точки на ней.

Если x₂ > 0, то x₁ всегда возрастает, а если x₂ < 0, то x₁ всегда убывает, т.е. при возрастании времени движения в верхней полуплоскости слева направо, в нижней – справа налево.

4)В точках пересечения фазовых траекторий с осью абсцисс, касательная к ним перпендикулярна (при y=0 dy/dx=oo. x(t) достигает экстремума).

5)Если фазовые траектории на плоскости стягиваются к некоторой замкнутой кривой, то в такой системе будут автоколебания, поскольку в установившемся режиме координата системы и ее производная (скорость) будут периодически изменяться. Замкнутый цикл, к которому стягиваются траектории, называется предельным циклом.

Устойчивость автоколебательных режимов.

Предельный цикл является устойчивым (автоколебания устойчивы), если фазовые траектории x₂

снаружи и и внутри наматываются на него (стремятся к нему).

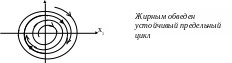
Е сли фазовые траектории снаружи и внутри расходятся от предельного цикла, то он неустойчив (автоколебания неустойчивы).

6.Фазовый портрет релейных систем имеет линии переключения. Линии переключения – это геометрическое место точек фазового пространства, в котором происходит переключение релейного элемента.

За счет введения в систему гибкой обратной связи (дифференцирующей) происходит поворот линий переключения на определенный угол, зависящий от величины коэффициента обратной связи. В этом случае в релейных системах возможна разновидность переходного процесса, называемая скользящим режимом, причем при этом повышается быстродействие (уменьшается время регулирования), исключаются автоколебания Гибкая обратная связь действует только в переходном режиме. Жесткая обратная связь действует в переходном и установившемся режиме.

Гибкая обратня связь действует более эффективно, чем жесткая.

Уравнение линии перекюлчения

Уравнение линии переключения для идеального реле x₁ = 0

Уравнение линии переключения для реле с гистерезисом

Анализ динамики нелинейных систем по фазовому портрету

По фазовому портрету можно:

1. Судить об устойчивости системы.

Если фазовые траектории сходятся к особой точке, то система устойчива. Если все фазовые траектории исходят из точки, то система неустойчива.

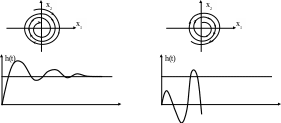
2. По фазовому портрету можно судить об устойчивости автоколебательных режимов. (см. выше)

3. По фазовой траектории можно как качественно, так и количественно построить переходной процесс.