2 Способ (способ задания частных значений):
Так как равенство (*) — тождество, то оно сохраняется при любом значении .
Будем давать
такие значения, чтобы в правой части
все члены, кроме одного, обращались в
нуль. Очевидно, такими «выгодными»
значениями являются корни знаменателя,
т. е. значения
,
,
и
.
При
в правой части (*) все слагаемые, кроме
первого, обратятся в нуль, левая часть
равенства
при
будет равна
,
и мы получим:
или
,
откуда
.
При
левая часть равна
,
а в правой части (*) все слагаемые, кроме
второго, будут равны нулю:
или
,
откуда
При в правой части (*) все слагаемые, кроме третьего, равны нулю:
или
,
откуда
.
При в правой части (*) все слагаемые, кроме четвертого, обратятся в нуль, и мы будем иметь:
или
,
откуда
.
Итак, заданная дробь может быть представлена суммой простейших дробей вида:
.
Заметим, что каким бы способом ни вычислялись неизвестные коэффициенты, мы всегда получим для них одни и те же значения, так как разложение рациональной дроби на простейшие может быть осуществлено единственным образом.
Укажем, что второй способ, способ задания частных значений , для определения неизвестных коэффициентов особенно удобен в том случае, когда знаменатель дроби содержит только действительные множители первой степени, среди которых нет равных.
В других случаях способ задания частных значений также дает сокращение вычислений, так как позволяет избежать решения системы уравнений с числом уравнений, равным числу неизвестных.
Пример.
Дробь правильная. Разобьем на множители
знаменатель дроби. Т.к. (
,
то
.
Приводя к общему знаменателю и приравнивая числители, получаем:
.
.
Сравнивая коэффициенты при одинаковых степенях в левой и правой частях последнего равенства, получаем систему четырех уравнений первой степени с четырьмя неизвестными:
Решив полученную систему, найдем значения неизвестных:
или методом Гаусса:
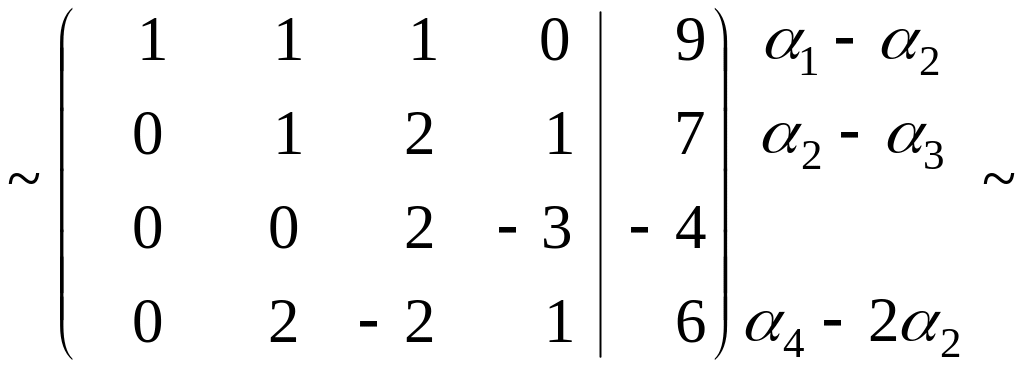
Итак,
,
,
и
.
Таким образом, вычисление исходного интеграла сводится к вычислению суммы интегралов вида:
.
Пример.
Т.к. дробь неправильная, то предварительно следует выделить из нее целую часть и правильную рациональную дробь:
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
Таким образом,
3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2)(3x – 1).
Поэтому дробь разбивается на элементарные дроби вида:
Найдем неопределенные коэффициенты методом задания частных значений. В качестве произвольных значений примем точки 3, –2, 1/3 (напомним, что при этих значениях знаменатель дроби равен нулю). Получаем:
Окончательно получаем:
=
=
Пример.
Приравняв числители левой и правой части, найдем неопределенные коэффициенты:
Сгруппируем слагаемые:
Приравнивая коэффициенты, стоящие при одинаковых степенях х, получим систему:
решение которой дает значения:
,
,
,
и
Тогда значение заданного интеграла:
.