2. Понятие о движении свободного твёрдого тела

Движение тела, при котором на перемещения его точек не накладывается никаких ограничений, называется свободным движением (или движением свободного тела).

Примеры: движение летательных аппаратов, транспортных средств, кораблей; движение брошенных мячей, камней, пушечных снарядов, спортивных снарядов (копий, ядер, дисков) и т.п.

Перемещение свободного тела можно представить как наложение поступательного перемещения вместе с полюсом и сферического перемещения вокруг полюса.

Свободное = поступательное + сферическое.

Поэтому ясно, что для того, чтобы задать движение свободного тела, надо задать поступательную часть перемещения, указав координаты полюса как функции от времени, и задать сферическую часть перемещения, определив углы Эйлера как функции от времени.

Таким образом, функции

1515\* MERGEFORMAT ()

задают закон (уравнения) движения свободного твёрдого тела.

Скорость и ускорение произвольной точки свободного тела складываются из скорости и ускорения полюса и скорости и ускорения точки при её сферическом движении вокруг полюса, т.е.

В приведённых формулах векторы – мгновенные угловые скорость и ускорение.

В заключение можно отметить, что на практике, например, в теории полёта, или в теории корабля, углы Эйлера не удобны для описания углового положения летательных аппаратов и кораблей. Поэтому применяются другие углы. Например, в авиации применяются такие углы:

3. Общие понятия сложного движения точки

Движение точки в заданной системе отсчёта может быть задано сложными уравнениями и происходить по очень сложным траекториям. Например:

.

Определение кинематических характеристик таких движений представляет сложную задачу. Для облегчения решения такой задачи и был предложен метод, который и подразумевают, когда говорят: «сложное движение точки».

Суть метода состоит в том, что, используя относительность механического движения, вводят дополнительные системы отсчёта, в которых движение точки оказывается более простым. Тогда исходное движение можно представить как наложение движений точки в дополнительно введённых системах и движении самих систем отсчёта.

Рассмотрим примеры.

1. Трубка вращается вокруг оси, а по трубке движется грузик.

Траекторией движения груза относительно неподвижной плоскости будет спираль

Если с трубкой связать систему координат, то в ней (другими словами, – относительно трубки) движение груза будет прямолинейным

При движении же груза вместе с трубкой ( в движении системы отсчета, связанной с трубкой) получим окружность

Наложение прямолинейного движения груза вдоль трубки на вращательное движение вместе с трубкой – и образует движение груза по спирали относительно неподвижной плоскости.

2. Тележка движется прямолинейно. На тележке установлен ротор, ось вращения которого вертикальна. На ободе ротора рассмотрим точку М.

Движением этой точки относительно дороги будет

Движение точки по отношению к тележке – движение по окружности

Движением точки вместе с тележкой (движение системы отсчёта, связанной с тележкой) будет прямолинейное движение:

Движение точки М относительно дороги снова образуется наложением движения точки относительно тележки и – движением вместе с тележкой.

На основании изложенных примеров можем перейти к общим понятиям и определениям.

Имеется неподвижная (основная) система координат OXYZ. Относительно неё движется как твёрдое тело (т.е. все расстояния и углы между любыми линиями не изменяются при движении) система координат oxyz. Относительно как той, так и другой систем координат движется точка М.

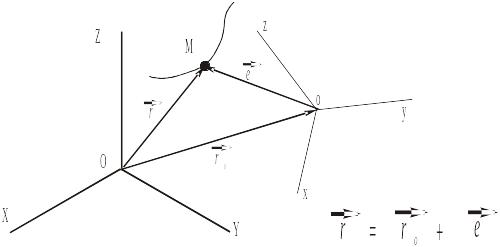
Запишем определения.

Движение, траектория, скорость и ускорение точки относительно неподвижной (основной) системы координат называются абсолютными.

В первом примере движение груза относительно неподвижной плоскости будет абсолютным, спираль – это абсолютная траектория, скорость и ускорение точки при движении по этой спирали – абсолютные скорость и ускорение точки.

Во втором примере движение точки М относительно дороги – абсолютное движение, петлеобразная кривая – абсолютная траектория.

Абсолютные скорость и ускорение обозначаются значком «а» снизу у соответствующего вектора

Движение, траектория, скорость и ускорение точки относительно подвижной системы координат называются относительными.

Первый пример: движение вдоль трубки – относительное движение, относительная траектория – прямая линия; скорость и ускорение при движении по этой прямой – относительные скорость и ускорение.

Второй пример: движение точки М вместе с ротором относительно тележки – относительное движение; относительная траектория – окружность, скорость и ускорение точки при движении по этой окружности – относительные скорость и ускорение.

Относительные скорость и ускорение обозначают значком «r» снизу у соответствующего вектора, или русскими буквами «отн»

Движение, траектория, скорость и ускорение точки вместе с подвижной системой координат относительно неподвижной называются переносными.

Первый пример: вращение груза вместе с трубкой (груз «мысленно» закрепляется на трубке и вращается вместе с ней) – переносное движение; переносные траектории – окружности; скорость и ускорение при движениям по этим окружностям – переносные скорость и ускорение.

Второй пример: прямолинейное движение точки М вместе с тележкой – переносное движение; переносная траектория – прямая линия; скорость и ускорение точки при движении по этой прямой – переносные.

На привёденном ранее рисунке

это абсолютный радиус-вектор точки М; 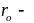абсолютный радиус-вектор точки о (начала подвижной системы координат); относительный радиус-вектор точки М.

При изучении сложного движения точки возникает ещё один вопрос: предположим, что относительный радиус-вектор точки задан как функция от времени . Можно вычислить производную от этого вектора по времени

Возникает вопрос, в какой системе отсчёта её вычислять?

Действительно, за промежуток времени изменение вектора будет различным:

в подвижной системе (в относительном движении)

изменение определено вектором , а в абсолютном движении (относительно неподвижной системы отсчёта) – вектором .

Поделив эти приращения на t и переходя к пределу при t  0, получим

Из сравнения рисунков видно, что приращения и отличаются некоторым добавочным вектором,

который образуется за счёт вращения вектора вместе с пластинкой и определяется как при вращательном движении тела.

Производную от вектора в неподвижной системе отсчёта (абсолютную производную) будем обозначать обычным образом:

1616\* MERGEFORMAT ()

Для производной в подвижной системе отсчёта (относительной производной) введём обозначение

1717\* MERGEFORMAT ()

Тогда на основании вышеизложенного, получим:

1818\* MERGEFORMAT ()

Это равенство называют формулой Бура.

Рассмотрим частные случаи формулы Бура.

1) Подвижная система движется относительно неподвижной поступательно ( ). В этом случае из (18) следует

т.е. при поступательном движении системы отсчёта производные в подвижной и неподвижной системах совпадают.

2) Вычислим производную от угловой скорости подвижной системы:

т.к. векторное произведение . Другими словами, значение производной от угловой скорости тела (системы отсчёта) не зависит от того, в какой системе координат её вычисляют: в любом случае получаем угловое ускорение.

Вывод формулы Бура может быть получен чисто математическим путём. Введём орты подвижной системы координат. Тогда относительный радиус-вектор запишется

и

Но, по формуле Эйлера (формулы Пуассона)

Слагаемые

представляют собой производную от вектора, вычисленную в предположении, что орты неподвижны, т.е. относительную производную

Оставшиеся три слагаемых преобразуем следующим образом:

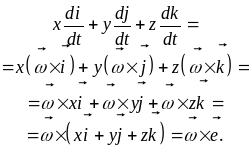
Объединяя, получаем формулу Бура.