
Пропорції
Нехай
заданий дріб
.
Він показує, що в даному числі міститься
т
п-них
частин одиниці виміру, або, розглядаючи
риску як знак ділення, у скільки разів
число т більше
або менше за п.
Наприклад, розглядаючи дріб
![]() ,
ми зазначаємо, якщо одиницю виміру
розбити на 4 рівні частини і взяти 8 таких
частин, то вони складуть 2 цілих одиниці,
тобто дріб
дорівнює числу 2. Іншими словами, він
показує, що 8 більше 4 у 2 рази. В цьому
разі дріб
розглядається як відношення 8 до 4,
значення якого дорівнює 2. Надалі,
виходячи з ідентичності позначень
ділення як дві крапки і дробової риски,
в частині випадків відношення a
: b
будемо записувати як
,
ми зазначаємо, якщо одиницю виміру
розбити на 4 рівні частини і взяти 8 таких
частин, то вони складуть 2 цілих одиниці,
тобто дріб
дорівнює числу 2. Іншими словами, він
показує, що 8 більше 4 у 2 рази. В цьому
разі дріб
розглядається як відношення 8 до 4,
значення якого дорівнює 2. Надалі,
виходячи з ідентичності позначень
ділення як дві крапки і дробової риски,
в частині випадків відношення a
: b
будемо записувати як
![]() .
.
Якщо розглядати відношення величин, то треба спиратись на такі властивості:
1) відношення величин можна замінити відношенням чисел, що їм відповідають. Наприклад, нехай нам задані два відрізка довжиною 12м і 4м. Відношення 12м : 4м = 3, тобто перший відрізок у 3 рази більший за другий. Відношення чисел 12 : 4 теж дорівнює 3, тому відношення 12м : 4м можна замінити просто відношенням чисел 12 : 4, тобто 12м : 4м = 12 : 4;
2) відношення a : b не зміниться, якщо обидва члени його помножити або поділити на одне і те ж число. Дійсно, згідно з властивістю ділення, що якщо ділене і дільник помножити або розділити на одне і те ж число, то частка не зміниться, можна записати: a : b = am : bm. Аналогічно a : b = (a:m) : (b:m). Це означає, що відношення великих чисел можна замінити відношенням малих чисел, наприклад, 36 : 48 = 3 : 4;
3)
На тій же підставі можна замінити
відношення дробових чисел цілими.
Дійсно,
:
![]() =
=
![]() :
:
![]() = ad
: bc.
Очевидно, якщо відношення
=
n
i
=
n,
то можна записати, що
=
.
= ad
: bc.
Очевидно, якщо відношення
=
n
i
=
n,
то можна записати, що
=
.
Означення: Рівність двох відношень називається пропорцією.
Якщо обидві частини цієї рівності помножити на добуток bd, то одержимо рівність ad = bc. Тобто, добуток крайніх членів пропорції дорівнює добутку середніх членів пропорції. Цей висновок одержав назву основної властивості пропорції.
Відношення бувають прямо пропорційними і зворотно пропорційними.
Відношення
називається прямо пропорційним, якщо
збільшення (зменшення) однієї величини
тягне за собою збільшення (зменшення)
у стільки ж разів другої величини.
Наприклад, 3 метри тканини коштують 9
гривень. Скільки коштують 6 метрів? 3 : 6
= 9 : х.
х =
![]() .
Тобто збільшення кількості матерії
удвічі тягне за собою і збільшення
вартості удвічі.
.
Тобто збільшення кількості матерії
удвічі тягне за собою і збільшення
вартості удвічі.
Відношення
називається зворотно пропорційним,
якщо збільшення (зменшення) однієї
величини тягне за собою зменшення
(збільшення) у стільки ж разів другої
величини. Наприклад, на 36 гривень закупили
3 м
матерії ціною по 12 гривень за метр.
Скільки метрів матерії можна закупити
на ті ж гроші ціною по 4 гривні? 3 : х
= 4 : 12. х
=
![]() ,
тобто зменшення ціни у 3 рази тягне за
собою збільшення у 3 рази кількості
матерії, яку можна закупити на ту ж суму.
,
тобто зменшення ціни у 3 рази тягне за
собою збільшення у 3 рази кількості
матерії, яку можна закупити на ту ж суму.
У наведених прикладах розглянута пропорційна залежність між двома величинами (кількість і вартість, або кількість і ціна). В цьому разі пропорція називається подвійною. Пропорційна залежність між трьома величинами називається потрійною. Прикладом її може бути залежність, викладена у задачі: 12 автомобілів на 100 км витрачають 120 л бензину. Скільки бензину витратять 16 автомобілів на 150 км?
В п р а в и.
Замінити відношення дробових чисел відношеннями цілих чисел:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
3
; г)
3![]() .
.
Концентрацією розчину називається відношення кількості розчиненої речовини до кількості усього розчину. У 2л води розчинено 40г солі. Знайти концентрацію розчину.
Концентрація розчину солі
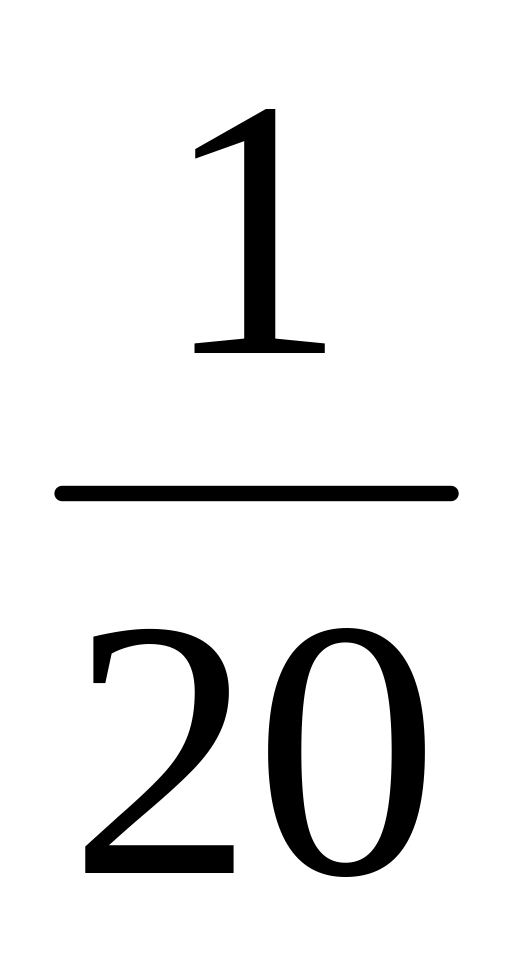 .
Скільки солі міститься у 4 л
солі?
.
Скільки солі міститься у 4 л
солі?Знайти чисельний масштаб, якщо 1см на кресленні відповідає 7 м на місцевості.
Яким відрізком на карті відобразиться відстань у 600 м на місцевості, масштаб карти а)
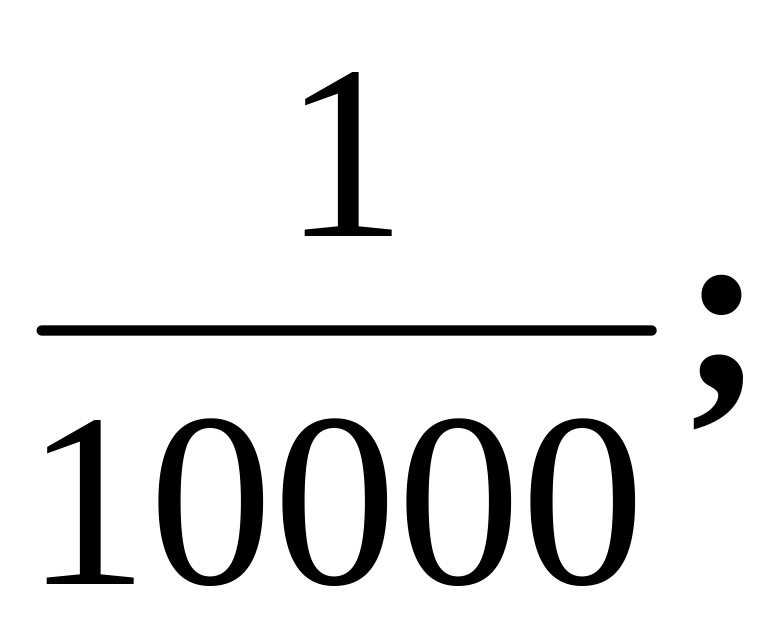 б)
б)
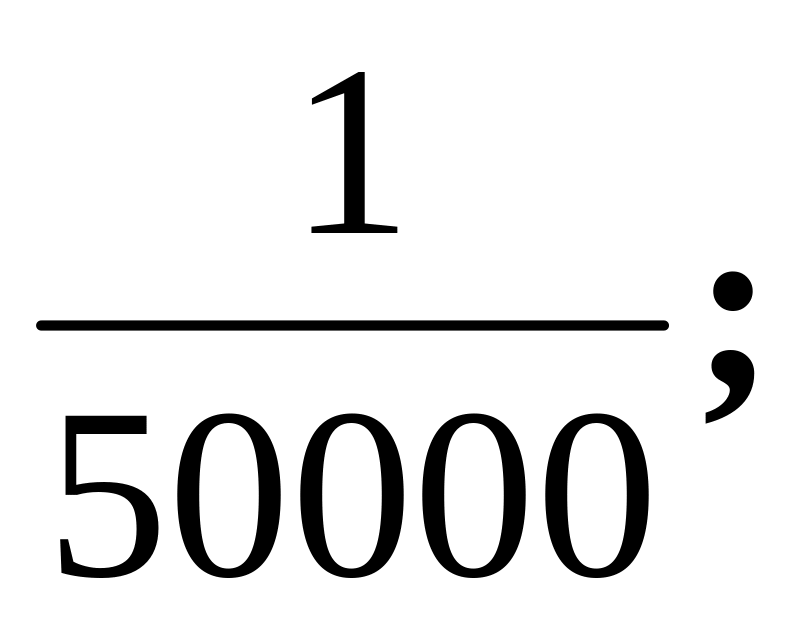 в)
в)
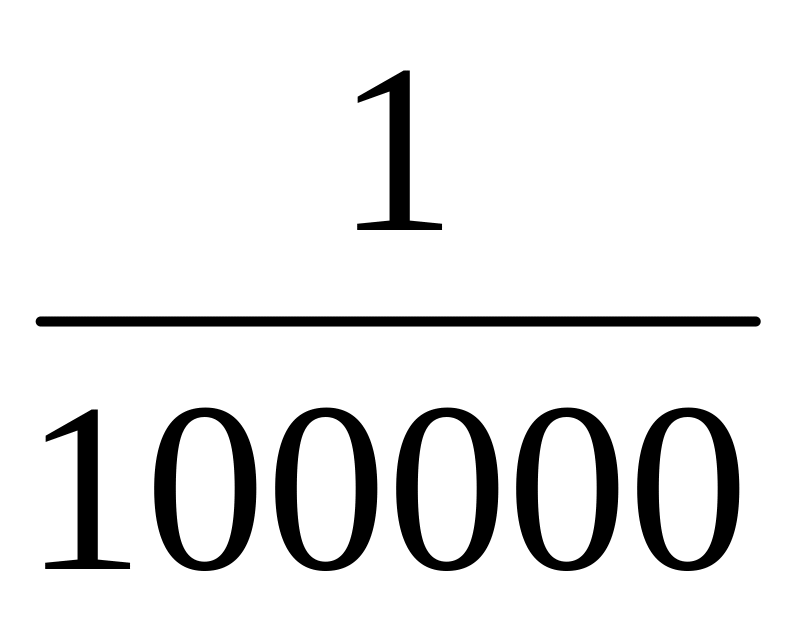 ?
?Розв’яжіть пропорції:
а) 24 : х = 8 : 5; б) х : 15 = 8 : 24; в) 343 : 98 = х : 60.
У 800 г розчину міститься 50 г солі. Скільки солі у 240 г розчину?
8. З 24 кг соняшникового насіння отримано 8 кг масла. Скільки насіння потрібно для отримання 15 кг масла?
9. На дільниці залізничної дороги замінили рейки довжиною 8 м на нові, довжиною 12 м . Скільки потрібно нових рейок на заміну 360 старих рейок.
10.Скільки обертів зробить зубчате колесо з 48 зубцями, якщо зціплене з ним колесо має 18 зубців і робить 60 обертів?
Для 16 голів худоби на 36 днів потрібно 1920 кг соломи. Скільки соломи потрібно для 20 голів худоби на 40 днів?
За 18 днів бригада лісорубів з 15 чоловік заготувала 972 куб.м деревини. Скільки деревини заготує бригада з 12 чоловік за 25 днів?
ДОДАВАННЯ В МНОЖИНІ ДОДАТНІХ РАЦІОНАЛЬНИХ ЧИСЕЛ
Означення.
Додаванням
додатних раціональних дробів називається
бінарна алгебраїчна операція “+”, яка
кожній парі дробів
і
ставить у
відповідність єдиний дріб
![]() .
.
З цього означення випливає два випадки:
1)
b = d.
У цьому разі ми маємо два дроби з
однаковими знаменниками
і
![]() тоді їх сума буде виглядати
тоді їх сума буде виглядати
![]() або
або
![]() .
Тобто,
.
Тобто,
Правило. Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники, залишивши той же знаменник.
2) b d. Тоді сума дробів має вигляд, представлений в означенні. З нього випливає і відповідне правило:
Правило. Щоб додати два звичайних дроби з різними знаменниками, треба звести їх до спільного знаменника, додати чисельники і підписати той же спільний знаменник. Якщо можна, то одержаний дріб скоротити.
З
правила додавання дробів легко випливає,
що операція додавання комутативна,
асоціативна і монотонна.
Дійсно, операція додавання комутативна,
тому що сама дія додавання виконується
з чисельниками, які являють собою цілі
числа. А для цілих чисел додавання
комутативне. Аналогічно виглядає і
доведення асоціативності. Монотонність
додавання раціональних чисел виглядає
так: якщо
![]()
![]() i
i
![]() будь-яке раціональне число, то
будь-яке раціональне число, то
![]() =
=
![]() .
Дійсно, якщо задані дроби рівні, то ad
= bc. Розглянемо,
що буде, якщо до обох частин рівності
додамо дріб
.
В результаті додавання за правилом
додавання дробів в лівій частині одержимо
дріб
.
Дійсно, якщо задані дроби рівні, то ad
= bc. Розглянемо,
що буде, якщо до обох частин рівності
додамо дріб
.
В результаті додавання за правилом
додавання дробів в лівій частині одержимо
дріб
![]() , а в правій -
, а в правій -
![]() .
Якщо за правилом порівняння дробів
перемножимо чисельник першого дробу
на знаменник другого, а знаменник першого
- на чисельник другого, то одержимо такі
два вирази: (ап
+ bm)·dn = adn2
+ bmdn, і (cn
+ dm)·bn = bcn2
+ bmdn. Порівнюючи
ці два вирази за властивістю монотонності
додавання в множині натуральних чисел,
відмічаємо, що вони рівні, оскільки
мають однакові доданки bmdn,
а bcn2
= adn2,
оскільки за умовою ad
= bc. А значить,
=
.
Якщо за правилом порівняння дробів
перемножимо чисельник першого дробу
на знаменник другого, а знаменник першого
- на чисельник другого, то одержимо такі
два вирази: (ап
+ bm)·dn = adn2
+ bmdn, і (cn
+ dm)·bn = bcn2
+ bmdn. Порівнюючи
ці два вирази за властивістю монотонності
додавання в множині натуральних чисел,
відмічаємо, що вони рівні, оскільки
мають однакові доданки bmdn,
а bcn2
= adn2,
оскільки за умовою ad
= bc. А значить,
=
![]() .
Аналогічно доводиться, що коли
.
Аналогічно доводиться, що коли
![]() >
,
то
>
,
а коли
<
,
то
<
.
>
,
то
>
,
а коли
<
,
то
<
.
ВІДНІМАННЯ В МНОЖИНІ РАЦІОНАЛЬНИХ ЧИСЕЛ
Означення.
Відніманням звичайних дробів називається
бінарна алгебраїчна операція “-“, яка
будь-якій парі дробів
і
ставить у відповідність єдиний дріб
![]() такий, що має місце рівність
такий, що має місце рівність
![]() .
.
Аналізуючи
це означення можна сказати, що віднімання
звичайних дробів є операція, за допомогою
якої за відомою сумою і одним доданком
знаходиться другий доданок. Тобто, якщо
+
![]() =
,
то
=
-
=
,
то
=
-
Теорема.
Різниця
-
в множині додатних раціональних чисел
існує тільки тоді, коли
![]() .
Дійсно, якщо
,
то ad
bc, а тому
існує різниця ad
- bc. Покажемо,
що дріб
.
Дійсно, якщо
,
то ad
bc, а тому
існує різниця ad
- bc. Покажемо,
що дріб
![]() =
є різницею
-
.
Для цього достатньо показати, що сума
+
=
.
Дійсно, за правилом додавання дробів з
різними знаменниками маємо:
+
=
+
=
є різницею
-
.
Для цього достатньо показати, що сума
+
=
.
Дійсно, за правилом додавання дробів з
різними знаменниками маємо:
+
=
+![]() =
=
=
=
![]() =
,
що і треба було одержати. Тому
=
,
що і треба було одержати. Тому
![]() -
=
.
Звідси випливає п
р а в и л о:
Щоб відняти
один звичайний дріб від другого, треба
привести їх до спільного знаменника,
відняти чисельники і підписати спільний
знаменник. Якщо можна, то результат
скоротити.
-
=
.
Звідси випливає п
р а в и л о:
Щоб відняти
один звичайний дріб від другого, треба
привести їх до спільного знаменника,
відняти чисельники і підписати спільний
знаменник. Якщо можна, то результат
скоротити.
В п р а в и.
Заданий дріб
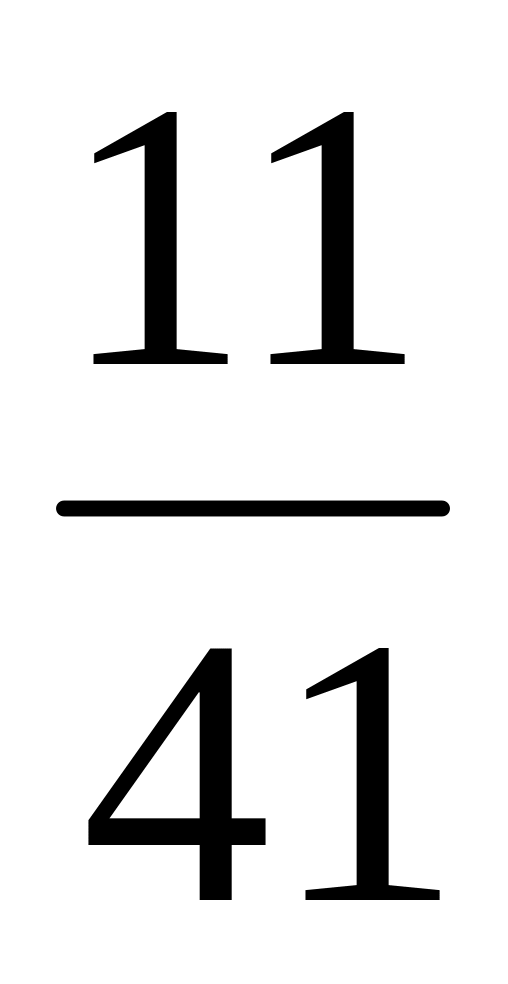 .
Яке число треба додати до чисельника
і знаменника, щоб отримати дріб
?
.
Яке число треба додати до чисельника
і знаменника, щоб отримати дріб
?Заданий дріб
 .
Яке число треба відняти з чисельника
та знаменника, щоб отримати дріб
.
Яке число треба відняти з чисельника
та знаменника, щоб отримати дріб
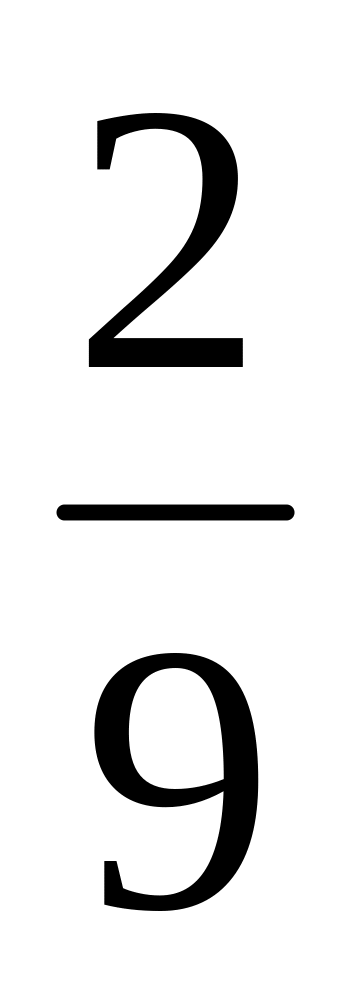 ?
?Обчислити:
а)
![]()
б)
![]() ;
;
в)
![]()
МНОЖЕННЯ ЗВИЧАЙНИХ ДРОБІВ
Означення.
Множенням
звичайних дробів називається бінарна
алгебраїчна операція, яка будь-якій
парі звичайних дробів
і
ставить у
відповідність єдиний дріб
![]() .
.
Як бачимо, чисельник і знаменник добутку дробів представляє собою добуток чисельників і знаменників цих дробів.
Множення дробів з теоретико-множинних позицій розглядається у два етапи.
1.
Розглянемо спочатку множення
звичайного дробу на ціле число,
тобто
.
с.
Це множення можна розглядати як суму с
однакових доданків виду
,
тобто
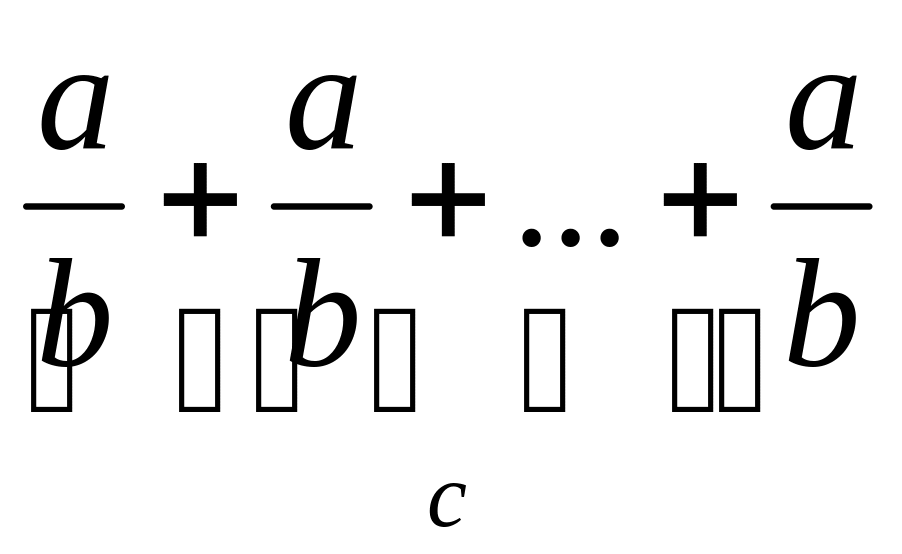 .
Тому сума буде виглядати як
.
Тому сума буде виглядати як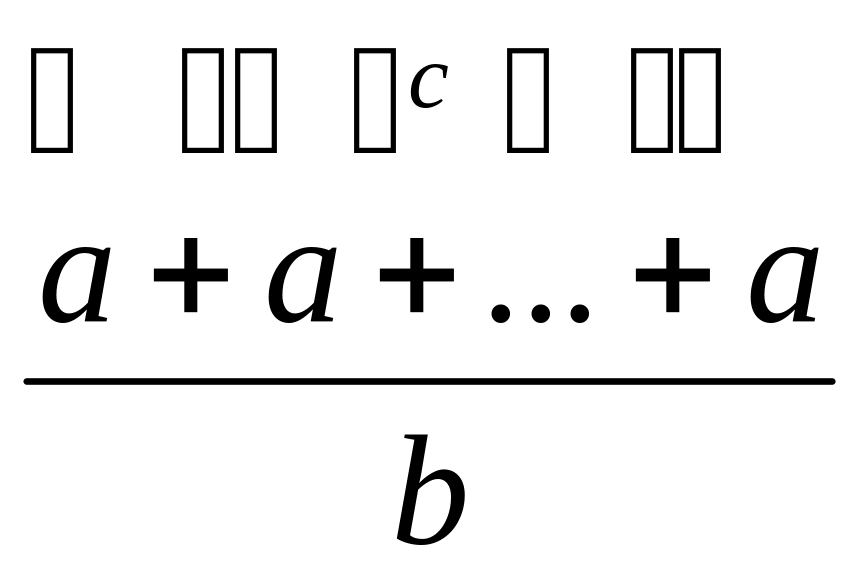 ,
де доданок а
повторюється с
разів. Тоді добуток
·
с
=
,
де доданок а
повторюється с
разів. Тоді добуток
·
с
=
![]() .
Тобто, щоб
помножити дріб на ціле число, треба
помножити на ціле число чисельник і
підписати той же знаменник. Якщо можна,
то скоротити.
.
Тобто, щоб
помножити дріб на ціле число, треба
помножити на ціле число чисельник і
підписати той же знаменник. Якщо можна,
то скоротити.
2.
Множення
дробу на дріб.
Розглянемо цю операцію на прикладі
вимірювання відрізків. Нехай заданий
відрізок
а сумірний
з одиничним відрізком
е1,
а відрізок е1
сумірний з відрізком е2,
причому довжина відрізка а
виражена мірою:
а =
![]() e1,
a е1
=
e1,
a е1
=
![]() e2.
Або
na
=
pe1,
a qe1
=
te2
.
Помноживши обидві частини першої
рівності на q,
а другої на р,
одержимо
(nq)a
= (pq)
e1
i (pq)
e1
=
(pt)e2.
Тоді за властивістю транзитивності
рівності випливає рівність: (nq)a
= (pt)e2,
а звідси випливає: а
=
e2.
Або
na
=
pe1,
a qe1
=
te2
.
Помноживши обидві частини першої
рівності на q,
а другої на р,
одержимо
(nq)a
= (pq)
e1
i (pq)
e1
=
(pt)e2.
Тоді за властивістю транзитивності
рівності випливає рівність: (nq)a
= (pt)e2,
а звідси випливає: а
=
![]() e2.
Тобто, довжина відрізка а
буде виражатися звичайним дробом
.
З другого боку, оскільки
а =
e2.
Тобто, довжина відрізка а
буде виражатися звичайним дробом
.
З другого боку, оскільки
а =
![]() e1,
а е1
=
e2,
то, підставивши в а
замість
е1
його вираз
через е2,
одержимо, що а
=
e1,
а е1
=
e2,
то, підставивши в а
замість
е1
його вираз
через е2,
одержимо, що а
=
![]() е2.
Звідси
=
.
е2.
Звідси
=
.
Правило: Щоб перемножити два звичайних дроби, треба окремо перемножити чисельники і знаменники.
Множення звичайних дробів має властивості комутативності, асоціативності та скорочуваності. Дійсно, для будь-яких цілих чисел а, b і с маємо аb = bа, (аb)с = а(bс), а з ас = bс випливає, а = b.
Спираючись
на алгоритм множення, що випливає з
означення, ми відмічаємо, що
=
![]() ,
а
=
,
а
=
![]() .
Але у чисельнику і у знаменнику ми маємо
дії з цілими числами, для яких комутативний
закон виконується, тобто
=
,
а значить
=
.
.
Але у чисельнику і у знаменнику ми маємо
дії з цілими числами, для яких комутативний
закон виконується, тобто
=
,
а значить
=
.
Аналогічно доводиться і асоціативність множення.
Крім того, множення в множині Q дистрибутивне відносно додавання і монотонне, тобто для будь-яких трьох чисел а, b і с з мн. Q (числа a, b i c представляють три звичайні дроби) має місце рівність: (а + b)с = ас + bс, а з а > b випливає ас >bс.
ДІЛЕННЯ ЗВИЧАЙНИХ ДРОБІВ
Означення.
Діленням звичайних дробів називається
бінарна логічна операція, яка будь-яким
двом дробам
і
ставиться
у відповідність єдине число
![]() таке, що
=
.
таке, що
=
.
Порівняння операцій
множення і ділення показує, що ділення
на
можна замінити множенням
на
![]() .
Тому операція ділення вважається
оберненою до множення, тобто це дія, за
допомогою якої за відомим добутком і
відомим одним співмножником знаходять
невідомий другий співмножник. Або: якщо
=
,
то
:
=
.
.
Тому операція ділення вважається
оберненою до множення, тобто це дія, за
допомогою якої за відомим добутком і
відомим одним співмножником знаходять
невідомий другий співмножник. Або: якщо
=
,
то
:
=
.
Теорема. Ділення дробових чисел завжди виконується.
Дійсно,
з того, що
=
,
випливає
![]() =
,
або cbx= ady.
Звідси випливає х
=
=
,
або cbx= ady.
Звідси випливає х
=
![]() ,
або
=
,
або
=
![]() .
Тобто п р
а в и л о: щоб
розділити дріб на дріб, треба чисельник
першого дробу помножити на знаменник
другого і результат записати в чисельник,
а знаменник першого дробу помножити на
чисельник другого і записати у знаменник.
Якщо можна, то зробити скорочення.
.
Тобто п р
а в и л о: щоб
розділити дріб на дріб, треба чисельник
першого дробу помножити на знаменник
другого і результат записати в чисельник,
а знаменник першого дробу помножити на
чисельник другого і записати у знаменник.
Якщо можна, то зробити скорочення.
Означення.
Числом,
оберненим числу
,
називається число
![]() (зважаючи,
що а
0 і b
0).
(зважаючи,
що а
0 і b
0).
Теорема. При множенні будь-якого раціонального числа на правильний дріб одержується число менше за задане.
Дійсно,
нехай задані раціональне число
і правильний дріб
,
де т <
n.
Виконаємо множення
=
![]() .
Порівняємо дроби
і
.
Маємо добутки аbп
і аbт. Виходячи
з властивості монотонності очевидно,
що аbп >
аbт,
а це свідчить, що
>
.
.
Порівняємо дроби
і
.
Маємо добутки аbп
і аbт. Виходячи
з властивості монотонності очевидно,
що аbп >
аbт,
а це свідчить, що
>
.
В п р а в и.
Виконайте обчислення:
a)
![]() ;
б)
;
б) 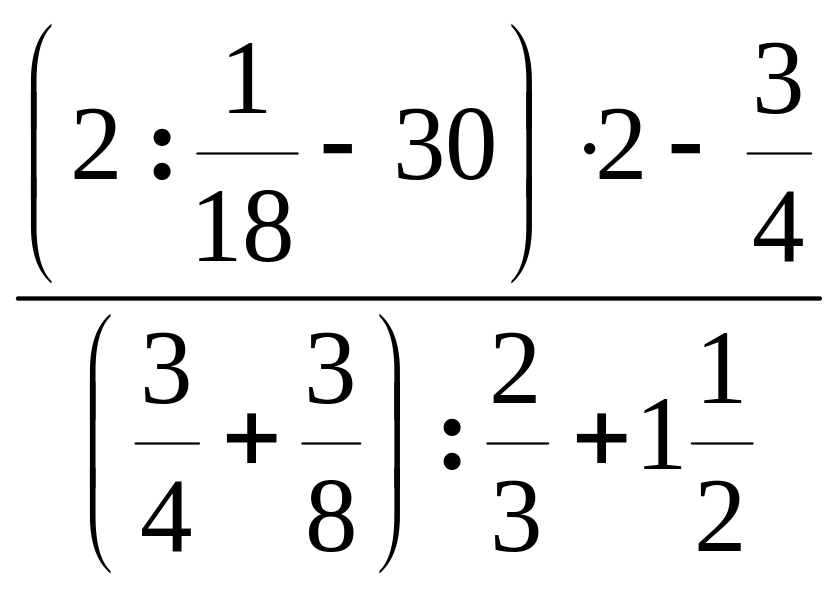 .
.
Розв’яжіть рівняння:
а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
;
г)
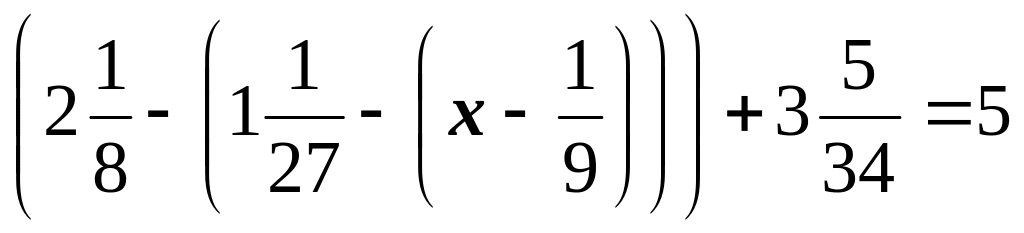 ; д)
; д)
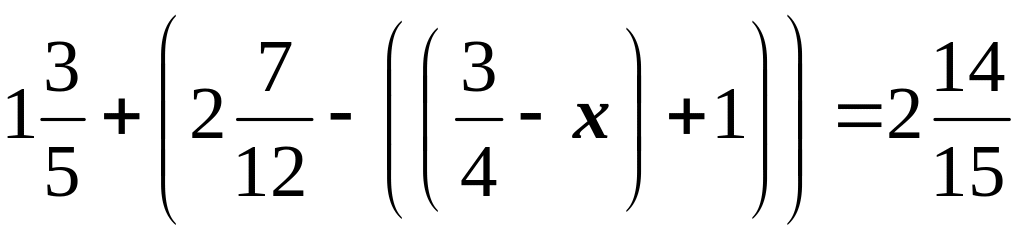 ;
;
є)
![]() .
.
Автозавод випустив три партії машин. Кількість машин першої партії складають
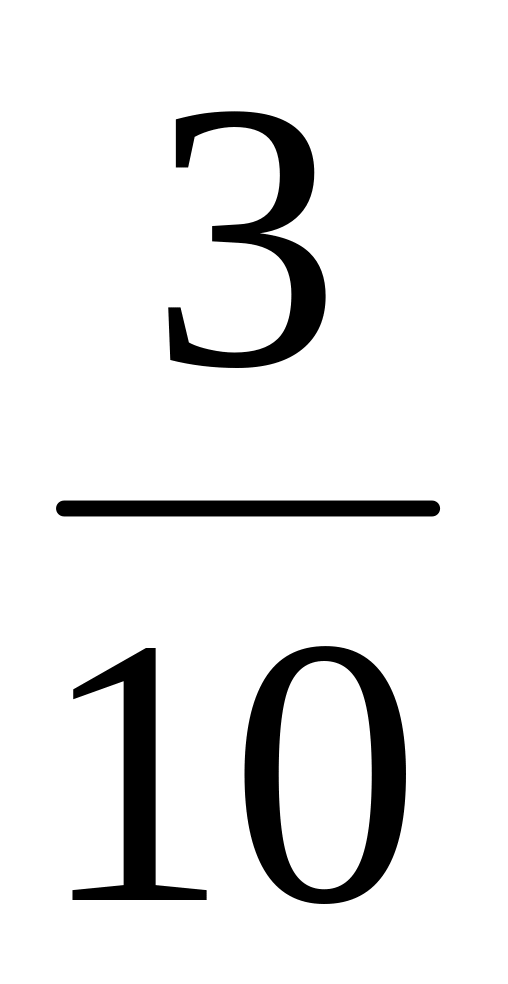 усіх випущених автомобілів. У другій
партії кількість машин в 1
усіх випущених автомобілів. У другій
партії кількість машин в 1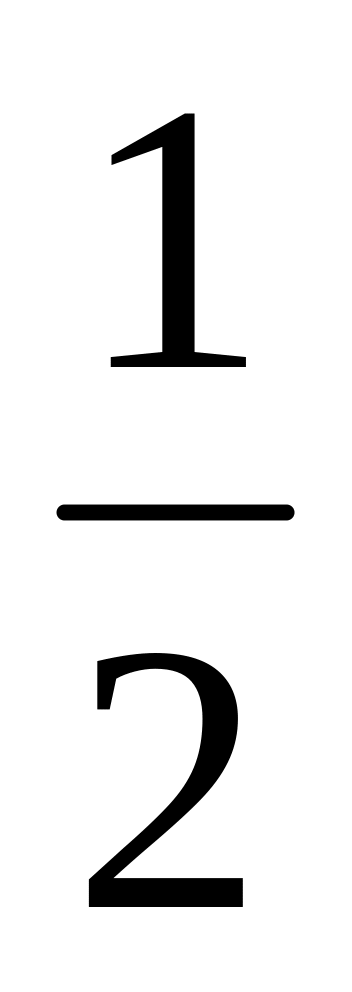 разів більше, ніж у першій. А в третій
партії на 420 машин менше, ніж у другій.
Скільки всього машин випустив завод?
разів більше, ніж у першій. А в третій
партії на 420 машин менше, ніж у другій.
Скільки всього машин випустив завод?Три шматки заліза мають загальну масу 17
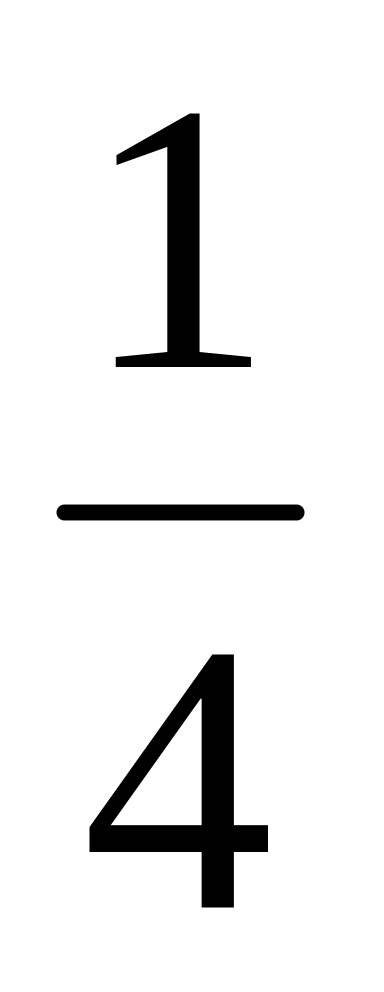 кг.
Якщо масу першого шматка зменшити на
1
кг,
а масу другого на 2
кг,
то усі три шматки будуть мати однакову
масу. Якої маси був кожний шматок?
кг.
Якщо масу першого шматка зменшити на
1
кг,
а масу другого на 2
кг,
то усі три шматки будуть мати однакову
масу. Якої маси був кожний шматок?Суміш з води та цукру має масу 330г. Маса цукру в цієї суміші складає
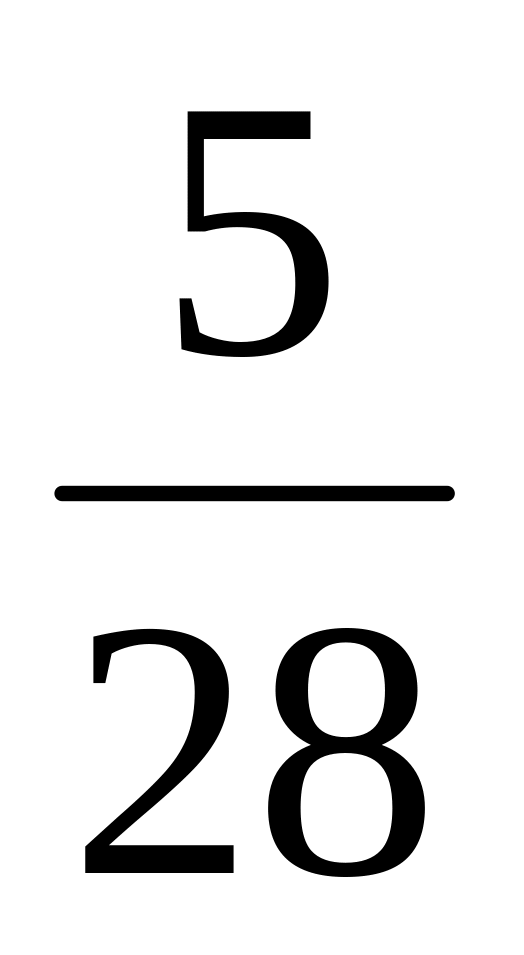 маси води. Скільки в суміші цукру і
скільки води?
маси води. Скільки в суміші цукру і
скільки води?
ВІДНОШЕННЯ ПОРЯДКУ НА МНОЖИНІ
РАЦІОНАЛЬНИХ ЧИСЕЛ
З
порівняння дробів
і
![]() випливає, що між будь-якими двома
раціональними числами можна встановити
одне з трьох відношень:
<
,
>
або
=
.
випливає, що між будь-якими двома
раціональними числами можна встановити
одне з трьох відношень:
<
,
>
або
=
.
Теорема. В множині раціональних чисел виконується властивість транзитивність нерівності. Тобто треба довести, що коли < , а < , то < . Дійсно, якщо < , то ad < bc, а якщо < , то cn < dm. Перемноживши ці дві нерівності, одержимо нерівність adcn < bcdm, або an < bm, а це означає, що < . Що і треба було довести.
Теорема. Відношення нерівності асиметричне. Дійсно, нехай задана нерівність < . Тоді вірним буде ad < bc. Але за властивістю асиметричності в множині цілих чисел невірним буде bc < ad, тобто невірною буде і нерівність < , тобто відношення нерівності асиметричне.
З цих двох теорем випливає наслідок, що на множині раціональних чисел визначене відношення порядку.
Окрім названої властивості раціональних чисел, множина Q має і такі важливі властивості як щільність та зчисленість.
Означення. Множина М називається щільною, якщо між будь-якими двома якомога близько розташованими елементами існує ще нескінчена кількість елементів.
Теорема. Множина раціональних чисел щільна.
Нехай
задані два раціональних числа а
і
b. Для них
завжди існує їх середнє арифметичне
![]() ,
тобто число, що знаходиться між ними.
А оскільки ці числа будь-які, то це
означає, що які б не були раціональні
числа а і
b, між ними
завжди міститься ще нескінченна
кількість раціональних чисел.
,
тобто число, що знаходиться між ними.
А оскільки ці числа будь-які, то це
означає, що які б не були раціональні
числа а і
b, між ними
завжди міститься ще нескінченна
кількість раціональних чисел.
Означення. Множина називається зчисленною, якщо між її елементами і множиною натуральних чисел можна встановити взаємно-однозначну відповідність. Якщо такої відповідності встановити не можна, то множина називається незчисленною.
Теорема. Множина раціональних чисел зчисленна.
Щоб
це довести, введемо попередні умови:
представимо кожне раціональне число у
вигляді звичайного дробу. Назвемо
висотою дробу суму його чисельника і
знаменника. Розташуємо всі звичайні
дроби в порядку зростання висоти, а
числа з однією висотою - в порядку
зростання чисельника. Цей ряд буде
мати такий вигляд:
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
... Таким методом можна перебрати,
перелічити всі звичайні дроби, тобто
поставити їм у відповідність множину
натуральних чисел.
,
... Таким методом можна перебрати,
перелічити всі звичайні дроби, тобто
поставити їм у відповідність множину
натуральних чисел.
Q+
=
![]() ,
,
,
,
,
,
...
,
,
,
,
,
,
...![]()
↕ ↕ ↕ ↕ ↕ ↕ ↕
N = {1 2 3 4 5 6 7 … }
А це означає, що множина раціональних чисел зчисленна.
