2.4. Средние отклонения от средних величин

Каждая статистическая величина от среднего значения отличается (отклоняется) по-разному и в любую сторону: со знаком плюс или ми­нус. Поэтому для оценки типичности полученной средней величины надо знать величину среднего отклонения совокупности от нее. По­скольку неизбежны и отрицательные отдельные отклонения, необходи­ма нейтрализация знака минус, иначе среднего отклонения не получит­ся. Этого можно достичь двумя способами: принять отрицательные от­клонения по модулю или возвести их во вторую степень (в квадрат).

При первом способе образуется среднее линейное отклонение, а при втором — среднее квадратическое. В связи с тем, что средние величины могут быть простыми и взвешенными, аналогичными могут быть и средние отклонения. Поэтому среднее линейное отклонение определяет­ся по формулам

– простое; (1.22)

– взвешенное. (1.23)

В этих формулах прямые скобки означают, что разности или откло­нения берутся по модулю, то есть без учета знака. Если ошибочно вме­сто прямых скобок принять обычные круглые, то получится Л=0.

При использовании второго способа вначале определяется дисперсия отклонений по формулам

– простая; (1.24)

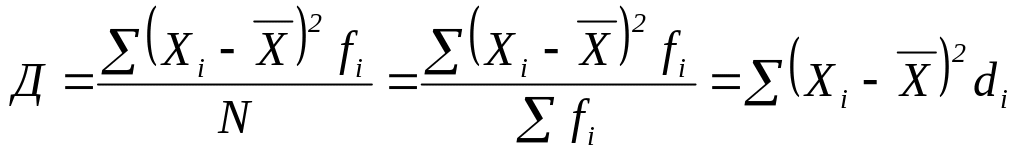– взвешенная.(1.25)

В отличие от математики статистика оперирует не абстрактными, а смысловыми величинами, имеющими размерность. Поэтому и диспер­сия здесь не безразмерная, как в математике, а сопровождается квадратической размерностью. Например, если статистическая величина измеряется в годах, или рублях, то дисперсия отклонений получится в «квадратных» годах или в «квадратных» рублях.

Для получения обычной размерности находится среднее квадратическое отклонение («сигма») как корень квадратный из дисперсии. То есть

= . (1.27)

Однако значения средних отклонений, как любой абсолютной вели­чины, служат лишь количественной мерой анализа статистической со­вокупности. Для качественного анализа применяются относительные критерии, называемые коэффициентами вариации.

2.7. Коэффициенты вариации

Вариация — это несовпадение значений одной и той же статистиче­ской величины у разных объектов в силу особенностей их собственного развития, а также различия условий, в которых они находятся. Вариация имеет объективный характер и помогает познать сущность изучаемого явления. Если средняя величина сглаживает индивидуальные различия, то вариация, наоборот, их подчеркивает, устанавливая типичность или не типичность найденной средней величины для конкретной статистической совокупности. Вариация измеряется с помощью относительных величин, называе­мых коэффициентами вариации и определяемых в виде отношения среднего отклонения к средней величине.

Поскольку среднее отклоне­ние может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации. Следова­тельно, коэффициенты вариации надо определять по формулам

– линейный; (1.28)

– квадратический. (1.29)

Значения коэффициента вариации изменяются от 0 до 1 и чем ближе он к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности, а значит и качественнее подобраны статистические данные. При этом критериальным значением коэффициен­та вариации служит 1/3.

То есть средняя величина считается типичной для данной совокуп­ности при λ 0,333 или при ν 0,333. В ином случае средняя величина не типична и требуется пересмотреть статистическую совокупность с целью включения в нее более объективных статистических величин.

С помощью линейного коэффици­ента вариации принципиальный вывод о типичности или не типичности средней величины можно получить проще и быстрее, чем с помощью квадратического. Однако квадратический коэффициент применяется чаще, так как существует несколько способов для вычисления дисперсии.

Поэтому возможен дополнительный анализ статистической сово­купности с помощью коэффициента осцилляции, определяемого по формуле

, (1.30)

где R — размах вариации в виде разности наибольшего и наимень­шего значений в совокупности статистических величин. То есть R = Х_мах –Х_min, (1.31)

где X_мax и X_min — максимальное и минимальное значения в совокупно­сти.

При упорядочении статистических величин в совокупности образу­ются группировочные интервалы. Тогда под обозначением ∆Х пони­мается размах интервала, а среднее интервальное значение обозначается Х_И.

Методику расчета средних величин и коэффициентов вариации рас­смотрим на примере группы студентов или слушателей из 21 чел. (N =21), каждый из которых имеет возраст X = 28, 36, 30, 22, 22, 40, 29, 27, 21, 23, 35, 30, 32, 33, 29, 37, 29, 39, 23, 22, 22 лет. Требуется определить средний возраст и установить его типичность или нетипичность с помощью линейного и квадратического коэффициентов вариации.

Поскольку данные не упорядочены, то средний возраст определяем по формуле (1.13) как простую среднюю арифметическую величину

= (28+36+30+…+23+22+22)/21 = 29 лет.

Для применения формулы средней арифметической взвешенной выполним первичную (дискретную) группировку данных, расположив их в порядке увеличения возраста и определяя повторяемость, встречаемость или частоту одинакового возраста, как показано в табл. 1.1.

Таблица 1.1

Первичная или дискретная группировка данных

Xi	21	22	23	27	28	29	30	32	33	35	36	37	39	40
fi	1	4	2	1	1	3	2	1	1	1	1	1	1	1	21

Тогда по формуле (1.14) средний возраст будет равен

= (21*1+22*4+23*2+…+37*1+39*1+40*1)/21 = 29 (лет).

Хотя результат и оказался одинаковым, но первичная группировка дает более четкое представление о структуре статистической совокуп­ности. В данном примере это возрастная структура группы студентов. К тому же, она позволяет перейти к определению линейного коэффици­ента вариации.

Так, по формуле (1.23) среднее линейное отклонение взвешенное равно

Л = 4,857 лет

а линейный коэффициент вариации по формуле (1.28) равняется

= 4,857/29 = 0,168

Вывод: средний возраст 29 лет является типичным для рассмотрен­ной группы студентов, т.к. расчетный коэффициент вариации оказался меньше его критериального значения (0,168 0,333).

Дополнительно определяется коэффициент осцилляции, для чего предварительно по формуле (1.31) находим размах вариации

R = 40-21 = 19 (лет).

Значит, по формуле (1.30) коэффициент осцилляции равняется

Кос = 19/29 = 0,655.

Для нахождения квадратического коэффициента вариации выполним вторичную (интервальную) группировку данных, используя формулу Стерджесса для определения оптимального количества интервалов п. Эта формула имеет вид

n = 1 +3,322 lg N, (1.33)

позволяя затем находить необходимый размах интервала как отношение

X_и = R / n. (1.34)

Подставляя данные примера в эти формулы, находим количество ин­тервалов n =1+ 3,322 lg 21 = 1+3,322*1,322 = 5,4. Так как количество интервалов не может быть дробным, то его нужно округлить до ближайшего целого числа (по правилам округления). То есть нужно принять 5 интервалов.

По формуле (1.32) размах интервала будет равен 19/5 = 3,8, то есть 3,8 года. Интервальная группировка данных приведена в первом столбце табл. 1.2, которая содержит также алгоритм и промежуточные расчеты.

Таблица 1.2 Промежуточные расчеты по интервальной группировке данных

Xi , лет	fi	ХИ	XИfi	ХИ-	(ХИ- )^2	(ХИ- )^2fi
до 24,8	7	22,9	160,3	-6,333	40,111	280,7778
24,8-28,6	2	26,7	53,4	-2,533	6,418	12,83556
28,6-32,4	6	30,5	183	1,267	1,604	9,626667
32,4-36,2	3	34,3	102,9	5,067	25,671	77,01333
36,2-40	3	38,1	114,3	8,867	78,618	235,8533
Итого	21	—	613,9	—	—	616,1067

В табл. 1.2 пер­вый и последний интервалы открытые, не имея нижней или верхней границы диапазона, а промежуточные интервалы закрытые, имея обе границы. Нахождение середин закрытых интервалов затруднений не вызывает, а с открытыми интервалами поступают следующим образом: к открытому интервалу применяют размах соседнего (смежного), но так как размах всех интервалов в нашем примере одинаков и равен 3,8 года, то и здесь затруднений не должно быть.

У первого интервала отсутствует нижняя граница и находят ее путем вычитания размаха смежного интервала из имеющейся верхней грани­цы, получая тем самым закрытый интервал, середина которого опреде­ляется легко. В данном примере имеем 24,8–3,8 = 21 год, значит, середина этого интервала будет равна (21+24,8)/2 = 22,9 года.

У последнего интервала отсутствует верхняя граница и находят ее путем прибавления размаха смежного интервала к имеющейся нижней границе, получая тем самым также закрытый интервал. В данном при­мере имеем 36,2+3,8 = 40 (лет), значит, середина интервала 36,2-40 будет 38,1 лет.

По итогам табл. 1.2 определяются такие характеристики, как средний возраст по формуле (1.14)

= 613,9/21 = 29,2333 (лет).

Как видим, результат несколько отличается от предыдущего, что вы­звано неизбежным округлением расчетного количества интервалов. Чем больше количество интервалов и меньше их размах, тем меньше будет разница в результатах.

Затем по формуле (1.25) определяется взвешенная дисперсия откло­нений

Д = 616,1067/21=29,3384 лет².

Далее по формуле (1.26) находится среднее квадратическое отклоне­ние

= = 5,4165 лет.

И, наконец, по формуле (1.29) рассчитывается квадратический ко­эффициент вариации

= 5,4165 /29,2333 = 0,185.

По значению этого коэффициента делается вывод о типичности среднего возраста 29,23 лет для рассмотренной группы студентов, т.к. расчетное значение коэффициента вариации не превышает критериаль­ного (0,185 < 0,333).