
- •14. Понятие преобразования плоскости. Перемещения плоскости, их виды.
- •15. Преобразование подобия. Гомотетия.
- •16. Теоретико-множественный смысл колич-го натур-го числа и нуля. Отношения равенства и неравенства на мн-ве целых неотриц-х чисел.
- •17. Теоретико-множественный смысл суммы 2х ц.Н.Ч. Законы сложения.
- •2)Ассоциативный
- •18. Теоретико- множественный смысл разности целых неориц-х чисел. Определение разности через сумму. Условие сущ-ия разности на мн-ве ц.Н.Ч.
- •19.Теоретико-множественный смысл произведения целых неотриц-х чисел. Определение произв-я через сумму. Законы умножения.
- •2) Ассоциативный
- •4)Дистрибутивный относ-но «-»
- •20.Теоретико- множественный смысл частного целого неотриц-го числа и натур-го. Опред-ие частного через произведение. Условие сущ-ия частного на мн-ве натур-х чисел.
- •21. Отношение делимости на множестве натуральных чисел, его св-ва. Теоремы о делимости суммы, разности и произведения целых неотриц. Чисел.
- •22. Понятие о системе счисления. Запись чисел в десятичной си-ме счисления. Операции над целыми неотриц-ми числами в десятичной системе счисления.
- •24. Положительные действительные числа и операции над ними. Законы сложения и умножения на мн-ве положительных действительных чисел.
- •25. Понятие величины и ее измерения.
1.Понятие мн-ва. Отнош-я м/у мн-ми. Операции пересеч и объед мн-в, законы этих операций. Мн-во-некоторая совок-ть объектов. Объекты из кот состоят мн-ва – наз-ся его элементами. Мн-во обозначают большими буквами лат алфавита: А,B,C,D, а его элементы – малыми: a,b,c,d. Мн-во, кот не содержит ни 1-го элемента наз пустым. Мн-ва быв-т конеч-е и бескон-е. Отношения мн-ва: 1) пересеч-я (если элементы принадлежат к 1-му и 2-му мн-ву одновр-но); 2) включения (подмн-во, если каждый элемент 1-го мн-ва явл элементом 2-го мн-ва); 3) равенства (если 2 мн-ва состоят из одних и тех же элементов). Мн-во наз-ся универсальным, если все мн-ва явл его подмнож-ми. Пересеч-м мн-в А и В наз-ся мн-во, кот состоит из тех и только тех элементов, кот одноврем-но принадлежат и мн-ву А и мн-ву В. Объединением мн-в А и В наз-ся мн-во, кот состоит из тех и только тех элементов, кот входят хотя бы в одно из мн-в А или В. Законы пересеч-я мн-в: 1) коммутативный (перемест-й) 2) ассоциативный (сочитательный) Сочитательный закон позволяет находить пересеч-я и оъед-я 3-х и более мн-в, а также записывать выражения без скобок. 3) дистрибутивный (распределительный) (пересеч-е относительно объедин-я) 4) объединения: 1) 2) 3) 4)
2. Вычитание мн-в, дополнение к подмн-ву,декартово произаед-е 2-х мн-в и их св-ва. Разностью мн-в a и b наз-ся мн-во, состоящее из всех тех и только тех мн-в а, кот не принадлежат мн-ву b. Разность мн-в обозн-ся \. Если мн-во В явл подмн-м А, то разность мн-в А и В наз-ся дополнением В во мн-ве А и обознач-ся дополнение во мн-ве В подмн-во А. . Дополнение к подмн-ву В в универсальном мн-ве обознач-ся В'. Декартово произв-е 2х мн-в. Каждый элемент входит во мн-во только 1 раз,при этом порядок записи элементов м/б разным. Однако,часто приходится учитывать и порядок в кот наход-ся данные элементы (напр, 742 и 427-мн-во цифр одинаково, а числа разные). Вводится новое понятие кортеж-конечная упорядоченная последоват-ть (кот допускает повторение) элементов некоторого мн-ва. Элементы кортежа закл-ся в круглые или ломаные скобки. Кол-во элементов в кортеже назыв-ся его длиной, а сами элементы компонентами или координ кортежа. 2 кортежа назыв-ся равными, если имеют одинак-ю длину и их соотв-е компоненты равны. Декартово призв-е и их св-ва. Декарт-м призвед-м 2х мн-в а и b наз-ся мн-во пар,у кот первая компонента принадлежит мн-ву а,а вторая мн-ву b. Св-ва: 1) декатрово произвед-е 2 мн-в на коммутативно (нельзя переставлять мн-ва а и b) 2) дек-во произв-е не ассоциативно 3) дистрибут-й з-н относительно операций пересечения, объединения, разности мн-в как слева, так и справа выполняются.
3.
Понятие комбинаторной задачи. Правила
+ и *.
Перестановки,
размещения без повторений и с повторениями,
сочетание без повторений. Раздел
матем-ки, кот рассматр-т задачи,связан-е
с комбиниров-мэлементов мн-ва наз-т
комбинаторикой. В основе всей теории
лежат 2 осн правила: прав-ло суммы и
произвед-я. Правило + позволяет найти
число элементов в объединении 2х или
неск-х мн-в, кот не пересек-ся. Комбинат-е
правило + формулировка: если выбор одного
объекта м осущ-ть Р1-различными
способами,Р2-различными способами,
отличных от предыдущ-го и т д, то выбор
какого-нибудь одного объкта из все
данных объектов м осущ-ть Р1+Р2+…спос-ми.
Правило нахожд-я элементов декартово*
в комбинаторике наз-ся правилом *. Для
2х мн-в оно формируется: если элемент х
м выбрать из 1-го мн-ва n-способами,
а элемент у из 2-го мн-ва m-способами,
то упорядоченную пару (х;у) м выбрать
m*n
способами. Обобщенное правило *. Если
1-й элемент м выбрать m1
сп-ми, после этого 2-й элемент м выбрать
m2
сп-ми и т д.n-й
элемент м выбрать mn
спос-ми, то упорядоченну n-ку
элементов м выбрать m1*m2…
способами. Мн-во наз упорядоч-м,если его
элементы расположены в соотв-м порядке.
В уроряд-м мн-ве все элементы
различны.различ-е кпорядоч-я 1-го и того
же мн-ва состоят из одних и тех же
элементов и отлч-ся лишь порядком
элементов. Перестан-й
без повтор-й
наз всякое упорядоченное мн-во. Теорема:
число СП-в кпорядочения n-элем-го
мн-ва опред-ся по формуле Рn=n!,
где Рn-это
число перестановок из n-элементов
n!-
n-факториал,
n!-произвед-е
все N
от 1 до n
(1, 2, 3… n)
(напр. 3! – 1*2*3=6.). Размещение
без повторений
наз-ся каждое упорядоч-е к-элементное
подмн-во данного n-элем-го
мн-ва. Теорема:число элементов размещений
из n-элем
по к-элем опред-ся по формуле. A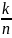 =
=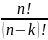 .
Сочетанием
без повторений
наз каждое к-ое подмн-во данного n-элем-го
мн-ва обознач-ся Сn.
Теорема: кол-во сочетаний без повторений
из n-элем
по к вычисляется по формуле С
.
Сочетанием
без повторений
наз каждое к-ое подмн-во данного n-элем-го
мн-ва обознач-ся Сn.
Теорема: кол-во сочетаний без повторений
из n-элем
по к вычисляется по формуле С .
Кол-во упорядоченных к-элем-х подмн-вданного
n-элем-го
мн-ва выч-ся по формуле A
=
.
Кол-во упорядоченных к-элем-х подмн-вданного
n-элем-го
мн-ва выч-ся по формуле A
=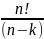 . Тогда кол-во неупоряд-х подмн-в будет
в к! раз меньше, чем кол-во упорядоченных
т к из каждого неупоряд-го подмн-ва кот
содержит к-элементов м составить
к-факториал упорядоч-х подмн-в. Т. о.
С
=
. Тогда кол-во неупоряд-х подмн-в будет
в к! раз меньше, чем кол-во упорядоченных
т к из каждого неупоряд-го подмн-ва кот
содержит к-элементов м составить
к-факториал упорядоч-х подмн-в. Т. о.
С
=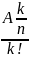 =
=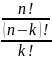 =
= .
.
Размещения
с повторениями
наз кортеж длины к составленный из
k-элементного
мн-ва (k
м/б
 n).
Кол-во размещ-й из n-элем
по к обозн-ся
n).
Кол-во размещ-й из n-элем
по к обозн-ся
 .
Теорема: кол-во размещ-й с повторен-ми
из n-элем
выч-ся по формуле
=nk.
Перестановки с повтор-ми наз любой
кортеж длины n
n-элем-го
мн-ва. Обозн-ся
.
Теорема: кол-во размещ-й с повторен-ми
из n-элем
выч-ся по формуле
=nk.
Перестановки с повтор-ми наз любой
кортеж длины n
n-элем-го
мн-ва. Обозн-ся
 n.
Теорема: кол-во различных перестановок
с повтор-ми n-элем
мн-ва, в кот один из элементов повтор-ся
n1
раз, 2-й элемент n2
раз и т д, к-й элемент повтор nk
раз вычиисл по формуле
n=
n.
Теорема: кол-во различных перестановок
с повтор-ми n-элем
мн-ва, в кот один из элементов повтор-ся
n1
раз, 2-й элемент n2
раз и т д, к-й элемент повтор nk
раз вычиисл по формуле
n=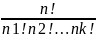 .
.
4. Понятие высказывания. Конъюнкция и дизъюнкция высказываний, законы этих операций. Высказывание-это повествоват-е предложение относит-но которого м утверждать истинно оно или ложно. Конъюнкцией выск-й А и В наз составное высказ-е А и В истинное тогда и т т, к оба высказ-я А и В истинны и ложно если хотя бы 1-но из высказ-й ложно. Обозн-ся ˄ . Можно находить конъюнкцию 3 или несколько высказываний. Она будет истина т и т т, если одновременно истинны все высказывания, кот входят в нее. Дизъюнкцией высказ-й А и В наз высказ-е А или В, кот явл истинным, если хотя бы одно из высказ-й и ложным, если оба высказывания ложны обозн-ся А ˅ В. Законы: 1) коммутативный (переместительный) з-н А˄В=В˄А; А˅В=В˅А; 2) ассоциативный (сочитательный) А˄(В˄С)=(А˄В)˄С; А˅(В˅С)=(А˅В)˅С; 3) а) дистрибутивный з-н коньюнкции относит-но дизьюнкции А˄(В˅С)=(А˄В)˅(А˄С); б) дистрибутивный з-н дизьюнкции относит-но коньюнкции А˅(В˄С)=(А˅В)˄(А˅С); 4) А˄А=А; А˅А=А; А˄И=А; А˅И=А; А˄Л=А; А˅Л=А.
5.
Отрицание, импликация и эквиваленция
высказываний, законы этих операций.
Отрицанием
высказыв-я А наз-ся высказ-е «не А», кот
явл истенным, если А-ложно и ложным, если
А-истенно, обозн-ся
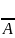 (не правда, что А). Импликацией наз
составное высказыв-е, «если А,то В».
Ложно т и т т, если А-истинно, а В-ложно.
В остальных случаях импликация истинна.
Обозн
(не правда, что А). Импликацией наз
составное высказыв-е, «если А,то В».
Ложно т и т т, если А-истинно, а В-ложно.
В остальных случаях импликация истинна.
Обозн
 .
Виды: 1) А
В-прямая;
2) В
А-обратная
(меняем местами условие и заключение);
3) Из
.
Виды: 1) А
В-прямая;
2) В
А-обратная
(меняем местами условие и заключение);
3) Из
 -
противопол-я (строим отрицание условия
и заключения в прямой теореме); 4) Если
-
противопол-я (строим отрицание условия
и заключения в прямой теореме); 4) Если
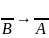 -
противопол-но обратной или обратная
противоположной. Эквиваленцией
наз составное высказыв-е А т и т т , когда
В, оно истинно, если оба высказывания
истинны или оба ложны и ложно, если
высказ-е А и В имеют разные значения
истинности. Закон для отрицания
высказывания: 1) закон двоиного отрицания
(А=
-
противопол-но обратной или обратная
противоположной. Эквиваленцией
наз составное высказыв-е А т и т т , когда
В, оно истинно, если оба высказывания
истинны или оба ложны и ложно, если
высказ-е А и В имеют разные значения
истинности. Закон для отрицания
высказывания: 1) закон двоиного отрицания
(А= );
2) з-н противоречия А
);
2) з-н противоречия А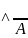 =Л;
3) з-н исключения третьего А˅
=И;
4) з-н де Моргана а)
=Л;
3) з-н исключения третьего А˅
=И;
4) з-н де Моргана а)
 =
˅
=
˅ ;
б) А˅В=
˄
.
Законы для импликации: 1) з-н, кот связыв-т
импликацию с отрицат и дизьюнкцией
высказываний. А
;
б) А˅В=
˄
.
Законы для импликации: 1) з-н, кот связыв-т
импликацию с отрицат и дизьюнкцией
высказываний. А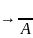 ˅В;
2) з-н контрапозиции А
В=
;
3) з-н эквиваленции связывает коньюнкцию
импликации А
˅В;
2) з-н контрапозиции А
В=
;
3) з-н эквиваленции связывает коньюнкцию
импликации А В=(А
В)˄(В
А).
В=(А
В)˄(В
А).
6.
Понятие предиката.
Конъюнкция,дизъюнкция,отрицание,импликация
и эквиваленция предикатов, их мн-ва
истинности.
Предикат-это предложение с одной или
несколькими перемен-ми и кот при конкрет-х
значениях перемен-х превращ-ся в
высказыв-е. по числу переменных, входящих
в предикат выделяют: одноместные,
двуместные и т д. преликаты. С каждым
предикатом связаны 2 мн-ва: 1-мн-во
определения предиката (обознач-ся х-это
мн-во тех значений переменной, при кот
предикат обращ в высказывание); 2-мн-во
истинности предиката-это мн-во тех знач
переменной из области определения при
кот предикат превращается в истинное
высказывание Т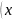 .
обноместные преликаты обозн А(х), х
.
обноместные преликаты обозн А(х), х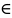 Х(читается- на мн-ве А задан предикат)
(напр. А(х): число х-простое). 2 предиката
А(х) и В(х) заданные на одном и том же
мн-ве х наз-ся равносильным (эквивалентным),
если они имеют одно и тоже мн-во истинности
и запис-ся А(х)
Х(читается- на мн-ве А задан предикат)
(напр. А(х): число х-простое). 2 предиката
А(х) и В(х) заданные на одном и том же
мн-ве х наз-ся равносильным (эквивалентным),
если они имеют одно и тоже мн-во истинности
и запис-ся А(х) В(х).(напр
А(х):х+2=4, х
N;
В(х):
В(х).(напр
А(х):х+2=4, х
N;
В(х):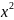 -4=0,х
N.
-4=0,х
N.
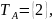
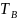 =
=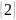 ,
,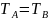 А(х)
В(х)).
Предикаты: элементные, составные.
Состав-е образовыв-ся из элементарных
при помощи логически связанных
высказываний. Отрицанием
предиката А(х) наз-ся предикат не
А(х),записанный на том же мн-ве х. он
истинен при тех значениях, при кот
предикат А(х) ложен. Конъюнкцией А(х) и
В(х) наз-ся составной предикат А(х) и В(х)
заданный на том же мн-ве х. Он истинен
когда одновременно истинны оба предиката
А(х) и В(х). Мн-во истинности конъюнкции
предиката А(х) и В(х) явл перечисление
мн-в истинности предикатов. Дизъюнкцией
наз-ся
составной предикат А(х) и В(х) задан на
том же мн-ве х. А(х)
А(х)
В(х)).
Предикаты: элементные, составные.
Состав-е образовыв-ся из элементарных
при помощи логически связанных
высказываний. Отрицанием
предиката А(х) наз-ся предикат не
А(х),записанный на том же мн-ве х. он
истинен при тех значениях, при кот
предикат А(х) ложен. Конъюнкцией А(х) и
В(х) наз-ся составной предикат А(х) и В(х)
заданный на том же мн-ве х. Он истинен
когда одновременно истинны оба предиката
А(х) и В(х). Мн-во истинности конъюнкции
предиката А(х) и В(х) явл перечисление
мн-в истинности предикатов. Дизъюнкцией
наз-ся
составной предикат А(х) и В(х) задан на
том же мн-ве х. А(х)
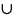 В(х) / А(х) или В(х), х
Х.
он истинен тогда, когда хотя бы 1-н из
предикатов истинен. Импликацией
наз-ся
составной предикат А(х)
В(х),
ели А(х), то В(х) задан на том же мн-ве х.
Он ложен когда А(х)-И, а В(х)-Л, при остальных
И. Эквиваленцией наз-ся составной
предикат А(х)
В(х),
х
Х.
Истинно только когда оба И или оба Л,
при остальных ложно.
В(х) / А(х) или В(х), х
Х.
он истинен тогда, когда хотя бы 1-н из
предикатов истинен. Импликацией
наз-ся
составной предикат А(х)
В(х),
ели А(х), то В(х) задан на том же мн-ве х.
Он ложен когда А(х)-И, а В(х)-Л, при остальных
И. Эквиваленцией наз-ся составной
предикат А(х)
В(х),
х
Х.
Истинно только когда оба И или оба Л,
при остальных ложно.
7.
Матем-е понятия. Объем и содерж-е понятия.
Способы определения понятий. Требования
к определению понятий.
Объем понятия-это мн-во объектов,
обозначаемых одним и тем же термином.
Если объем понятия А явл частью объема
понятия В ( )
) )
понятие А наз-т видовым по отношению к
понятию В, а понятие В родовым по отношению
к В (напр. Понятие ромб явл видовым
понят-м параллелограмма, а понятие
параллелограмм это родовое понятие для
ромба). Содерж-е понятия-это совокупность
св-в данного понятия. М/у объемом и
содерж-м понятия сущ-т связь:чем больше
объем понятия, тем меньше его содержание.
Чем больше содержание тем меньше его
объем. Понятие-логич-я операция, кот
раскрывает содержание понятия. Осн
сп-бы определения понятий:
1) определение понятия ч/з род и видовое
отличие. При этом СП-бе указыв-ся более
общее родовое понятие, а затем указыв-ся
видовое отличие, то св-во кот выделяет
данный вид издр видов данного рода.
Определение
понятия = родовое понятие + видовое
понятие (напр.
Квадрат=это прямоугольник, у кот все
стороны равны); 2) генетические. Указывает
на происхождение понятий(сфера,
окружность…); 3) аксиоматический
сп-б-определение понятия ч/з с-му аксиом;
4) индуктивный сп-б. Это сп-б получения
все элементов понятия арифм и геометр
прогрессии; 5) контекстуальные определения.
Опред-е понятия ч/з текст; 6) Остенсивные
определения- определение понятия ч/з
демонстрацию. Осн требования к опред
понятий: 1) определяемое и определяющее
понятие д/б соразмерным (их объемы д
совпадать); 2) в определении понятия д/б
указаны св-ва, кот позволяют выделить
данный объект среди мн-ва др объектов;
3) отсутствие в отрицании избыточности;
4) запрещается порочный круг. Нельзя
определить понятие ч/з само себя или
понятие определить ч/з другое ч/з первое;
5) определяемый объект д существовать.
)
понятие А наз-т видовым по отношению к
понятию В, а понятие В родовым по отношению
к В (напр. Понятие ромб явл видовым
понят-м параллелограмма, а понятие
параллелограмм это родовое понятие для
ромба). Содерж-е понятия-это совокупность
св-в данного понятия. М/у объемом и
содерж-м понятия сущ-т связь:чем больше
объем понятия, тем меньше его содержание.
Чем больше содержание тем меньше его
объем. Понятие-логич-я операция, кот
раскрывает содержание понятия. Осн
сп-бы определения понятий:
1) определение понятия ч/з род и видовое
отличие. При этом СП-бе указыв-ся более
общее родовое понятие, а затем указыв-ся
видовое отличие, то св-во кот выделяет
данный вид издр видов данного рода.
Определение
понятия = родовое понятие + видовое
понятие (напр.
Квадрат=это прямоугольник, у кот все
стороны равны); 2) генетические. Указывает
на происхождение понятий(сфера,
окружность…); 3) аксиоматический
сп-б-определение понятия ч/з с-му аксиом;
4) индуктивный сп-б. Это сп-б получения
все элементов понятия арифм и геометр
прогрессии; 5) контекстуальные определения.
Опред-е понятия ч/з текст; 6) Остенсивные
определения- определение понятия ч/з
демонстрацию. Осн требования к опред
понятий: 1) определяемое и определяющее
понятие д/б соразмерным (их объемы д
совпадать); 2) в определении понятия д/б
указаны св-ва, кот позволяют выделить
данный объект среди мн-ва др объектов;
3) отсутствие в отрицании избыточности;
4) запрещается порочный круг. Нельзя
определить понятие ч/з само себя или
понятие определить ч/з другое ч/з первое;
5) определяемый объект д существовать.
8.
Понятие об уравнении с 1-й переменной и
мн-ве его решений. Равноильные уравнения.
Теоремы о равносильных уравнениях.
Пусть
f(х)
и g(х)-выражения
с 1й переменной, заданные на мн-ве х
предикатами вида f(х)=g(х),
заданный на мн-ве х наз-ся уравнением с
1й переменной. (напр. 2х+3=3х-8,х
R).корнем
уравнения наз-ся значение переменной
из области определения при кот ур-ие
преврашается в верное числовое равенство.
Решить уравнение, значит найти мн-во
корней этого уравнения. Уравление
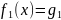 (х)
явл следствием уравн-я
(х)
явл следствием уравн-я
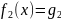 (х),
если мн-во корней 2-го уравн-я явл подмн-м
мн-ва корней 1-го уравн-я или уравн-е
(х)
явл следствием уравн-я
(х),
если каждый корень 2-го уравн-я явл корнем
уравн-я 1-го.
(х),
если мн-во корней 2-го уравн-я явл подмн-м
мн-ва корней 1-го уравн-я или уравн-е
(х)
явл следствием уравн-я
(х),
если каждый корень 2-го уравн-я явл корнем
уравн-я 1-го.
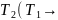 (2)
(1).
Теорема
1
о равенстве уравн-й и следствия из них.
Если к каждой части уравн-я n
f(х)=g(х)
заданных на мн-ве х, прибавить одно и
тоже выражение с переменной, n(x),
заданное на том же мн-ве х, то получим
уравн-е f(x)+h(x)=g(x)+h(х)
равносильно данному. Следствие из
теорем: 1) к каждой части уравн-я м
прибавить одно и тоже число; 2) слагаемы
в уравн-и м переносить из одной части
уравн-я в другую с противоположным
знаком. Теорема
2.
Если каждую часть уравн-я f(х)=g(х)
заданного на мн-ве х умножить на одно и
тоже выражение h(x)
заданного на томже мн-ве х и не равно 0,
то получим уравнение f(x)*h(x)=g(x)*h(х)
равносильно первому. Следствие: обе
части уравн-я м умножить или разделить
на одно и тоже число, отличное от нуля.
(2)
(1).
Теорема
1
о равенстве уравн-й и следствия из них.
Если к каждой части уравн-я n
f(х)=g(х)
заданных на мн-ве х, прибавить одно и
тоже выражение с переменной, n(x),
заданное на том же мн-ве х, то получим
уравн-е f(x)+h(x)=g(x)+h(х)
равносильно данному. Следствие из
теорем: 1) к каждой части уравн-я м
прибавить одно и тоже число; 2) слагаемы
в уравн-и м переносить из одной части
уравн-я в другую с противоположным
знаком. Теорема
2.
Если каждую часть уравн-я f(х)=g(х)
заданного на мн-ве х умножить на одно и
тоже выражение h(x)
заданного на томже мн-ве х и не равно 0,
то получим уравнение f(x)*h(x)=g(x)*h(х)
равносильно первому. Следствие: обе
части уравн-я м умножить или разделить
на одно и тоже число, отличное от нуля.
9. Понятие о нер-ве с 1й переменной и мн-ве его решений. Равносильные нер-ва. Теоремы о равносильных нер-вах. (Напр 1-х 3х-2,х Х – это предложение явл предикатом, такие предикаты наз-т нер-ми с 1й переменной). Предикатом вида f(х) g(х) или f(х) g(х) заданный на мн-ве х наз-ся нерав-м с 1й переменной. Мн-вом решений нер-ва f(х) g(х) заданным на мн-ве х наз мн-во истинности этого предиката, а каждый элемент этого мн-ва наз-ся решением нер-ва. Значение перемен-й х=а, при кот нер-во превращается в истинное числовое нер-во назыв его решением. Если кажд решение 1го нер-ва явл решением 2го нер-ва, то 2-е нер-во наз следствием 1го. 2 нер-ва наз равносильными, если их мн-во решений совпадают. Теорема 1 о равносильности нер-в. Если в каждой части нер-ва f(х) g(х) заданного на мн-ве прибавить одно и тоже выражение с переменной h(x), x Х, то получим нер-во f(x)+h(x)=g(x)+h(х) равносильное исходному. Следствие из теоремы: 1) если к каждой части нер-ва прибавить одно и тоже число, то получим нер-во равносильное данному; 2) члены нер-ва м переносить из 1й части в другую с противопол-м знаком. Теорема 2 Если обе части нер-ва f(х) g(х) заданного на мн-ве х умножить на одно и тоже выражение с переменной h(x) заданное на томже мн-ве х и положит-е на нем, то получим нер-во f(x)*h(x) g(x)*h(х) равносильное исходному. Следствие из теоремы: если обе части нер-ва умножить на одно и тоже положит-е действительное число, то получим нер-во равносильное данному. Теорема 3 Если обе части нер-ва f(х) g(х) заданного на мн-ве х умножить на одно и тоже выраж-е с переменной h(х) заданного на том же мн-ве х и отрицательное на нем, то получим нер-во f(x)*h(x) g(x)*h(х) равносильно данному. Следствие: если обе части нер-ва умножить на одно и тоже отрицат-е действ-е число и при этом знак нер-ва поменять на противопол-й, получим нер-во равносильное данному.
10.
Бинарные отношения м/у элементами 2х
мн-в, сп-бы из задания. Виды отношений
м/у элементами 2х мн-в. Бинарным
соответствием м/у элем-ми мн-в х и у наз
любое ( декартово произ-е этих мн-в.
Обознач-ся больш буквами лат алфавита,
обычно не первые а кот стоят в конце
алфавита (R,S,T..).
для задания соответствия м/у элементами
мн-в х и у надо указать ( дек-во произв-е
х и у – это подмн-во обознач-ся Г.
Соответствие – упорядоченная тройка
мн-в, где (Х, У, Г), где Г(х*у. если а и b
элементы мн-в Х; У, т. е. а
х,
b
у
и элемент а наход-ся в соответствии R
с элементом b,
то это запис-ся- aRb,
(a,b)
R(элемент
а наход-ся в соотв-и Rс
элементом b).
Мн-во х наз-ся мн-ом отправления
соответствия R,
а мн-во у мн-ом прибытия соответст-я R.
Мн-во 1х компонентов пар, кот
соответ-ю R
наз областью опред-ия соответствия, а
мн-во др компанентов пар наз мн-ом
значений соответствия. Т. к. соотв-е
это мн-во, то его м задать теми же сп-ми,
что и любое мн-во . 1)
Если мн-во х и у конечные, то соотв-е м
задать перечислением. Форма записи пар
м/б различной: а) в виде мн-ва; б) таблицы;
в) графа; в виде рисунка, в кот мн-во х и
у показывают авалами. Элементы мн-в х и
у обозн-т авалами, элементы обозн-т
точками, а соответствие стрелками. 2)
указание характеристич-го св-ва всех
пар, кот
соответствию R.
3)
если мн-во х и у числовые, то соответствие
м/у элементами этих мн-в м задать при
помоши графика на координатной пл-ти.
Соответствие R
наз полным, если график Г совпадает с
декартовым * мн-в (х;у) (Г=х;у). Если график
соответствия R
есть пустое мн-во, то соответствие R
наз пустым. Соответствием, обратным
соответствию R
м/у элементами мн-в (х;у) наз соответствие
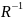 м/у мн-ми у и х такое, что У
Х тогда и т т , к х R
у. для того, чтобы получить обратное
соответв-е необходимо поменять местами
компаненты пар. Для того, чтобы построить
граф обратного соответствия достаточно
поменять направление всех стрелок в
графе в соответст-и с R.
Если мн-во х и у числовые, то графики
соответст-я R
м/у мн-ми у и х такое, что У
Х тогда и т т , к х R
у. для того, чтобы получить обратное
соответв-е необходимо поменять местами
компаненты пар. Для того, чтобы построить
граф обратного соответствия достаточно
поменять направление всех стрелок в
графе в соответст-и с R.
Если мн-во х и у числовые, то графики
соответст-я R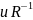 симметричны относительно биссектрисы
1го и 3го координат-х углов. Соответст-е,
график кот явл дополнение-м графика
соответст-я R
до декарт-во * мн-в х и у наз противопол-м
для соответст-я R
и обознач-ся
симметричны относительно биссектрисы
1го и 3го координат-х углов. Соответст-е,
график кот явл дополнение-м графика
соответст-я R
до декарт-во * мн-в х и у наз противопол-м
для соответст-я R
и обознач-ся
 . соответст-я
. соответст-я
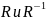 наз взаимнопротивопол-м. Графики
взаимнопротивопол-м соответствий не
пересекаются, а их объединения есть
мн-ва.
наз взаимнопротивопол-м. Графики
взаимнопротивопол-м соответствий не
пересекаются, а их объединения есть
мн-ва.
11.
Бинарные отнош-я м/у элементами 1го
мн-ва. Св-ва отношений. Отношения
эквиваленции и порядка.
Если мн-во х и у совпадают, то говорят
не об соответствии, а об отношениях м/у
элементами мн-ва х. Бинарным отношением
м/у мн-ми наз всякое подмн-го Г декартово
* мн-в Х*Х. Т. о. бинарное отношение R,
заданное на мн-ве х-это пара мн-в (Х;Г),
где х-это мн-во задания отнош-я R,
а Г-график отношен-я R
и график (Г(Х*Х). Т.к. отношение – есть
частный случай соответствия, то все
сказанное выше соответствия остается
истинный и для отношений. Св-ва отношений:
1) отношение R
на мн-ве х наз рефлексивным, если любой
элемент из мн-ва х находится в отношении
R
с самим собой; 2) отношение R
на мн-ве х наз антирефлексивным, если
ни один элемент мн-ва х не наход-ся в
отношении R
с самим собой; 3) отношение R
на мн-ве х наз симметрич-м, если для любых
2 элементов х и у из мн-ва х из того, что
элемент х находится в отношении R
с элементом у следует, что и элемент у
находится в отношении R
с элементом х; 4) отношения х на мн-ве R
наз антисимметричным, если для разным
элементов х и у из мн-ве х из того, что
элемент х наход-ся в отношении R
с элементом у, следует, что элемент у
не наход-ся в отношении R
с элементом х; 5) отношение R
на мн-ве х наз транзитивным, если для
любых элементов х;у;z
из мн-ва х, из того , что элемент х наход-ся
в отношении R
с элементом у, а элемент у нах-ся в
отношении R
с элементом Z,
следует что элемент х наход в отнош-и R
с элементом Z.
Отношением эквиваленьности – если оно
рефлексивное, симметричное, транзитивное.
Примером отнош-я эквивалентности явл
отношение параллельности на мн-ве прямых
пл-ти: 1) любая прямая параллельна самой
себе, данное отношение рефлексивно; 2)
если а b,
то b‖а,
отнош-е симметрично на мн-ве прямых; 3)
если а‖b,
b‖c,
a‖c,
отношение транзитивно. Каждое отношение
эквивалентности разбивает мн-во, кот
оно разбивает на классы. Отношение R
на мн-ве х наз отношением порядка, если
оно на этом мн-ве облад-т свойствами
антисимметричности и транзит-ти
Св-ва: антирефлексивно,
антисимметр-но, транзитивно. Различают
порядок строгий и нестрогий. R
на мн-ве х наз отношением строгого
порядка, если оно антирефл, антисимметр,
транзит. Отнош-е R
наз отнош-е нестрогого порядка, если
отнош-е Rрефлек,
антисимм, транзит. Порядок бывает
линейным и частичным. Отнош порядка R
(строгого или нестрогого) на мн-ве х наз
отнош-м линейного порядка, если оносвязное,
т е любые 2 элемента из мн-ва х связаны
этим отношением. Если отнош-е R
таким св-вом не обладает, то его наз
частичным
b,
то b‖а,
отнош-е симметрично на мн-ве прямых; 3)
если а‖b,
b‖c,
a‖c,
отношение транзитивно. Каждое отношение
эквивалентности разбивает мн-во, кот
оно разбивает на классы. Отношение R
на мн-ве х наз отношением порядка, если
оно на этом мн-ве облад-т свойствами
антисимметричности и транзит-ти
Св-ва: антирефлексивно,
антисимметр-но, транзитивно. Различают
порядок строгий и нестрогий. R
на мн-ве х наз отношением строгого
порядка, если оно антирефл, антисимметр,
транзит. Отнош-е R
наз отнош-е нестрогого порядка, если
отнош-е Rрефлек,
антисимм, транзит. Порядок бывает
линейным и частичным. Отнош порядка R
(строгого или нестрогого) на мн-ве х наз
отнош-м линейного порядка, если оносвязное,
т е любые 2 элемента из мн-ва х связаны
этим отношением. Если отнош-е R
таким св-вом не обладает, то его наз
частичным
12.
Фунциональные отношения. Числовые
функции. Прямая и обратная пропорциональности,
их св-ва и графики.
Прямая прапорц-ть – наз ф-ция, кот м/б
задана при помощи формулы вида y=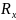 ,
где х- независимая переменная, а
R-действительное
число. Для того, чтобы найти коэффициент
пропорциональности R,
достаточно знать пару соотв-х значений(х;у),
за исключ пары (0;0), т к R=
,
где х- независимая переменная, а
R-действительное
число. Для того, чтобы найти коэффициент
пропорциональности R,
достаточно знать пару соотв-х значений(х;у),
за исключ пары (0;0), т к R= .
Св-ва: 1) область определ (Д). Д(у)= R;
2) Мн-во значений (Е). Е(у)=
.
Св-ва: 1) область определ (Д). Д(у)= R;
2) Мн-во значений (Е). Е(у)= .;
3) Ф-ция нечетная у(-х)=-у(х). Док-во: у(-х)=
R(-х)=-
Rх=-у(х);
4) прямая пропорц-ть при к=0 явл постоянной
у=0. При к>0 –возраст; при к<0-убывающая;
5) если задана прямая пропорц-ть у= Rх
и 2 пары соотв-х значений переменных
(
.;
3) Ф-ция нечетная у(-х)=-у(х). Док-во: у(-х)=
R(-х)=-
Rх=-у(х);
4) прямая пропорц-ть при к=0 явл постоянной
у=0. При к>0 –возраст; при к<0-убывающая;
5) если задана прямая пропорц-ть у= Rх
и 2 пары соотв-х значений переменных
(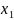 ;
;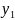 )
и (
)
и (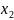 ;
;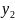 ),
то имеет место равенства:
),
то имеет место равенства:
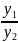 =
= ;
6) График ф-ции у=Rх
есть прямая, проходящая ч/з начало
координат. Обратная пропорц-ть наз
ф-ция, кот м задать формулой вида у=
;
6) График ф-ции у=Rх
есть прямая, проходящая ч/з начало
координат. Обратная пропорц-ть наз
ф-ция, кот м задать формулой вида у= ,
где х-независимая переменная, а R-действ-е
число
,
где х-независимая переменная, а R-действ-е
число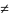 0.
Число R-наз
коэф обратной пропорц-ти и R=ху.
Св-ва: 1) Д(у)=(-
0.
Число R-наз
коэф обратной пропорц-ти и R=ху.
Св-ва: 1) Д(у)=(- ;0)
(0;+
);
2) Е(у)=(-
;0)
(0;+
);
3) ф-ция нечетная у(-х)=-у(х); 4) на интервале
от (0;+
)
ф-ция убывает, при R
0,
возрастает при R
0.
5) основ-е св-во обратной пропорц-ти. Если
задана обратная пропорц-ть у=
и 2 пары переменных (
;
)
и (
;
),
то имеет место равенство
/
=
;0)
(0;+
);
2) Е(у)=(-
;0)
(0;+
);
3) ф-ция нечетная у(-х)=-у(х); 4) на интервале
от (0;+
)
ф-ция убывает, при R
0,
возрастает при R
0.
5) основ-е св-во обратной пропорц-ти. Если
задана обратная пропорц-ть у=
и 2 пары переменных (
;
)
и (
;
),
то имеет место равенство
/
=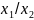 .
Док-во: пусть
=
.
Док-во: пусть
=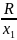 ,
=
,
= ,
тогда
:
=
,
тогда
:
= .
2 величины наход-ся в обратной пропорц-й
зависим-ти, если с увелич-м (уменьшен-м)
в неск раз одной из них вторая уменьш-ся
(увелич-ся) во столько же раз. 6) графиком
обратной пропорц-ти явл гипербола.
.
2 величины наход-ся в обратной пропорц-й
зависим-ти, если с увелич-м (уменьшен-м)
в неск раз одной из них вторая уменьш-ся
(увелич-ся) во столько же раз. 6) графиком
обратной пропорц-ти явл гипербола.
13. Понятие об алгебраической операции. Законы коммутативноти и ассоциативности алгебраических операций. Дистрибутивные законы, связывающие 2алгебраические операции. Нейтральный, поглощающий, симметричный эл-ты.
Определение: Алгебра-ой операцией на мн-ве х наз. отображение (х:у)-> Z кот. ставит каждой упорядоченной паре (Х:У) этого мн-ва третий эл-т Z этого же мн-ва. Закон коммутативности: алгеб. опер. Наз. коммут. Если рез-т ее применения не зависит от порядка компонента, т.е. для 2х эл-ов (а;в)€х вп-ся рав-во а*в=в*а.
Закон ассоциа-ти: алгеб. опер. на мн-ве Х наз. ассоц-ой, если для любых 3 эл-ов выпол-ся рав-во (а*в)*с=а*(в*с). Закон дистрибутивности:
Ноль
это нейтральный эл-т относ-но опер-и
сложения, а 1- относ-но опера-и умножения.
Эл-т е из мн-ва х наз. нейтральным
относ-но
операц-и *, если для любых эл-ов а€х
выпол. Равен-во а*е=е*а=а. Поглощающий
эл-т: Число
0 отыгрывает особую роль не только
отно-но опер-и слож-я, но и относ-но опер-и
умнож-я. А*0=0. Говорят, что 0 явл. поглощ-м
эл-ом относ-но опер-и умнож-я.Во мн-ве х
не м/б 2х разных поглощ-х эл-ов отно-но
опер-и *. Симметричный
эл-т: Пусть
во мн-ве х сущ. нейтрал. эл-т Е отно-но
опер-и *.
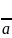 явл.симметр., а если выпол. рав-во
а*а=а*а=l.
явл.симметр., а если выпол. рав-во
а*а=а*а=l.
14. Понятие преобразования плоскости. Перемещения плоскости, их виды.
Рассмотрим геометрич. преобр-ие, при кот. сохр-ся форма и размеры фигур, а меняется их расположение на плоскости. Такие преоб-я наз-ся перемещением. Определ-ие: Преобраз-ие плоскости при кот. кажд. Отрезок АВ переходит в равный ему отрезок А1В1 назыв. перемещением плоскости. Виды плоскости: 1) осевая симметрия с осью е наз-ся такое перем-е плоскости при кот. точки прям. Е отобрах-ся сами на себя а полуплоскости с границей е отобр-ся одна на другую.2) параллельный перенос- отображение плоск-ти на себя, при кот. все точки плос-ти перемещ-ся в одном и том же направлении на одно и то же расс-е. 3) поворот пло-ти- вокруг точки о наз-ся приоб-ие плос-ти, при кот. точеа о отобр-ся сама на себя, а произ-ся т.А плоскости отоб-ся в такую т. А1, что 1) <АОА1=Z, 2)АО=А1О Т. о наз-т центром поворота, если угол задан полож-м числом, то условились поворот произ-ть против часовой стре-ке, если отриц-й, то по часовой стрелке. 4) перемещение – центральной симметрией с центром О наз-ся поворот вокруг т. О на <180. В т. А и А1 лежат на одной прямой кот. прох-т через центрО и по разные стороны от центра: т.к. цент-я симметрия частный случай поворота, то она яв-ся перемещением.
15. Преобразование подобия. Гомотетия.
Останов-ся на преобраз-и, оставляющих неизменными только форму фигур, такие преобразования наз-ся преобр-ми подобия. Св-ва подобия: 1) подобие с коэф-ом 1-ца яв-ся перемещением.Док-во:
2)Для подобия с коэф-ом R сущ-ет обратное подобие с коэф-ом 1/R. Док-во:
3)Композиция подобий есть подобие. Док-во:
Одним из видов подобия на-ся гомотетия. Опред-е: гомот-й с центром О и коэф-ом R=/0наз-ся приобраз-ие плоскости. Частные случаи гомотетии: 1) гомотетия с коэф-ом =1 яв-ся тождественным приобрет-ем Но1=Е.Док-во:
2) гомотетия есть центральная симметрия. Док-во:
16. Теоретико-множественный смысл колич-го натур-го числа и нуля. Отношения равенства и неравенства на мн-ве целых неотриц-х чисел.
Колич-м натур. числом назыв. число, кот. показыв. ск-ко эл-ов содерж. в данном мн-ве. Пусть мн-во А и В таковы, что им соот-т одно и тоже число «а». n(А)=а, n(В)=а. Это значит, что их можно отобразить взаимооднозначно др. на др. и на один и тот же отрезок N ряда чисел. Два мн-ва, кот. можно взаимооднозначно отобразить др. на др. явл. равномощными=» для конечных мн-в утверждение: мн-во А равномощно мн-ву В=утверждению: мн-во А и В содер. одинак. кол-во эл-ов, т.е. им соотв-ет одно и тоже N число. Т.к. любому конеч. мн-ву соот-т лишь 1 N число, то вся сов-ть конеч. мн-в распа-ся на классы равномощных мн-в. Число а=в тогда и только тогда когда они опред-ся равномощ-ми мн-ми.
Св-ва отношения «=»: 1) Рефлексивность а=а, 2) Симметричность если а=в, то в=а, 3) Транзитивность если а=в,в=с, то а=с. Отношение «<»: 1)Число а<в тода и только тогда, если мн-во А собственному подм-ву В1, мн-ва В и n(А)=а, n(В)=в. 2)Число а<в «=» когда сущ-ет N число с, такое что в=а+с
3)а<в,тогда и только тогда, когда отрезок N ряда чисел Nа явл. собств. подм-м отрезка N ряда чисел Nв.
Св-ва:1) антирефлекс. а</а, 2) антиссиметр. a<в=»/в<а, 3) транзитивность а<в, в<с=»а<c. Т.о. отношение «<» явл. отношением строгого линейного порядка.
