Спектр гармонического процесса
формально
этот спектр не существует:
,
т.е. функция не интегрируема, следовательно,
нет спектра Фурье. Но иногда очень
хочется, чтобы спектр был. Пусть спектр
существует, тогда сигнал можно восстановить
с помощью обратного преобразования.
Рис 22
Воспользуемся
свойством
-функции:
-ведет
себя как
-функция
действительно:
Спектр
синуса можно представить, как
-функцию:
Рис.23
Спектр синуса, ограниченного во времени
Рис.24
,
Спектр процесса дискретизованного во времени
-прямое
преобразование непрерывного спектра
-
обратное преобразование
переходим:
,
i-целое
рассмотрим:
,т.е.
представляем спектр процесса в виде
бесконечной суммы.
.
Рис.25
,
где
-частота
дискретизации
как связан непрерывный спектр процесса с дискретным спектром? Дискретный спектр – это повторение непрерывного спектра много раз.
Рис.26
Связь
между этими спектрами:
- формула иллюстрирует дискретный
спектр.
Оценим,
к чему это приводит:
Рис.27
Средние части не изменяются, т.е. повторяются без искажений:
Это
когда
(по
теореме Котельникова)
Пусть
условие теоремы Котельникова не
выполняется:
Рис.28
Получаем искажённый сигнал. Искажение не контролируемо, т.е. искажение нельзя восстановить.
,
где
-
детерминируемая функция, следовательно,
что
-детерминированный спектр. Множество
реализации
,
где
.
Этой реализации соответствует реализация
спектра
.
-
спектр мощности случайного процесса,
где
-
корреляционная функция.
,
где
и 2) представления эквивалентны.
Рис.29
,где
-
не случайна.
Фильтрация процесса
Рассмотрим
линейный фильтр:
,
где
-
импульсная функция
.
Рис.30
Каждый фильтр может быть представлен либо во временной области, либо в частотной.
В
частотной:
,
Рис.31
Рис.32
ФНЧ – фильтр низкой частоты
Рис.33
ФВЧ – фильтр высокой частоты
Рис.34.
Полосный фильтр
Рис.35
Полосно-задерживающий фильтр
Пусть
есть спектр
,
Для
случайного процесса:
,
где
и
-
случайны.
Методы дискретизации сигналов
,
где i=…,-2,-1,0,1,2,…
=
const,
тогда будет равномерная дискретизация.
,
=
var
(переменная) – это уже не равномерная
дискретизация.
-
это основа адаптивной дискретизации.
Рис.36
Адаптивная дискретизация подстраивается под текущую скорость процесса.
Стохастическая дискретизация Берем случайные интервалы.
Цель: сократить отсчёты при стохастической и адаптивной дискретизации.
Основные задачи:
1)
выбор
:
с целью восстановления сигнала;
оценка параметров сигнала.
Восстановление сигнала:
восстановленная
функция:
,
т.е. имея выборку сигнала, строим функцию
,
но есть ошибка восстановления
.
,
при
.
Квадратичная
ошибка:
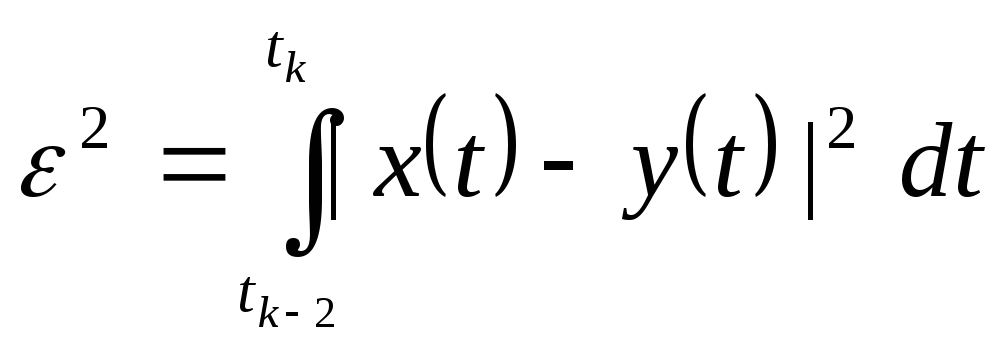
Оценка параметров сигнала
Рис.37.
Нижний сигнал – клипированный, по нему можно дать оценку.
При восстановлении сигнала метод дискретизации основывается на частотных представлениях. При оценке параметров сигнала метод основывается на оценке ошибки восстановления сигнала.
Теорема
Котельникова:
есть непрерывный процесс
с ограниченным спектром (ограничен
частотой
).
Этот
непрерывный процесс может быть
восстановлен по своим дискретным
отсчётам, взятым с частотой
.
Смысл
теоремы Котельникова: можно построить
,
возьмём непрерывный фильтр (идеальный
частотный фильтр) с частотной
характеристикой:
Рис.38
И как бы вырезаем один кусочек:
Рис.39
Во
временной области:
-непрерывный.
т.е. восстановление сигнала: пропускаем дискретизованный сигнал через фильтр. Построим импульсную функцию для фильтра:
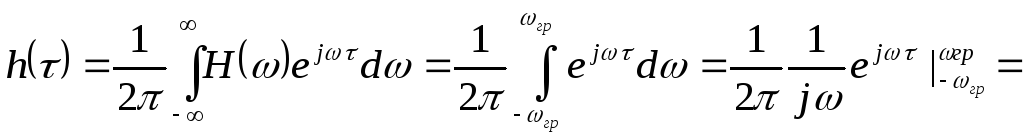
Подставив,
получим:
.
Итак,
ряд Котельникова это:
Таким
образом, при
- полное восстановление сигнала, но есть
и ограничения:
1)
,
при
,
Рис.40
Рис.41
Спектр
расширяется, следовательно, нельзя
точно выбрать
.
Существуют методы выбора частоты дискретизации:
:
приближённо выполняется
.
Сделаем
оценку:
,
где
,
т.е. сводим к
и работаем с ней.
процесс надо восстановить с помощью бесконечного ряда.
Берём
,
где N
- количество точек.
Рис.42
,
т.к.
.
При
ограниченной реализации:
следовательно, ряд – это конечная сумма,
тогда имеем отклонения.
Ошибка восстановления: в дискретных точках ошибка равна нулю.
Рис.43
Эта ошибка мало контролируема.
Вывод:
“минусы”: восстановление по ряду Котельникова приводит к ошибкам, которые трудно оценить, т.е. Теорема Котельникова не гарантирует хороших результатов.
”плюсы”: можно восстанавливать спектральные т статистические свойства сигнала, т.е. для исследования сигнала.