Эффекты подмена частот

, ,

Когда это условие нарушается, идёт эффект подмена частот.

Пусть есть ,

Спектр такого процесса:

Рис.44

, где F – частота Найквиста.

Первый вариант: рассмотрим : ,

Система будет реагировать:

Таким образом, восстанавливается сигнал, как сигнал с частотой , т.е. цифровой системе всё равно.

Пример: =20Гц, =100Гц

20Гц, 120Гц, 220Гц.

Второй вариант: берём

Рис.45

Пример: =100Гц, =50Гц, =50+20=70Гц, =50-20=30Гц

Диаграмма порождения частот

0,25F 1.75F

2.25F 0.25F 3.75F 0.25F

4.25F 5.75F

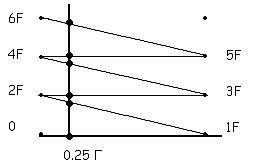
Рис.46

Методы дискретизации, основанные на критерии качества восстановления сигнала

Пусть есть n+1 точек, можно взять полином n-порядка:

- выбираем и строим полином, который удовлетворяет системе уравнений:

результатом решения этой системы будет полином Лагранжа.

Его особенности: он проходит через точки отсчёта, т.е. находим

Рис.47

Задача – оценить :

- определяется остаточным членом полинома Лагранжа.

Введём ,

Если - целое: , т.е. попадаем в значение отсчёта.

Если -нецелое: попадаем приблизительно в середину между отсчётами.

Полином можно представить через нормированное время:

ошибка: - в частотной области;

- во временной области.

Выражение для остаточного члена:

Максимальное значение производной n+1-порядка:

Рис.48

Задача: найти .

База: порядок полиномами количество используемых точек.

1. n=0

Рис.49

Тогда: , где - точность,

, где , при

Здесь берём полином, который из точки строится вперёд, т.е. экстраполяция, а можно сделать интерполяцию, т.е. – строим назад:

Рис.50

В итоге восстановленный полином будет ступенчатым, но ступенчатая функция не самая лучшая.

Рис.51

Полином Лагранжа не самый хороший, есть полином Чебышева, он минимизирует максимальную ошибку.

2. n=1 – ведём аппроксимацию с помощью линий.

Рис.52

,

, , ,

Рассмотрим пример. , дискретизируем этот сигнал.

n=0: пусть -абсолютная ошибка, , . Здесь разница в 31,4 раза, следовательно, невыгодная.

n=1: ,

Вывод: с ростом порядка полинома будет уменьшаться.

Таблица: - коэффициент уменьшения частоты дискретизации.

	0,1	0,01	0,001
	8,9	28,3	89,5
	11,6	53,9	250,0
	12,5	67,0	395,0
	12,7	80,5	504,0

Брать полином выше второго порядка не имеет смысла брать, т.к. для каждой точки увеличивается число операций. Плюс в том, что заранее оценивается погрешность. Т.к. полином Лагранжа не оптимизирован, то можно взять полиномы «лучше».

Принципы адаптивной дискретизации

Пусть процесс не стационарный, например, меняется его скорость изменения

Рис.53

Производная: . Здесь используется дискретизация:

1. - невыгодно, т.к. нужна слишком частая дискретизация.

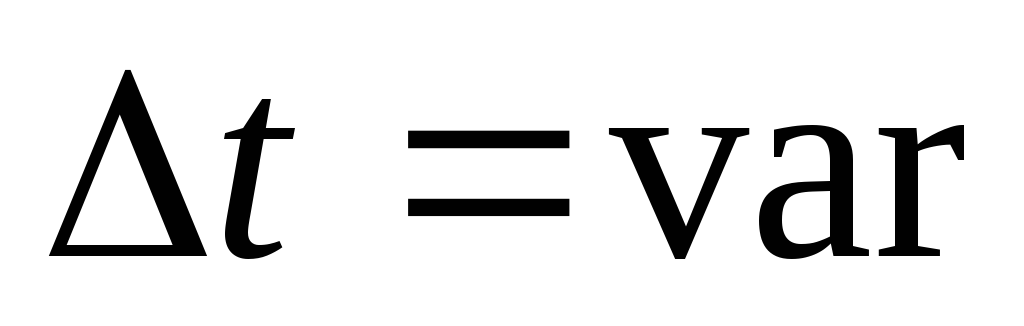2. - здесь уже существуют методы выбора .

Адаптивная дискретизация

1. 0-ого порядка.

Выбираем момент и отсчёт .

, при - прогноз 0-ого порядка.

Строим функцию, которая даёт текущую ошибку:

Рис.54

если это условие выполняется, то следующий отсчёт не берётся, если в какой-то следующий момент времени будет:

,

тогда берём следующий отсчёт и т.д.

здесь количество информации увеличивается, т.к. надо запоминать текущую разницу: .

Этот метод выигрывает, когда: выигрыш по отсчётам - .

q – количество информации =,

выигрыш по информации -

2) 1-ого порядка.

Рис.55

надо передавать значения: .

В качестве оценки: ,

Тогда передаём:

Выигрыш по отсчётам: .