4. Законы распределения

4.1. Элементы теории вероятности при расчете надежности.

Отказы носят случайный характер, а сам отказ трактуют как случайное событие.

Вероятность события А – отношение числа возможных результатов испытания, благоприятствующих появлению события А и общему числу всех возможных результатов: .

Случайное событие называют достоверным если в результате испытания онообязательно происходит. Случ. Событие которое заведомо не может произойти, называют невозможным.

Случайные события м.б. несовместными или совместными, независимыми или зависимыми.

Несовместными – называется 2 таких случайных события которые не могут произойти в одном и том же испытании.

Независимыми – называют такие события, когда появление одного из них не влияет на появление других.

При решении задач надежности используют такое понятие частоты события : (А), которая представляет собой отношение результатов испытания, в которых событие А появилось к общему числу n результатов испытания:

При неограниченном увеличении «n»  стремится к Р и является её приближенной оценкой. Частоту () называют статистической вероятностью.

Теоремы теории вероятности в рамках задач надежности.

1. Сложение вероятностей несовместных событий: вероятность  несовместных событий =  их вероятностей и равна вероятности того, что произойдет хотя бы одно из них.

Два несовместимых случайных события образующих полную группу т.е.

называются противоположными.

, где - событие, противоположное А

2. Умножение вероятностей независимых событий: вероятность появления таких событий равна П их вероятностей

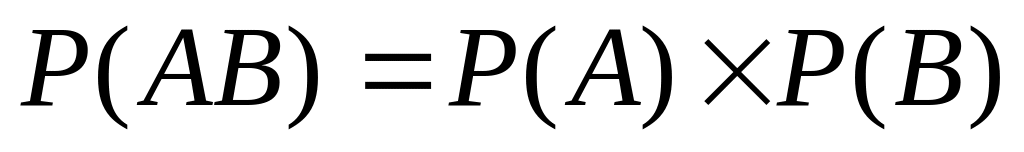
3. Умножение зависимых событий (вероятность появления одного из них зависит от появления или не появления другого). Для этого пользуются «условной вероятностью»: 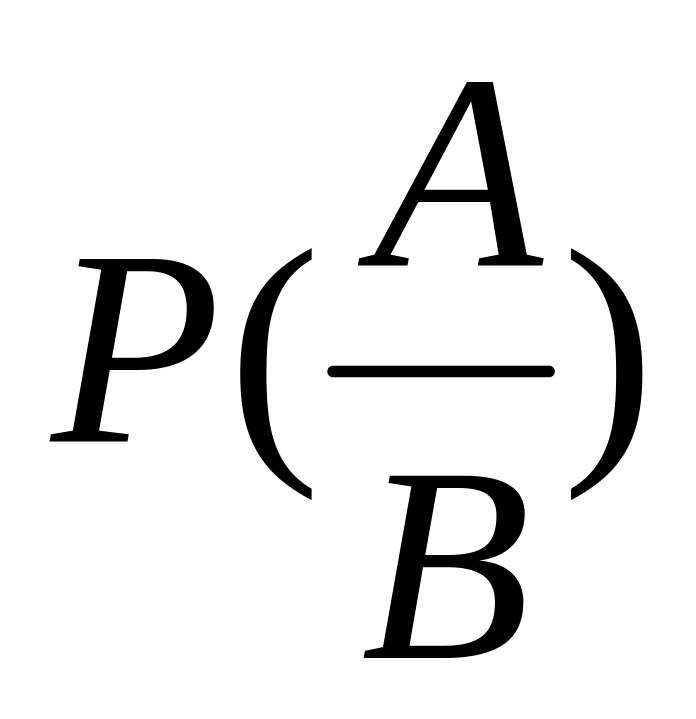- вероятность появления события А, при условии что событие В, имеющие Р(В)>0 уже произошло.

Случайные величины

С.в. называется величина, которая в результате испытаний начинает принимать 1 из возможных, заранее не известных значений.

С.в. называется дискретной, если она может принимать конечное или бесконечное счетное множество значений, т.е. если эти значения могут быть пронумерованы в количественном порядке.

С.в. называется непрерывной, если она может в результате испытания принять любое значение в 1 или нескольких заданных интервалах. Эти значения образуют несчетное бесконечное множество (континуум).

Для полной характеристики с.в. необходимо знать законы ее распределения.

Законом распределения – называется зависимость, устанавливающая связь между возможными значениями случайной величины и их вероятностями. Может быть задан таблично, графически или аналитически.

Закон распределения непрерывной случайной величины задают функцией распределения F(x) (интегральной функцией распределения), определяющей вероятность того, что случайная величина Х в результате испытаний примет значение, меньше х, т.е.

В надежности отказ представляется, как событие, состоящие в том, что

<t => F(t) наработки  имеет физический смысл вероятности отказа объекта за время меньшее t :

Тогда вероятность безотказной работы может быть найдена:

Функция Р(t) называется функцией надежности.

Наряду с F(t), применяют другую функцию, называемую “плотностью распределения” или “плотностью вероятности”. По её характеру можно судить о физической сущности и характере отказов.

Плотность распределения

Свойства f(x):

1. ;

2. 

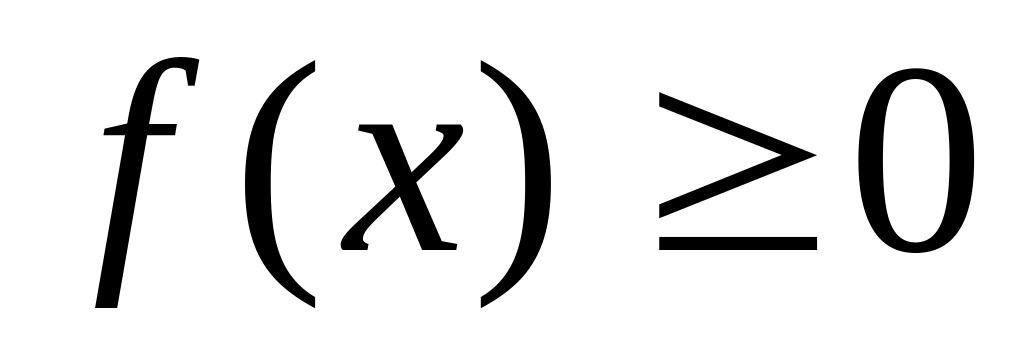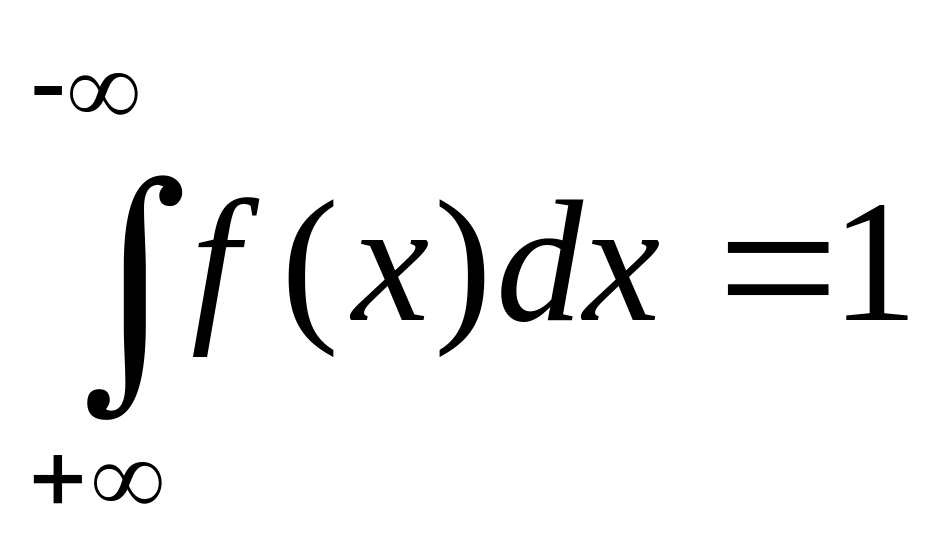
При расчетах надежности часто пользуются менее полными, но более простыми характеристиками с.в.: м.о. и Dx.

М.о. дискретной случайной величины называют П всех её возможных значений на их вероятности:

Для непрерывных величин:

М.о. приблизительно равно арифметическому значению с.в.:

Центрированной с.в., соответствующей величине Х, называется отклонение с.в. Х от м.о.:

Дисперсией с.в. Х называют м.о. соответственной центрированной величины.

Dx характеризует степень рассеивания с.в. относительно м.о.

Формулы вычисления Dx:

• для дисперсных с.в.:

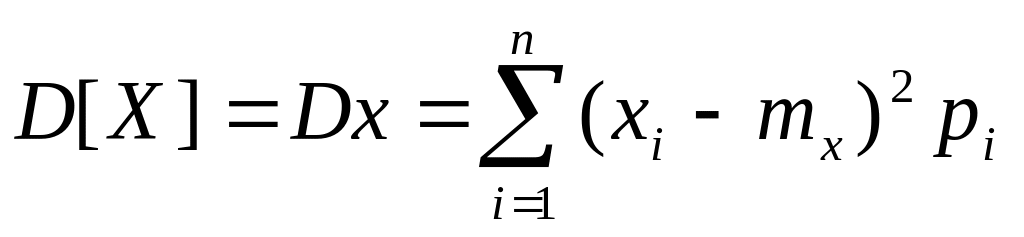
• для непрерывных с.в.:

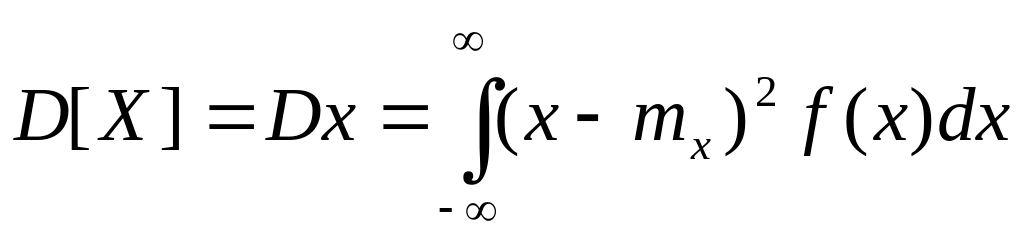
Для оценки рассеяния с.в. используется также среднеквадратичное отклонение:

4.2. Законы распределения наработки до отказа.

1 из необходимых операций – определение на основании статических данных закона распределения различной величины.

1. Экспоненциальный закон

Характеризуется плотностью распределения наработки (времени) до отказа (плотностью вероятностей отказов) , где  - интенсивность отказов (параметр закона распределения).

Функция распределения:

Вероятность отказа за время t:

Вероятность безотказной работы (функция надежности):

Средняя наработка (время работы) до возможного отказа равна м.о. наблюдаемых значений наработки до отказа (времени безотказной работы) объекта:

Дисперсия наработки до отказа:

среднеквадратичное отклонение до отказа:

То – среднее время безотказной работы.

Интенсивность отказов:

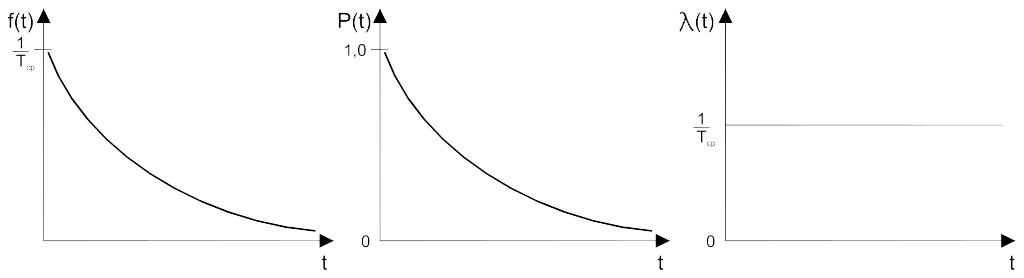
Экспоненциальный закон может использоваться и по отношению ко времени восстановления:

g(t) – плотность распределения времени восстановления,

 - интенсивность (параметр потока восстановления)

tв – среднее время восстановления

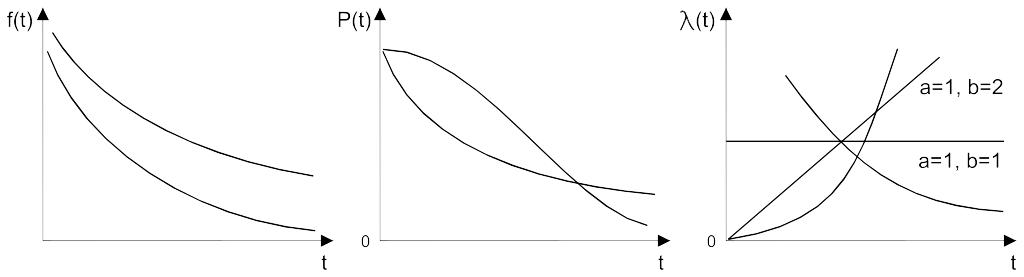
2. Закон Вейбусла, имеет 2 параметра и задается плотностью распределения вероятностей наработки до отказа:

и функцией распределения:

а – параметр масштаба (по оси х);

b – параметр формы (острота и симметрия)

а и b всегда >0

Функция надежности: ;

Вероятность отказа: ;

Интенсивность отказов:

Широкое распр-ие, т.к. подбирая значения параметров можно добиться более полного соответствия.

При b=1, распределение B переходит в exp.

Хорошо описывает усталостные отказы: отказы объектов, состоящих из последовательно соединенных дублированных элементов и т.п.

3. Нормальный закон

Хорошо описывает распределение вероятностей до отказа объектов, когда она зависит от большого числа однородных по влиянию случайных факторов, влияние каждого из которых незначительно. Характерны для постепенных отказов.

Плотность распределения:

Функция распределения:

где t0 – м.о. наработки до отказа,  - среднеквадратичное отклонение наработки до отказа.

t0 – характеризует отклонение центра группирования по оси х;  - форму кривой f(t).

Характерным признаком нормального распределения – монотонное возрастание с момента начала эксплуатации объекта.

Вероятность отказа (0,t):

Вероятность безотказной работы:

Ос-ть нормального распределения – 99,73% случайной величины укладывается на участке .

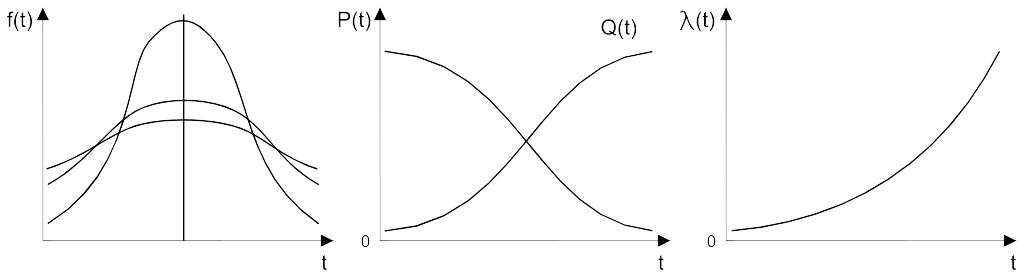
4. Закон гамма – распределения.

Распределение наработки до отказа резервированных объектов, элементы которых имеют экспоненциальное распределение наработки до отказа.

Плотность распределения:

Если k – целое число , то функция раскрывается:

где k – параметр формы (число элементов или число отказов),

0 – масштабный параметр (интенсивность отказов во время испытания).

Вероятность безотказной работы:

k-1 – число резервных элементов.

Средняя наработка до k-го отказа не резервируемого объекта при 1 испытании = м.о. набл. Значению наработки до отказа:

Дисперсия :

Интенсивность отказов:

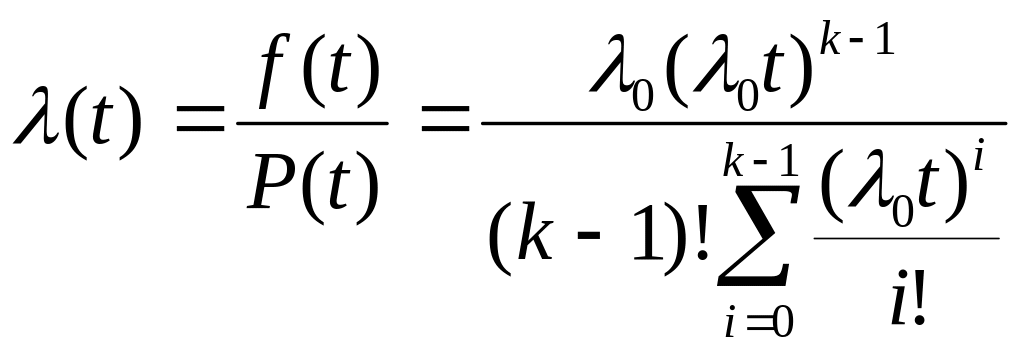
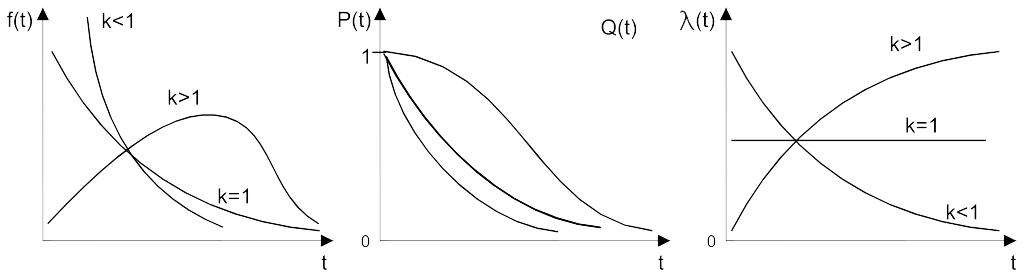
При k=1 закон гамма распределения превращается в экспоненциальный,

k>1 (t) ; k<1 (t) .

Гамма-распределение может хорошо описывать наработку до отказа (время до возможных отказов) сложных систем, если имеют место мгновенные отказы элементов в начальной стадии эксплуатации или в процессе приработки систем.

Наиболее универсальным является закон Вейбусла, т.к.:

1. Экспоненциальный и некоторые другие законы являются частными случаями закона Вейбусла при соответствующем коэффициенте формы;

2. Усеченное нормальное распределение описывается хорошо распределением закона Вейбусла при d>3,5.

3. Логарифм распределения аппроксимируется распределением закона Вейбусла так, что для получения стат. различия между ними необходимо больше 1000 испытаний.