Раздел 3. Метод Ляпунова. Алгоритм.
Ляпунов предложил простой и очень эффективный метод построения периодических решений для достаточно малых значений постоянной с решения системы (1.8). Алгоритм Ляпунова использует аналитичность искомых решений по параметру с и дает правило построения решений в форме рядов специального вида, разложенных по степеням этого параметра.
Таким образом, на основании теоремы в разделе 1, решение системы уравнений (1.8) можно искать в виде:
, 
.
но это невозможно, так как период решения Т неизвестен. Тогда Ляпунов предложил видоизменить масштаб времени так, чтобы решения полученной системы имели фиксированный период, не зависящий от с (например, равный ).
Обратим внимание на формулу (1.24). Она показывает, что если ввести замену
(3.1)
то
период колебаний по переменной
будет равен
.
Сделав в системе уравнений (1.8) замену
(3.1), получим
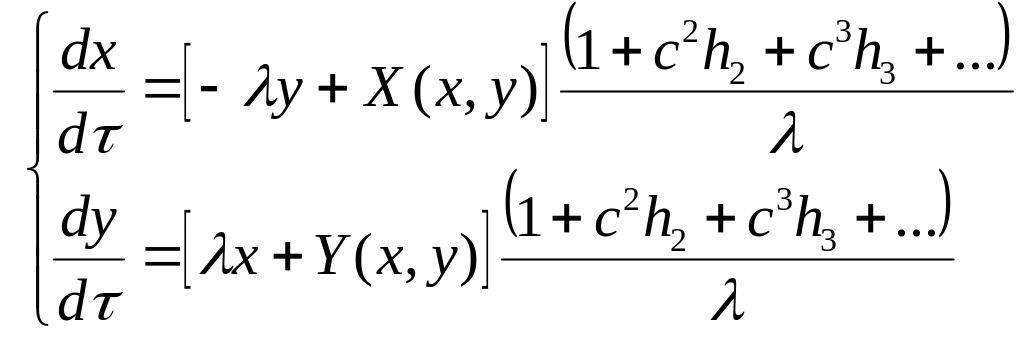(3.2)
Так
как правые части системы (3.2) мы умножили
на аналитические функции параметра
,
то решение этой системы, так же как и
системы (1.8), аналитические по
и для любого достаточно малого
периодические по
.
Но период по независимой переменной
теперь уже фиксирован, он равен
.
Периодические решения системы (3.2) будем искать в виде рядов
, 
.
(3.3)
Подставим
ряды (3.3) в систему уравнений (3.2) и сравним
коэффициенты при одинаковых степенях
параметра
.
Функции
и
будут удовлетворять следующей системе
уравнений:
,
. (3.4)
В самом деле, функции и , будучи аналитическими функциями своих переменных, таковы, что их разложение начинается с членов второго порядка малости. Следовательно, при подстановке в эти функции рядов (3.3) функции и не будут содержать членов, линейных относительно . Начальные значения для системы (3.2) определены равенствами (1.13)
:
, 
.
Следовательно,
функции
и
будут соответствовать следующим
начальным условиям:
:
, 
,
,
,
где i
=2,3…
(3.5)
Функции
и
будут удовлетворять системе уравнений
(3.6)
где
и
─ квадратичные члены разложения функций
и
по степеням параметра
.
Так как
и
─ аналитические функции переменных
и
,
причем их разложение начинается с
квадратичных членов, то
и
являются квадратичными формами переменных
и
.
Точно
так же каждая пара функций
и
,
входящая в разложение (3.3), определяется
системой уравнений
(3.7)
причем
функции
и
будут содержать величины
и
только тех номеров
,
которые меньше чем
.
Кроме
того, функции
и
будут содержать величины
,
причем
Заметим, что величины
входят в правые части (3.7) только уравнений
относительно
и
,
для которых
:
(3.8)
и т. д.
Из
уравнений (1.13) следует, что функции
и
при
удовлетворяют начальным условиям
, 
. (3.9)
Вернемся
снова к уравнениям (3.2). Хотя числа
нам неизвестны заранее, но они на
основании теоремы Ляпунова определяются
однозначно для данной системы и не
зависят от параметра
,
ни от начальных условий.
Далее
члены рядов (3.3) также определяются
однозначно, причём
и
─ периодические функции переменного
периода
.
В самом деле,
и
─ периодические функции, следовательно,
(3.10)
Так как функции и не зависят от параметра , а равенства (3.10) справедливы для любого малого , то
,
.
Таким образом, мы можем утверждать заранее, что функции и , которые определяются как решение задачи Коши (3.9) для системы уравнений (3.7), будут периодическими функциями времени периода . С другой стороны, уравнения (3.7) относятся к виду
,
, (2.11)
где
, 
являются
периодическими функциями времени,
поскольку они определяются периодическими
функциями
…,
,
,
…,
.
Система вида (2.11) имеет периодическое
решение тогда и только тогда, когда
функции
удовлетворяют условиям
На этом основании можно сформулировать следующее вспомогательное утверждение:
функции
,
и числа
всегда удовлетворяют условиям (3.11)
