
- •Часть 2
- •Часть 2
- •Задания к контрольной работе 3
- •Методические указания к контрольной работе 3
- •2. Предельный признак сравнения.
- •5. Интегральный признак Коши.
- •1) , 2) (Последовательность убывает), тогда знакочередующийся ряд (4) сходится.
- •Однородное уравнение.
- •Линейным уравнением первого порядка называется уравнение вида , (11)
- •5. Уравнением Бернулли называют уравнение следующего вида
- •Уравнение со специальной правой частью второго типа.
- •Метод вариации произвольных постоянных.
- •Задания к контрольной работе 4
- •Методические указания к контрольной работе 4
- •Число размещений .
- •Число перестановок .
- •Число сочетаний .
- •Формула полной вероятности.
- •Формула Байеса.
Методические указания к контрольной работе 3
Задание 1. Криволинейный интеграл первого рода.
Пусть гладкая
кривая
в пространстве задана параметрически
равенствами
 ,
где параметр
,
где параметр
 меняется
в пределах
меняется
в пределах
 ,
,
 ,
то есть
,
то есть
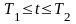 .
Предположим, что на этой кривой
распределена масса или электрический
заряд с плотностью
.
Предположим, что на этой кривой
распределена масса или электрический
заряд с плотностью
 .
Тогда масса всей кривой или величина
суммарного заряда определяется следующим
интегралом
.
Тогда масса всей кривой или величина
суммарного заряда определяется следующим
интегралом
 ,
который называют криволинейным интегралом
первого рода.
,
который называют криволинейным интегралом
первого рода.
Вычисляется этот интеграл с помощью определённого интеграла по следующей формуле
=
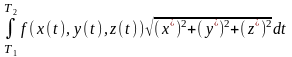 .
.
Основными свойствами криволинейного интеграла первого рода являются линейность и аддитивность:
1)
 ,
,

 +
+
 ;
;
2) если кривая
состоит из двух частей
 и
и
 ,
тогда
=
,
тогда
=
 +
+
 .
.
Пример.
Найти массу кривой
 ,
,
с
плотностью
=
 .
Находим
.
Находим

 ,
,
 =
=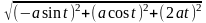 =
= .
Следовательно, масса всей рассматриваемой
кривой
.
Следовательно, масса всей рассматриваемой
кривой
 = =
= = =
=
 =
=
 =
=
 =
=
 =
=
 .
.
Криволинейный интеграл второго рода
Пусть в каждой
точке кр ивой
задан вектор (например, сила)
 .
Тогда работа, совершаемая этой силой
по перемещению материальной точки из
точки
.
Тогда работа, совершаемая этой силой
по перемещению материальной точки из
точки
 с координатами
с координатами
 в точку
с координатами
в точку
с координатами
 определяется интегралом
определяется интегралом
 =
=
 ,
где
,
где
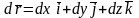 .
Этот интеграл называется криволинейным
интегралом второго рода и вычисляется
по формуле
=
.
Этот интеграл называется криволинейным
интегралом второго рода и вычисляется
по формуле
=
 .
.
Кроме свойств
линейности и аддитивности криволинейный
интеграл второго рода обладает следующим
свойством: если точка движется по кривой
в обратном направлении от точки
к точке
,
тогда интеграл меняет знак. Если
обозначить
 движение вдоль кривой
в направлении возрастания параметра
от
точки
к точке
,
а
движение вдоль кривой
в направлении возрастания параметра
от
точки
к точке
,
а
 движение в обратном направлении, то
движение в обратном направлении, то
 =
–
=
– .
.
Пример.
Вычислим работу силы
 вдоль замкнутого контура треугольника
O(0,0,0),
(1,1,1),
(1,1,0),
О(0,0,0). По свойству аддитивности
=
вдоль замкнутого контура треугольника
O(0,0,0),
(1,1,1),
(1,1,0),
О(0,0,0). По свойству аддитивности
=
 +
+ +
+ .
Составим параметрические уравнения
прямых
.
Составим параметрические уравнения
прямых
 Направляющий вектор прямой
Направляющий вектор прямой
 имеет координаты (1,1,1). Следовательно,
её каноническое уравнение имеет вид
имеет координаты (1,1,1). Следовательно,
её каноническое уравнение имеет вид
 ,
а параметрическое уравнение:
,
а параметрическое уравнение:
 где
параметр
меняется от 0 до 1 при движении в направлении
.
Аналогично,
где
параметр
меняется от 0 до 1 при движении в направлении
.
Аналогично,
получим
уравнение прямой
 :
:
 где
параметр
меняется от 1 до 0 при движении в направлении
,
и уравнение прямой
где
параметр
меняется от 1 до 0 при движении в направлении
,
и уравнение прямой
 :
:
 где
параметр
меняется от 1 до 0. Таким образом,
=
где
параметр
меняется от 1 до 0. Таким образом,
= =
= ,
=
,
= ,
а интеграл
=
,
а интеграл
= .
Следовательно, искомая работа
=
.
Следовательно, искомая работа
=
1
 =
0.
=
0.
Задание 2. Двойной интеграл.
Пусть функция
 непрерывна в ограниченной области
непрерывна в ограниченной области
 (омега) на плоскости XOY.
Если в области
распределена масса или электрический
заряд с плотностью
,
тогда масса всей области
или суммарная величина заряда вычисляется
с помощью интеграла
(омега) на плоскости XOY.
Если в области
распределена масса или электрический
заряд с плотностью
,
тогда масса всей области
или суммарная величина заряда вычисляется
с помощью интеграла
 ,
который называется двойным интегралом
от функции
по области
.
,
который называется двойным интегралом
от функции
по области
.
Основными
свойствами двойного интеграла являются:
1) линейность:
 ,
где
,
где
 –
постоянная,
–
постоянная,
 =
=
 2)
аддитивность: если область
2)
аддитивность: если область
 (область
состоит из двух частей, котрые могут
пересекаться по кривой), тогда
=
(область
состоит из двух частей, котрые могут
пересекаться по кривой), тогда
=
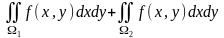 .
.
Вычисление двойного интеграла сводится к повторному интегрированию, то есть к двукратному вычислению определённого интеграла.
Пусть область
является криволинейной трапецией
относительно оси OX, то
есть является частью плоскости,
ограниченной прямыми
 ,
,
 (
( )
и кривыми
)
и кривыми
 ,
где
,
где
 для всех значений
для всех значений
 .
Тогда
.
Тогда
=
 .
.
Сначала
вычисляется внутренний интеграл в
предположении, что
является функцией одной переменной
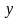 (
( считается
постоянной), а затем вычисляется интеграл
от функции одной переменной
по промежутку
считается
постоянной), а затем вычисляется интеграл
от функции одной переменной
по промежутку
 .
.
Пример.
Вычислим
 ,
где область
является частью
,
где область
является частью
плоскости,
ограниченной кривыми
 .
Из равенства
.
Из равенства

находим
точки пересечения этих кривых
 .
Следовательно,
.
Следовательно,
 .
Так как
.
Так как
 для всех
для всех
 ,
то кривая
ограничивает область интегрирования
сверху, а кривая
снизу. Таким образом, имеем
=
,
то кривая
ограничивает область интегрирования
сверху, а кривая
снизу. Таким образом, имеем
=
 =
=
 =
=

 =
=
 =
=
 =
=
 =
=
 .
.
Если функция
≡ 1, тогда
=
 – площадь области
.
– площадь области
.
Пример.
Вычислим площадь фигуры, ограниченной
линиями
 (смотри предыдущий пример). Имеем,
(смотри предыдущий пример). Имеем,
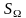 =
=
=
=
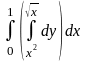 =
=
= =
=
 =
1.
=
1.
Если область
не является криволинейной трапецией
относительно оси OX, тогда
разбивается прямыми, параллельными оси
OY, на части
 каждая из которых является криволинейной
трапецией относительно оси OX.
После этого вычисляют двойной интеграл,
используя свойство аддитивности
=
каждая из которых является криволинейной
трапецией относительно оси OX.
После этого вычисляют двойной интеграл,
используя свойство аддитивности
=
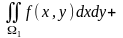
 .
.
Пример.
Вычислим
 ,
если область
ограничена линиями x=0,
y=x,
y=x+1,
y=2. Эта область не
является криволинейной трапецией
относительно оси OX, но
прямая x=1 разбивает
эту область на две части
,
если область
ограничена линиями x=0,
y=x,
y=x+1,
y=2. Эта область не
является криволинейной трапецией
относительно оси OX, но
прямая x=1 разбивает
эту область на две части
 ={(x,y):
0
={(x,y):
0
 },
},
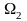 ={(x,y):
1
={(x,y):
1
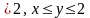 },
каждая из которых является криволинейной
трапецией. По свойству аддитивности
двойного интеграла имеем
=
},
каждая из которых является криволинейной
трапецией. По свойству аддитивности
двойного интеграла имеем
=
 +
+ =
=
 +
+
 =
=
 +
+
 =
=
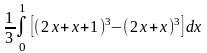 +
+
 =
=
 +
+
 =
=
 +
+
 =
=
 +
+
 =
=
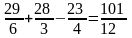 .
.
Пусть область
интегрирования
является криволинейной трапецией
относительно оси OY, то
есть является частью плоскости,
ограниченной прямыми y=c,
y=d
(c < d)
и кривыми
 ,
где
,
где
 для
всех значений
для
всех значений
 .
Тогда двойной интеграл вычисляется
повторным интегрированием следующим
образом
.
Тогда двойной интеграл вычисляется
повторным интегрированием следующим
образом
=
 .
.
Сначала
вычисляется внутренний интеграл в
предположении, что
является функцией одной переменной x
(y считается
постоянной), а затем вычисляется интеграл
от функции одной переменной y
по промежутку
 .
.
Пример.
Вычислим
 ,
если область
ограничена линиями y
= 1, y=x,
y=x+1,
y=2. Эта область не
является криволинейной трапецией
относительно оси OX, но
является трапецией относительно оси
OY. следовательно,
=
,
если область
ограничена линиями y
= 1, y=x,
y=x+1,
y=2. Эта область не
является криволинейной трапецией
относительно оси OX, но
является трапецией относительно оси
OY. следовательно,
=
 =
=
 =
=
 =
=
 =
=
 =
=
 =
=
 .
.
Переход к полярным координатам в двойном интеграле
Пусть точка M
в декартовой системе имеет координаты
x,y.
Тогда полярным радиусом этой точки
называют расстояние от точки M
до начала координат или длину радиус –
вектора
 этой
точки, а полярным углом называют угол,
который радиус – вектор
образует
с осью OX. Полярный радиус
обозначают r, а полярный
угол
этой
точки, а полярным углом называют угол,
который радиус – вектор
образует
с осью OX. Полярный радиус
обозначают r, а полярный
угол
 .
Связь декартовых координат точки с
полярными осуществляется равенствами
.
Связь декартовых координат точки с
полярными осуществляется равенствами
 .
.
Если область интегрирования является кольцевым сектором, то есть в декартовых координатах задаётся системой неравенств

тогда
в полярной системе координат эта область
будет являться прямоугольником
 ,
где полярные углы
,
где полярные углы
 определяются
из равенств
определяются
из равенств

Переход в двойном интеграле от декартовых координат к полярным координатам осуществляется по формуле
 ,
,
которая, в случае, когда область интегрирования является кольцевым сектором, принимает следующий вид
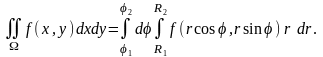 (1)
(1)
Пример.
Вычислим двойной интеграл
 ,
если область интегрирования
задана неравенствами
,
если область интегрирования
задана неравенствами

В этом случае
имеем
 ,
а
,
а
 Следовательно,
Следовательно,
 ,
и рассматриваемый интеграл, согласно
формуле (1), будет равен
=
,
и рассматриваемый интеграл, согласно
формуле (1), будет равен
=
 = (так как внутренний интеграл не зависит
от
)
=
= (так как внутренний интеграл не зависит
от
)
=
 = (после замены переменной
= (после замены переменной
 )
=
)
=
 =
=
 =
=
 =
=
 .
.
Тройной интеграл
Если в области
V трёхмерного
пространства распределена масса или
электрический заряд с плотностью
,
тогда масса этой области или суммарный
электрический заряд определяются с
помощью тройного интеграла
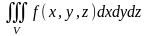 ,
который обладает теми же свойствами,
что и двойной интеграл (линейность,
аддитивность и т.д.).
,
который обладает теми же свойствами,
что и двойной интеграл (линейность,
аддитивность и т.д.).
Вычисление
тройного интеграла, также как и двойного,
производится с помощью повторного
интегрирования. Пусть область V
является цилиндрической относительно
оси OZ: ограничена снизу поверхностью
 (нижнее
основание), ограничена сверху поверхностью
(нижнее
основание), ограничена сверху поверхностью
 (верхнее основание),
(верхнее основание),
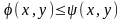 ,
а образующая параллельна оси OZ. Тогда
справедливо равенство
,
а образующая параллельна оси OZ. Тогда
справедливо равенство
 (2)
(2)
где
 –
проекция цилиндра V
на плоскость XOY.
–
проекция цилиндра V
на плоскость XOY.
Пример.
Вычислим тройной интеграл
 ,
если область интегрирования V
является тетраэдром, который ограничен
плоскостями
,
если область интегрирования V
является тетраэдром, который ограничен
плоскостями

 .
.
Очевидно,
область V является
цилиндрической относительно оси OZ,
которая ограничена снизу плоскостью
 ,
ограничена сверху плоскостью
,
ограничена сверху плоскостью
 ,
а проекцией
тетраэдра на плоскость XOY является
треугольник, ограниченный прямыми
,
а проекцией
тетраэдра на плоскость XOY является
треугольник, ограниченный прямыми


 Согласно формуле (2) имеем
=
Согласно формуле (2) имеем
=
 = (переходим к повторному интегрированию
в полученном двойном интеграле) =
= (переходим к повторному интегрированию
в полученном двойном интеграле) =
 = (вычисляем внутренний интеграл) =
= (вычисляем внутренний интеграл) =
 =
=
 = (вычислим внутренний интеграл)
= (вычислим внутренний интеграл)
 =
= =
=
 =
=
 .
.
Тройной интеграл
используется для вычисления объёма
пространственных тел, который равен
 .
.
Пример.
Вычислим объём части цилиндра
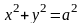 ,
заключённой между плоскостями
,
заключённой между плоскостями
 ,
,
 .
.
По условию,
данное тело V ограничено
снизу плоскостью
 ,
а сверху плоскостью
,
а сверху плоскостью
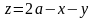 .
Проекцией этого тела на координатную
плоскость XOY является круг
.
Проекцией этого тела на координатную
плоскость XOY является круг
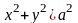 .
Следовательно, искомый объём равен
=
.
Следовательно, искомый объём равен
=
 =
=
 =
=
 = (перейдём к полярным координатам) =
= (перейдём к полярным координатам) =
 =
=
 =
=
 =
=
 =
=
 =
=
 .
.
Задание 3. Поверхностный интеграл первого рода.
Пусть в каждой точке поверхности S определена функция , которая может являться плотностью массы или электрического заряда распределённого по этой поверхности. Тогда масса всей поверхности или суммарный заряд определяются при помощи поверхностного интеграла первого рода
 .
.
Основными
свойствами этого интеграла являются
свойства: 1) линейность, то есть
 =
=
 +
+
 ,
где
,
где
 – постоянные; 2) аддитивност, то есть
=
– постоянные; 2) аддитивност, то есть
=
 +
+ ,
где
,
где
 ,
,
 –
части поверхности S,
которые могут пересекаться только по
линии и
–
части поверхности S,
которые могут пересекаться только по
линии и
 ;
3) если
;
3) если
 ,
тогда
,
тогда
 –площадь поверхности S.
–площадь поверхности S.
Вычисление поверхностного интеграла первого рода
Пусть поверхность
S задана в декартовых
координатах уравнением (либо
(либо
 или
или
 ),
тогда эта поверхность однозначно
проектируется на координатную плоскость
),
тогда эта поверхность однозначно
проектируется на координатную плоскость
 (на
координатные плоскости
(на
координатные плоскости
 или
или
 )
и эту проекцию будем обозначать
)
и эту проекцию будем обозначать
 .
Тогда поверхностный интеграл первого
рода вычисляется по такой формуле
.
Тогда поверхностный интеграл первого
рода вычисляется по такой формуле

Пример.
Вычислить
 ,
где поверхность S
является частью параболоида
,
где поверхность S
является частью параболоида
 .
.
В данном случае

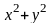 ,
,
 ,
проекцией
части
параболоида на плоскость
является круг
,
проекцией
части
параболоида на плоскость
является круг
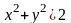 .
Следовательно,
=
.
Следовательно,
= = (перейдём к полярным координатам в
последнем интеграле) =
= (перейдём к полярным координатам в
последнем интеграле) =
= 4 =
=
 = (произведём замену пе –
= (произведём замену пе –
ременной
 )
=
)
=
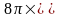
 =
=
 =
=
 =
=
 .
.
Если поверхность S проектируется на координатную плоскость не однозначно, тогда её разбивают на не пересекающие части, каждая из которых однозначно проектируется на координатную плоскость, а затем пользуются свойством аддитивности.
Пример.
Вычислить
 ,
где S – полная
поверхность сферы
,
где S – полная
поверхность сферы
 .
.
Сфера неоднозначно
проектируется на плоскость
,
поэтому разобьём её на две полусферы
 ,
уравнение которой
,
уравнение которой
 ,
и
,
и
 ,
уравнение которой
,
уравнение которой
 .
Проекцией полусфер
и
на
координатную плоскость
является круг
.
Проекцией полусфер
и
на
координатную плоскость
является круг ,
а
,
а
 =
=
 ,
,
 =
=
 для обеих полусфер
и
.
По свойству аддитивности поверхностного
интеграла первого рода получаем
для обеих полусфер
и
.
По свойству аддитивности поверхностного
интеграла первого рода получаем
=
 = 2
= 2 =
=
 (перейдём в интеграле к полярным
координатам) = 2
(перейдём в интеграле к полярным
координатам) = 2 =
=
 = (так как интеграл
= (так как интеграл
 )
=
)
=
 =
(произведём замену переменной
=
(произведём замену переменной

 ,
,

 )
=
)
=
 .
.
Поверхностный интеграл второго рода
Если в каждой
точке области V
пространства
 определена вектор
определена вектор
–
функция
,
тогда говорят, что в области V
задано векторное поле
 .
.
Пусть поверхность
S ,
тогда поверхностный интеграл
,
где
,
тогда поверхностный интеграл
,
где
 – единичный вектор нормали к поверхности
S в точке
– единичный вектор нормали к поверхности
S в точке
 ,
,
 – скалярное произведение векторов
и
,
называют потоком векторного поля
через поверхность S
в направлении нормали
.
Отметим, что поток в противоположном
направлении имеет противоположный знак
– скалярное произведение векторов
и
,
называют потоком векторного поля
через поверхность S
в направлении нормали
.
Отметим, что поток в противоположном
направлении имеет противоположный знак
 .
Поверхностный интеграл второго рода
можно вычислять двумя способами.
.
Поверхностный интеграл второго рода
можно вычислять двумя способами.
1). Если
поверхность S задана
уравнением
 ,
тогда вектор из частных производных
,
тогда вектор из частных производных
 ,
который называется градиентом функции
,
который называется градиентом функции
 ,
является нормалью к поверхности S
в точке
,
является нормалью к поверхности S
в точке
 (при этом
(при этом
 ).
Тогда вектор единичной нормали
).
Тогда вектор единичной нормали
 ,
а скалярное произведение
,
а скалярное произведение

 .
Подставив полученное выражение для
скалярного произведения в интеграл,
получим поверхностный интеграл первого
рода.
.
Подставив полученное выражение для
скалярного произведения в интеграл,
получим поверхностный интеграл первого
рода.
Пример.
Вычислить поток векторного поля
 через полную поверхность сферы
в направлении внешней нормали.
через полную поверхность сферы
в направлении внешней нормали.
Градиент
функции

 равен
равен
 =
=
 и является внешней нормалью к сфере.
Вектор единичной нормали
=
и является внешней нормалью к сфере.
Вектор единичной нормали
=
 .
Следовательно,
=
.
Следовательно,
=

 =
= .
.
Вычислим первый
интеграл. Как в предыдущем примере
разобьём сферу на две полусферы
и
,
уравнения которых
 соответственно,
а
соответственно,
а
 .
Имеем
.
Имеем
 =
=
 +
+
 = 2
= 2 ,
так как на
,
так как на
сфере
S будет
 ,
круг
–
проекция полусфер
и
на координатную плоскость
.
Переходя в последнем интеграле к
полярным координатам, получим 2
,
круг
–
проекция полусфер
и
на координатную плоскость
.
Переходя в последнем интеграле к
полярным координатам, получим 2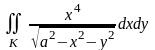 =
=
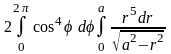 =
(произведём во внутреннем интеграле
замену
=
(произведём во внутреннем интеграле
замену

 ,
)
=
,
)
=
 =
=
 =
=
 ,
так как внутренний интеграл
,
так как внутренний интеграл
 =
=
 ,
а интеграл
,
а интеграл
 =
=
 .
.
Второй интеграл вычисляется аналогично и равен также .
Вычислим третий
интеграл:
 =
=
 +
+
 = 2
= 2 = (так как на
= (так как на
 ,
а
,
а
 =
=
 и
интегралы по
и
равны) =
и
интегралы по
и
равны) =
 = (переходим к полярным координатам) =
= (переходим к полярным координатам) =
 =
=
 .
Сложив полученные значения всех трёх
интегралов, получим, что искомый поток
равен
+
+
=
.
Сложив полученные значения всех трёх
интегралов, получим, что искомый поток
равен
+
+
= .
.
2). Пусть
поверхность S однозначно
проектируется на координатные плоскости
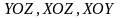 ,
вектор единичной нормали
,
вектор единичной нормали

 ,
где
,
где
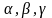 –
углы, которые вектор
образует с координатными осями OX,
OY, OZ
соответственно. Тогда
=
–
углы, которые вектор
образует с координатными осями OX,
OY, OZ
соответственно. Тогда
= +
+
 +
+
 =
=

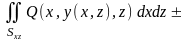
 ,
где знак + перед интегралом ставится в
том случае, если соответствующий угол
острый, а знак – ставится в том случае,
если соответствующий угол тупой (если
угол равен
,
где знак + перед интегралом ставится в
том случае, если соответствующий угол
острый, а знак – ставится в том случае,
если соответствующий угол тупой (если
угол равен
 ,
тогда косинус этого угла равен 0, а
значит, равен 0 и соответствующий
интеграл); функции
,
тогда косинус этого угла равен 0, а
значит, равен 0 и соответствующий
интеграл); функции
 ,
,
 находят из уравнения поверхности S.
Если поверхность S не
однозначно проектируется на какую либо
координатную плоскость, тогда её
разбивают на части, каждая из которых
однозначно проектируется на эту
плоскость, а затем используют свойство
аддитивности интеграла.
находят из уравнения поверхности S.
Если поверхность S не
однозначно проектируется на какую либо
координатную плоскость, тогда её
разбивают на части, каждая из которых
однозначно проектируется на эту
плоскость, а затем используют свойство
аддитивности интеграла.
Пример. Вычислить поток векторного поля через полную поверхность сферы в направлении внешней нормали.
Имеем,
= +
+ +
+
 .
Вычислим первый интеграл. Сфера S
не однозначно проектируется на плоскость
.
Вычислим первый интеграл. Сфера S
не однозначно проектируется на плоскость
 поэтому разобьём её на две полусферы
и
,
уравнения которых
поэтому разобьём её на две полусферы
и
,
уравнения которых
 .
Тогда, по свойству аддитивности интеграла,
=
.
Тогда, по свойству аддитивности интеграла,
=
 +
+
 =
=
 –
–
 = 2
= 2 ,
где круг
,
где круг



 –
проекция полусфер
и
на координатную плоскость
.
При этом интеграл по
берётся
со знаком +, а интеграл по
со знаком –, так как вектор нормали
на полусфере
образует
острый угол с осью OX, а на
полусфере
–
тупой угол. Перейдя в последнем интеграле
к полярным координатам:
–
проекция полусфер
и
на координатную плоскость
.
При этом интеграл по
берётся
со знаком +, а интеграл по
со знаком –, так как вектор нормали
на полусфере
образует
острый угол с осью OX, а на
полусфере
–
тупой угол. Перейдя в последнем интеграле
к полярным координатам:
 получим 2
=
=
получим 2
=
=
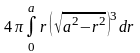 (сделаем замену
(сделаем замену


 )
=
)
=
 =
.
Следовательно,
=
.
Второй и третий интегралы вычисляются
также как первый и равны
.
Сложив все три интеграла, получим
=
.
=
.
Следовательно,
=
.
Второй и третий интегралы вычисляются
также как первый и равны
.
Сложив все три интеграла, получим
=
.
Задание 4. Формула Гаусса – Остроградского.
Определение. Дивергенцией (расходимостью) векторного поля в
точке
 называют предел отношения потока
векторного поля
через
замкнутую поверхность
называют предел отношения потока
векторного поля
через
замкнутую поверхность
 ,
окружающую точку M,
в направлении внешней нормали к объёму
тела
,
окружающую точку M,
в направлении внешней нормали к объёму
тела
 ,
ограниченного этой поверхностью, при
,
ограниченного этой поверхностью, при
 .
Дивергенция векторного поля
обозначается
.
Дивергенция векторного поля
обозначается
 и вычисляется по формуле:
и вычисляется по формуле:

 .
.
Векторное поле
называется соленоидальным, если
 .
.
Будем
предполагать, что функции
 и
их частные производные первого порядка
и
их частные производные первого порядка
 непрерывны.
непрерывны.
Пусть замкнутая
поверхность S является
границей ограниченной области
 пространства
.
Тогда поток векторного поля
через поверхность S
в направлении внешней нормали определяется
формулой Гаусса – Остроградского
пространства
.
Тогда поток векторного поля
через поверхность S
в направлении внешней нормали определяется
формулой Гаусса – Остроградского
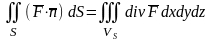 .
.
Из этой формулы следует, что в соленоидальном поле поток этого поля через замкнутую поверхность равен 0.
Пример. Вычислить, пользуясь формулой Гаусса – Остроградского, поток векторного поля через полную поверхность сферы в направлении внешней нормали.
Имеем
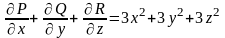 ,
а
=
,
а
=
 ,
где
–
шар
,
где
–
шар
 .
Для вычисления полученного интеграла
перейдём от декартовых координат к
сферическим координатам
.
Для вычисления полученного интеграла
перейдём от декартовых координат к
сферическим координатам
 :
:

где
r =
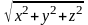 – расстояние от точки
– расстояние от точки
 до начала координат,
до начала координат,
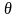 – угол, который радиус – вектор
точки
– угол, который радиус – вектор
точки
 образует
с осью OZ,
– угол, который радиус – вектор
образует
с осью OZ,
– угол, который радиус – вектор
 точки
точки
 (точка
является
проекцией точки
на плоскость XOY)
образует с осью OX. При
этом, определитель Якоби
(точка
является
проекцией точки
на плоскость XOY)
образует с осью OX. При
этом, определитель Якоби
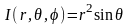 .
.
В сферических координатах получим =
3 =
=

Формула Стокса
Будем предполагать, что векторное поле дифференцируемо, то есть функции имеют непрерывные частные производные первого порядка.
Определение.
Вихрем векторного поля
,
обозначаемым
 называют вектор
называют вектор
 .
.
Теорема
Стокса. Циркуляция векторного поле
по кусочно гладкому замкнутому
контуру L равна потоку
поля
через
поверхность
 ,
ограниченную этим контуром:
,
ограниченную этим контуром:
 ,
,
или
в координатной форме
 =
=
 +
+
 +
+
 .
При этом вектор единичной нормали
к поверхности
должен быть направлен так, чтобы из
конца вектора
обход
контура L казался
осуществляемым против часовой стрелки
(в положительном направлении).
.
При этом вектор единичной нормали
к поверхности
должен быть направлен так, чтобы из
конца вектора
обход
контура L казался
осуществляемым против часовой стрелки
(в положительном направлении).
Пример.
Вычислить циркуляцию векторного поля
 по замкнутому контуру L,
образованному сечением сферы
плоскостью
по замкнутому контуру L,
образованному сечением сферы
плоскостью
 в положительном направлении относительно
орта
в положительном направлении относительно
орта
 .
.
Контур L
является окружностью радиуса a,
которая расположена в плоскости
,
а поверхностью
,
ограниченной этим замкнутым контуром,
является круг, ограниченный этой
окружностью. Вихрь векторного поля
 ,
вектор единичной нормали к поверхности
,
относительно которого контур L
обходится в положительном направлении,
,
вектор единичной нормали к поверхности
,
относительно которого контур L
обходится в положительном направлении,
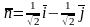 ,
скалярное произведение
,
скалярное произведение
 Следовательно, по теореме Стокса, искомая
циркуляция
Следовательно, по теореме Стокса, искомая
циркуляция
 =
=
 =
=
 (площадь
круга радиуса r) =
(площадь
круга радиуса r) =
 .
.
Задание 5.
Определение. Векторное поле
 называется потенциальным, если существует
функция
называется потенциальным, если существует
функция
 такая, что справед-
такая, что справед-
ливо
равенство
 или в скалярной форме
или в скалярной форме


 ,
а функция
называется потенциалом этого векторного
поля.
,
а функция
называется потенциалом этого векторного
поля.
Необходимым
и достаточным условием потенциальности
гладкого в односвязной области векторного
поля
является равенство нулю вихря этого
поля:

Потенциальные поля в области непрерывности потенциала обладают следующими важными свойствами.
Работа поля
не зависит от пути из точки A
в точку B и равна
разности значений потенциала в этих
точках, то есть, если
 –
два различных пути из точки A
в точку B, тогда
–
два различных пути из точки A
в точку B, тогда

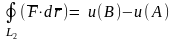 ;
;
Работа поля по любому замкнутому контуру равна нулю.
Пусть точка
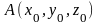 – фиксированная, а точка
– фиксированная, а точка
 –
произвольная точки области непрерывности
потенциального поля
.
Тогда потенциал этого поля можно
вычислить по следующей формуле:
–
произвольная точки области непрерывности
потенциального поля
.
Тогда потенциал этого поля можно
вычислить по следующей формуле:
 .
.
Пример. Убедиться в том, что векторное поле
=

потенциально и найти его потенциал.
Убедимся
сначала в том, что рассматриваемое поле
потенциально. Имеем, =
=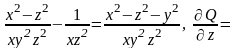

 Следовательно,
Следовательно,
 .
Аналогично,
.
Аналогично,
 .
Следовательно,
.
Следовательно,
 и поле
потенциально.
и поле
потенциально.
Выбрав
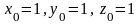 ,
находим потенциал
,
находим потенциал
 +
+
 +
+
 =
=
 +
+
 =
=
 =
=
 +
+ –
3. Следовательно, потенциал
–
3. Следовательно, потенциал
 +
+ .
.
Задание 6. Понятие числового ряда. Выражение вида
 или
или
 (3)
(3)
называют
числовым рядом. Числовую последовательность
 называют общим членом числового ряда
(3). Сумма первых n
членов числового ряда называется n
– той частичной суммой ряда и обозначается
называют общим членом числового ряда
(3). Сумма первых n
членов числового ряда называется n
– той частичной суммой ряда и обозначается
 .
Таким образом, возникает последовательность
частичных сумм ряда (3)
.
Таким образом, возникает последовательность
частичных сумм ряда (3)
 ,
,
 ,
,
 ,
,

Если существует
предел частичных сумм
 ,
тогда говорят, что ряд (3) сходится, а
число S называют суммой
этого ряда. Если же предел частичных
сумм не существует или равен ∞, тогда
говорят, что ряд (3) расходится.
,
тогда говорят, что ряд (3) сходится, а
число S называют суммой
этого ряда. Если же предел частичных
сумм не существует или равен ∞, тогда
говорят, что ряд (3) расходится.
Пример.
Рассмотрим числовой ряд
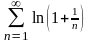 .
Преобразуем общий член этого ряда
.
Преобразуем общий член этого ряда
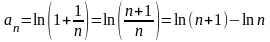 .
Тогда частичная сумма ряда
.
Тогда частичная сумма ряда
 =
=
 +
+
 +
+
+
+
 +
+
 =
=
 ,
так как все другие слагаемые сократились
в силу чередования знаков. Далее,
,
так как все другие слагаемые сократились
в силу чередования знаков. Далее,
 =
ln(n+1)
= ∞, а значит, рассматриваемый числовой
ряд расходится.
=
ln(n+1)
= ∞, а значит, рассматриваемый числовой
ряд расходится.
Пример.
Исследуем сходимость ряда
 .Общий
член этого ряда можно представить в
виде разности
.Общий
член этого ряда можно представить в
виде разности
 ,
следовательно,
=
,
следовательно,
=
 +
+
 +
+
 +
+

+
 = 1–
= 1–
 .
Таким образом,
=
.
Таким образом,
=
 = 1 и рассматриваемый ряд сходится, а его
сумма равна 1.
= 1 и рассматриваемый ряд сходится, а его
сумма равна 1.
Необходимый признак сходимости числового ряда
Если числовой
ряд (3) сходится, тогда

Действительно,
из сходимости ряда (3) следует существование
 .
Тогда
.
Тогда
 =
=


 =
=
 =
0.
=
0.
Из необходимого
признака сходимости ряда следует
достаточный признак расходимости
ряда: если
 ,
тогда ряд
расходится.
,
тогда ряд
расходится.
Пример.
Числовой ряд
 расходится так как
=
расходится так как
=
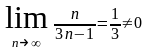 .
.
Свойства числовых рядов
Числовые ряды обладают следующими свойствами:
1) если ряд
 получен из ряда (3) отбрасыванием конечного
числа слагаемых, тогда эти ряды сходятся
или расходятся одновременно;
получен из ряда (3) отбрасыванием конечного
числа слагаемых, тогда эти ряды сходятся
или расходятся одновременно;
2) ряды
и
 ,
где
,
где
 ,
сходятся или расходятся одновременно
и справедливо равенство
,
сходятся или расходятся одновременно
и справедливо равенство
 ;
;
3) если ряды
и
 сходятся,
тогда сходятся ряды
сходятся,
тогда сходятся ряды
 и справедливы равенства
=
и справедливы равенства
=
 .
.
Проиллюстрируем
свойство 1) –3) на следующем примере.
Известно, что ряд
 сходится,
если
сходится,
если
 ,
и его сумма равна
,
и его сумма равна
 Следовательно, числовой ряд
Следовательно, числовой ряд
 сходится и справедливо равенство
=
сходится и справедливо равенство
=

 =
=
 +
+
 =
=
 +
+
 =
=
 =
= .
.
Признаки сходимости положительных рядов
Ряды (3), у
которых все члены являются положительными
числами,
 ,
называются положительными рядами.
Вначале рассмотрим признаки сравнения
положительных рядов.
,
называются положительными рядами.
Вначале рассмотрим признаки сравнения
положительных рядов.
1. Мажорантный признак сравнения.
Пусть даны два положительных ряда
(1) , (2) .
Если для любых
 (начиная
с номера
(начиная
с номера
 )
выполняется неравенство
)
выполняется неравенство
 ,
,
тогда из сходимости ряда (2) (большего ряда) следует сходимость ряда (1) (меньшего ряда), а из расходимости ряда (1) следует расходимость ряда (2).
Пример. Ранее
было доказано, что ряд
расходится. Докажем расходимость
гармонического ряда
 .
Воспользуемся неравенством
.
Воспользуемся неравенством
 для любых
для любых
 .
Действительно, рассмотрим функцию
.
Действительно, рассмотрим функцию
 .
Так как производная
.
Так как производная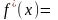
 =
=
 для всех
,
то функция
монотонно возрастает на промежутке
для всех
,
то функция
монотонно возрастает на промежутке
 ,
а значит, для любых
выполняется неравенство
,
а значит, для любых
выполняется неравенство

 .
Так как
.
Так как
 ,
то выполнено неравенство
,
то выполнено неравенство
 и, гармонический ряд расходится.
и, гармонический ряд расходится.
