
- •Часть 2
- •Часть 2
- •Задания к контрольной работе 3
- •Методические указания к контрольной работе 3
- •2. Предельный признак сравнения.
- •5. Интегральный признак Коши.
- •1) , 2) (Последовательность убывает), тогда знакочередующийся ряд (4) сходится.
- •Однородное уравнение.
- •Линейным уравнением первого порядка называется уравнение вида , (11)
- •5. Уравнением Бернулли называют уравнение следующего вида
- •Уравнение со специальной правой частью второго типа.
- •Метод вариации произвольных постоянных.
- •Задания к контрольной работе 4
- •Методические указания к контрольной работе 4
- •Число размещений .
- •Число перестановок .
- •Число сочетаний .
- •Формула полной вероятности.
- •Формула Байеса.
Однородное уравнение.
Определение. Функция называется однородной нулевой
степени,
если для любого числа
 выполняется равенство
выполняется равенство
 =
.
Дифференциальное уравнение вида
=
.
Дифференциальное уравнение вида
 называется однородным, если функция
однородна нулевой степени.
называется однородным, если функция
однородна нулевой степени.
Так
как в однородном уравнении функция
является однородной нулевой степени,
то
=
 =
= =
=
 и однородное уравнение всегда можно
привести к виду
и однородное уравнение всегда можно
привести к виду
 .
(10)
.
(10)
Уравнение (10)
заменой
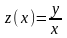 или
или
 приводится к уравнению с разделяющимися
переменными. Действительно, из формулы
замены
приводится к уравнению с разделяющимися
переменными. Действительно, из формулы
замены
получаем
 ,
а уравнение (10) примет вид
,
а уравнение (10) примет вид
 или
или
 – уравнение с разделяющимися переменными.
Найдя общее решение
– уравнение с разделяющимися переменными.
Найдя общее решение
 полученного уравнения с разделяющимися
переменными, из формулы замены найдём
общее решение однородного уравнения
(10)
полученного уравнения с разделяющимися
переменными, из формулы замены найдём
общее решение однородного уравнения
(10)
 .
.
Пример. Найдём
общее решение уравнения
 .
.
После
преобразования правой части данного
уравнения
=
 =
=
 видно, что данное уравнение
видно, что данное уравнение
 является однородным. После замены
,
получим уравнение с разделяющимися
переменными
является однородным. После замены
,
получим уравнение с разделяющимися
переменными
 или
или
 .
Разделим переменные:
.
Разделим переменные:
 ,
,
 ,
,
 .
Интегрируя последнее равенство, получим
.
Интегрируя последнее равенство, получим
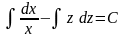 или
или
 .
Разрешим последнее равенство относительно
.
Разрешим последнее равенство относительно
 :
:
 ,
,
 =
=
 ,
,
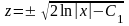 .
Из формулы замены получаем теперь общее
решение исходного уравнения
.
Из формулы замены получаем теперь общее
решение исходного уравнения

 .
.
Линейным уравнением первого порядка называется уравнение вида , (11)
где
 –
заданные функции.
–
заданные функции.
Линейное
уравнение (11) приводится к уравнению
вида
 следующей заменой
следующей заменой
 ,
где
,
где
 является
новой искомой функцией.
является
новой искомой функцией.
Пример.
Решить задачу Коши для уравнения
 с начальным условием
с начальным условием
 .
.
Произведём
в данном уравнении замену
 =
= .
Для новой искомой функции
получим уравнение
.
Для новой искомой функции
получим уравнение
 –
–
 +
=
+
=
 .
После сокращения второго и третьего
слагаемых в левой части последнего
равенства, получим уравнение
.
После сокращения второго и третьего
слагаемых в левой части последнего
равенства, получим уравнение
 или
или
 .
Следовательно,
.
Следовательно,
 =
=
 ,
то есть общее решение данного уравнения
,
то есть общее решение данного уравнения
 =
=
 .
Для того, чтобы найти решение задачи
Коши, подставим в общее решение
.
Для того, чтобы найти решение задачи
Коши, подставим в общее решение
 и
получим 1= 1 + C,
и
получим 1= 1 + C,
 .
Из общего решения с
получаем решение задачи Коши
.
Из общего решения с
получаем решение задачи Коши
 .
.
5. Уравнением Бернулли называют уравнение следующего вида
 ,
,
 (12)
(12)
Уравнение (11) заменой , приводится к уравнению с разделяющимися переменными.
Пример. Найти
общее решение уравнения
 .
.
Это
уравнение является уравнением Бернулли.
Произведя в этом уравнении замену
 =
= ,
,
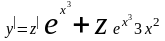 ,
получим уравнение
,
получим уравнение

 или
или
 =
=
 ,
,
 =
=
 –
уравнение с разделяющимися переменными.
Разделим переменные:
–
уравнение с разделяющимися переменными.
Разделим переменные:
 ,
,
 ,
,
 .
Интегрируя последнее равенство, получаем
.
Интегрируя последнее равенство, получаем
 ,
,
 ,
,

 ,
,
 .
Из формулы замены находим теперь, что
.
Из формулы замены находим теперь, что
 =
=
 +
+ –
общее решение данного уравнения.
–
общее решение данного уравнения.
Линейные дифференциальные уравнения более высокого порядка
Уравнение вида
 ,
(13)
,
(13)
где
 –
данные действительные числа,
–
данная функция, называют линейным
дифференциальным уравнением порядка
с постоянными коэффициентами. Если в
уравнении (13)
–
данные действительные числа,
–
данная функция, называют линейным
дифференциальным уравнением порядка
с постоянными коэффициентами. Если в
уравнении (13)
 ,
тогда это уравнение называется однородным
и имеет вид
,
тогда это уравнение называется однородным
и имеет вид
 .
(14)
.
(14)
Рассмотрим
функцию
 .
Подставив эту функцию в уравнение (14),
получим равенство
.
Подставив эту функцию в уравнение (14),
получим равенство
 ,
из которого видно, что функцию
является решением однородного уравнения
(14) тогда и только тогда когда число
,
из которого видно, что функцию
является решением однородного уравнения
(14) тогда и только тогда когда число
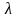 является решением алгебраического
уравнения
является решением алгебраического
уравнения
 .
(15)
.
(15)
Уравнение (15) называется характеристическим уравнением, соответствующим уравнениям (13), (14).
Определение. Система линейно независимых решений однородного уравнения (14) называется фундаментальной системой решений этого уравнения. Отметим, что такая система всегда существует и общие решения уравнений (13), (14) определяются фундаментальной системой решений.
Теорема.
Пусть функции
 образуют фундаментальную систему
решений уравнения (14). Тогда: 1) функция
образуют фундаментальную систему
решений уравнения (14). Тогда: 1) функция
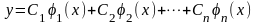 ,
где
,
где
 –
произвольные постоянные, является общим
решением однородного уравнения (14); 2)
функция
–
произвольные постоянные, является общим
решением однородного уравнения (14); 2)
функция
 ,
где
,
где
 –
частное решение неоднородного уравнения
(13), является общим решением уравнения
(13).
–
частное решение неоднородного уравнения
(13), является общим решением уравнения
(13).
Для
построения фундаментальной системы
решений сначала находятся все корни
характеристического уравнения, которые
могут быть двух типов: 1) действительные
корни кратности
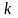 (
=1,2,…);
2) комплексные корни кратности
(
=1,2,…).
Если
действительный корень характеристического
уравнения кратности
,
тогда
функций
(
=1,2,…);
2) комплексные корни кратности
(
=1,2,…).
Если
действительный корень характеристического
уравнения кратности
,
тогда
функций
 включаются в фундаментальную систему.
Если комплексное число
включаются в фундаментальную систему.
Если комплексное число
 является корнем кратности
характеристического
уравнения, тогда и комплексно сопряжённое
к нему число
является корнем кратности
характеристического
уравнения, тогда и комплексно сопряжённое
к нему число
 также будет корнем характеристического
уравнения кратности
(это
следует из того, что коэффициенты
уравнения (15) являются действительными
числами). Этой паре комплексно сопряжённых
корней соответствует 2
действительных
решений однородного уравнения (14) вида
также будет корнем характеристического
уравнения кратности
(это
следует из того, что коэффициенты
уравнения (15) являются действительными
числами). Этой паре комплексно сопряжённых
корней соответствует 2
действительных
решений однородного уравнения (14) вида
 ,
,
 ,
которые также включаются в фундаментальную
систему решений. Так как полином степени
имеет
ровно n
комплексных корней с учётом кратности,
то построенная фундаментальная система
будет содержать ровно n
линейно независимых решений однородного
уравнения (14).
,
которые также включаются в фундаментальную
систему решений. Так как полином степени
имеет
ровно n
комплексных корней с учётом кратности,
то построенная фундаментальная система
будет содержать ровно n
линейно независимых решений однородного
уравнения (14).
Рассмотрим теперь более подробно случай уравнений второго порядка, которые чаще встречаются в приложениях. Уравнения (13),(14) в этом случае имеют вид
 ,
,
 ,
(16)
,
(16)
а характеристическое уравнение является квадратным уравнением
 .
Возможны три случая.
.
Возможны три случая.
Характеристическое уравнение имеет два различных
действительных
корня
 ,
то есть дискриминант этого уравнения
,
то есть дискриминант этого уравнения
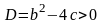 .
В этом случае функции
.
В этом случае функции
 образуют фундаментальную систему
решений, а функция
образуют фундаментальную систему
решений, а функция
 является общим решением однородного
уравнения (16).
является общим решением однородного
уравнения (16).
Пример.
Найдём общее решение уравнения

Данному
уравнению соответствует характеристическое
уравнение
 ,
которое имеет два различных действительных
корня
,
которое имеет два различных действительных
корня
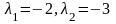 .
Следовательно,
.
Следовательно,
 –
общее решение.
–
общее решение.
Характеристическое уравнение имеет один действительный корень
кратности 2, то есть дискриминант этого
уравнения
 .
В этом случае функции
.
В этом случае функции
 образуют фундаментальную систему
решений, а функция
образуют фундаментальную систему
решений, а функция
 является общим решением однородного
уравнения (16).
является общим решением однородного
уравнения (16).
Пример.
Найдём общее решение уравнения

Данному
уравнению соответствует характеристическое
уравнение
 ,
которое имеет корень
,
которое имеет корень
 кратности 2. Следовательно,
кратности 2. Следовательно,
 –
общее решение.
–
общее решение.
Характеристическое уравнение имеет пару комплексно сопряжённых
корней
 ,
то есть дискриминант этого уравнения
,
то есть дискриминант этого уравнения
 .
В этом случае действительные функции
образуют фундаментальную систему
решений, а функция
.
В этом случае действительные функции
образуют фундаментальную систему
решений, а функция
 является общим решением однородного
уравнения (16).
является общим решением однородного
уравнения (16).
Пример.
Найдём общее решение уравнения

Данному
уравнению соответствует характеристическое
уравнение
 ,
которое имеет два комплексно сопряжённых
корня
,
которое имеет два комплексно сопряжённых
корня
 .
Следовательно,
.
Следовательно,
 –
общее решение.
–
общее решение.
Отыскание общего решения неоднородного уравнения
Уравнение со специальной правой частью первого типа.
Теорема.
Пусть функция
в правой части неоднородного уравнения
(13) имеет вид
 ,
где
,
где
 –
полином степени n.
–
полином степени n.
Тогда уравнение (13) имеет частное решение
вида
 ,
где
,
где
 –
полином степени n с
неопределёнными коэффициентами (эти
коэффициенты находят подстановкой
функции
в уравнение (13)), k–
кратность числа a как
корня характеристического уравнения
(если a не является
корнем этого уравнения, то k
= 0).
–
полином степени n с
неопределёнными коэффициентами (эти
коэффициенты находят подстановкой
функции
в уравнение (13)), k–
кратность числа a как
корня характеристического уравнения
(если a не является
корнем этого уравнения, то k
= 0).
Пример.
Найдём общее решение неоднородного
уравнения второго порядка
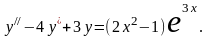
Это
уравнение со специальной правой частью,
которая содержит полином второй степени
 и a = 3. Характеристическое
уравнение
и a = 3. Характеристическое
уравнение
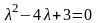 имеет два действительных корня
имеет два действительных корня
 .
Следовательно,
.
Следовательно,
 –
общее решение однородного уравнения,
а частное решение неоднородного уравнения
нужно искать в следующем виде
–
общее решение однородного уравнения,
а частное решение неоднородного уравнения
нужно искать в следующем виде
 =
=
 (в рассматриваемом случае k
= 1, так как число a = 3
является корнем характеристического
уравнения кратности 1). Вычислим
производные
(в рассматриваемом случае k
= 1, так как число a = 3
является корнем характеристического
уравнения кратности 1). Вычислим
производные
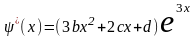 +
+
 ,
,
 +
+
 +
+
+
+
 .
Заменив в данном уравнении
.
Заменив в данном уравнении
 функциями
функциями
 и сократив на
и сократив на
 ,
получим равенство двух полиномов
,
получим равенство двух полиномов
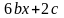 +
+
 +
+
+
+
 –
–
 –
–
 +
+ =
.
Приведя в последнем равенстве подобные
члены, получим
=
.
Приведя в последнем равенстве подобные
члены, получим
 .
Для определения коэффициентов
.
Для определения коэффициентов
 приравниваем коэффициенты при одинаковых
степенях x, и получаем
систему трёх линейных уравнений с тремя
неизвестными
приравниваем коэффициенты при одинаковых
степенях x, и получаем
систему трёх линейных уравнений с тремя
неизвестными

из
которой находим
 .
Следовательно, частное решение
неоднородного уравнения
.
Следовательно, частное решение
неоднородного уравнения
 ,
а общее решение рассматриваемого
уравнения
,
а общее решение рассматриваемого
уравнения
 .
.
Пример.
Найдём общее решение уравнения

Характеристическое
уравнение
 имеет действительный корень
имеет действительный корень
 кратности 2. Следовательно,
кратности 2. Следовательно,
 –
общее ре–
–
общее ре–
шение
однородного уравнения, а частное решение
неоднородного уравнения нужно искать
в виде
 (в этом случае k = 2, так
как число a = 2 является
корнем характеристического уравнения
кратности 2). Имеем
(в этом случае k = 2, так
как число a = 2 является
корнем характеристического уравнения
кратности 2). Имеем
 ,
,
 .
Подставив
в уравнение, и сократив на
.
Подставив
в уравнение, и сократив на
 ,
получим равенство
,
получим равенство
 –
–
 или, после привидения подобных членов,
2A = 1,
или, после привидения подобных членов,
2A = 1,
 .
Следовательно, частное решение
неоднородного уравнения
.
Следовательно, частное решение
неоднородного уравнения
 ,
а общее решение рассматриваемого
неоднородного уравнения
,
а общее решение рассматриваемого
неоднородного уравнения
 .
.
