2. Предельный признак сравнения.
Пусть для общих
членов рядов (1), (2) существует конечный
предел
,
тогда эти ряды сходятся или расходятся
одновременно.
Для успешного
использования признаков сравнения
необходимо иметь в своём распоряжении
набор числовых рядов, о которых известно
сходятся они или расходятся. Поэтому к
уже рассмотренным рядам добавим
обобщённые гармонические ряды
,
которые сходятся, если
и расходятся, если
.
Пример.
Исследуем сходимость ряда
.
Сначала
установим
асимптотику общего члена ряда при
,
отбросив в числителе и знаменателе
дроби меньшие степени
.
Так как последовательность
эквивалентна
,
если
,
то исследуемый ряд необходимо сравнивать
с обобщённым гармоническим рядом
.
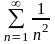Имеем,
=
=
.
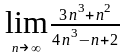Следовательно, рассматриваемый ряд
сходится, как и ряд
.
Пример. Ряд
сходится, если
и расходится, если
.
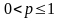Так как в этом случае
то, по первому замечательному пределу
,
будет выполнено равенство
и ряды
и
сходятся или расходятся одновременно.
Аналогично из
равенств
,
,
следует, что ряды
,
,
сходятся, если
и расходятся, если
.
3. Признак Даламбера.
Пусть
общий член ряда (3) и существует
(может быть k = +∞).
Тогда: 1) если
,
то ряд (3) сходится; 2) если
,
то ряд (3) расходится; 3) если
,
то признак Даламбера не даёт ответ о
сходимости ряда и необходимо применять
другие признаки.
Заметим, что
признак Даламбера следует применять
тогда, когда общий член ряда содержит
сомножители вида n!,
.
Пример.
Исследуем сходимость ряда
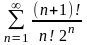с помощью признака Даламбера. Имеем,
,
(
получается из
заменой
на
),
=
=
.
Следовательно,
и исследуемый ряд сходится.
4. Радикальный признак Коши.
Пусть
общий член ряда (3) и существует
(может быть k = +∞).
Тогда: 1) если
,
то ряд (3) сходится; 2) если
,
то ряд (3) расходится; 3) если
,
то признак Коши не даёт ответ о сходимости
ряда и необходимо применять другие
признаки.
Отметим, что
для практического применения этого
признака необходимо знать следующие
пределы: 1)
,
где p > 0; 2)
;
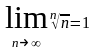3)
,
где p – любое постоянное
число, так как
=
=
при
;
4)
,
где
,
–
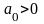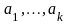постоянные числа.
Пример.
Исследуем сходимость ряда
.
По признаку Коши
=
<
1 и рассматриваемый ряд сходится.
Пример. Ряд
расходится
так как, по признаку Коши,
>
1.
Отметим, что
если учесть очевидное неравенство
,
которое выполняется для любых
,
получим неравенство
.
А так как 1 и
,
если
,
то, по достаточному признаку существования
предела, существует
1.
Из последнего равенства следует, что
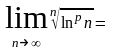1
для любого постоянного числа p.
Поэтому с
помощью радикального признака Коши
можно исследовать сходимость рядов
вида
,
которые сходятся, если a
> 1, и расходятся, если a
< 1, так как
,
если
.
5. Интегральный признак Коши.
Если общий
член ряда (3) убывает, то есть
для любых
,
функция f(x)
убывает на промежутке
и
.
Тогда несобственный интеграл
и ряд
сходятся
или расходятся одновременно.
Пример. Чтобы
исследовать сходимость ряда
,
где постоянная p >
0, рассмотрим несобственный интеграл
.
После замены переменной
в этом интеграле получаем
=
=
(
)
=
=
–
=
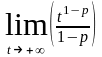так как
,
если
,
и
,
если
.
В случае
имеем
.
Следовательно, несобственный интеграл, а значит и рассматриваемый ряд, сходятся, если , и расходятся, если .
Пример.
Исследуем сходимость ряда
.
Докажем сначала,
что последовательность
убывает. Для этого рассмотрим функцию
.
Имеем,
=
<
0, если будет выполнено неравенство
или
,
или
.
Следовательно, функция
монотонно убывает для x
> 2, а значит, убывает и последовательность
.
Для вычисления несобственного интеграла
применим формулу интегрирования по
частям:
=
=
+
= (так как
)
=
=
(так как
).
Следовательно, несобственный интеграл
сходится, а значит, сходится и
рассматриваемый ряд.
Знакопеременные ряды
Числовой ряд (3) называется знакопеременным, если у него существуют как положительные, так и отрицательные слагаемые со сколь угодно большими номерами.
Кроме знакопеременного ряда (3) будем рассматривать положительный ряд из абсолютных величин:
(3),
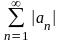(4).
Говорят, что знакопеременный ряд (3) сходится абсолютно, если сходится ряд из абсолютных величин (4); если же ряд (4) расходится, а сам ряд (3) сходится, то говорят, что знакопеременный ряд (3) сходится не абсолютно или условно.
Отметим, что из сходимости ряда (4) следует сходимость ряда (3), то есть из абсолютной сходимости знакопеременного ряда следует его сходимость. Абсолютно и условно сходящиеся ряды сильно отличаются по своим свойствам: 1) сумма абсолютно сходящегося ряда не меняется при любой перестановке его членов, 2) для любого действительного числа S можно так переставить местами члены условно сходящегося ряда, что сумма нового ряда будет равна S. По этой причине важно уметь различать абсолютно и условно сходящиеся ряды.
Пример. Ряд
является знакопеременным рядом, так
как
принимает как отрицательные, так и
положительные значения. Ряд из абсолютных
величин
сходится, так как справедливо неравенство
.
Ряд
сходится. Следовательно, по мажорантному
признаку сравнения, сходится ряд из
абсолютных величин, а значит, рассматриваемый
знакопеременный ряд сходится абсолютно.
Важным частным случаем знакопеременных рядов являются знакочередующиеся ряды вида
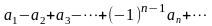или
,
(4)
где для всех значений .
Для исследования сходимости таких рядов используют признак Лейбница: если общий член ряда (4) удовлетворяет условиям: