
- •3.1. Общие приёмы решения уравнений
- •3.1.2. Разложение выражений на множители
- •3.1.3. Замена переменных в уравнении
- •3.1.4. Линейные уравнения
- •3.1.5. Квадратные уравнения
- •3.1.6. Алгебраические уравнения
- •3.1.7. О понятии одз
- •1.1.8. Уравнения, содержащие модуль
- •3.1.9. Показательные и логарифмические уравнения
- •3.1.10. Тригонометрические уравнения
3.1.7. О понятии одз
ОДЗ (областью допустимых значений) уравнения называется множество тех значений неизвестной, при которых определены его правая и левая части.
Очевидно, что вне ОДЗ решений не существует, однако не все числа, входящие в ОДЗ, служат решениями уравнения.
Уравнение можно решить и не находя ОДЗ. С другой стороны, верно найденное ОДЗ и последующий отбор корней с его помощью не может гарантировать отсутствие ошибок.
Приведём два примера, принадлежащих И. Ф. Шарыгину, показывающих, что нахождение ОДЗ может быть как чрезвычайно сложной с одной стороны, так и абсолютно необходимой, с другой стороны, задачей.
Пример 1
Решите
уравнение
![]()
Решение
Совершенно понятно, что поиск ОДЗ в данном примере сопряжён с огромными трудностями. Однако попробуем решить это уравнение непосредственно. Поскольку мы будем лишь возводить в квадрат, то ОДЗ может лишь расшириться, то есть могут появиться посторонние корни. Однако эти корни мы можем отсеять проверкой. Имеем:
Проверкой убеждаемся, что из двух найденных корней подходит только 1. Так как при возведении в квадрат мы не могли потерять решения, а могли только их приобрести, то 1 и есть окончательный ответ. Ответ. 1. |
Пример 2
Решите
уравнение
![]()
Решение
В этом примере наоборот сложно его решение. Однако поиск ОДЗ приносит несомненную пользу. В самом деле, ОДЗ:
Значит, ОДЗ нашего уравнения содержит только два числа. А поскольку вне ОДЗ решений быть не может, то корнями нашего уравнения могут быть только эти два числа. Для того чтобы понять, какое из них действительно является решением, нужно полученные числа подставить в уравнение. Подстановка даёт, что x = 0 не является решением уравнения, а x = 1 − является. Ответ. 1. |
Таким образом, к понятию ОДЗ нужно относиться творчески и искать его, только если в этом возникает существенная необходимость. Так, например, в равносильном переходе
|
требование g (x) ≥ 0 задаёт ОДЗ. Однако, если искать g (x) очень сложно, то проще подставить найденные корни в исходное уравнение, чем выяснять, при каких x выполнено неравенство g (x) ≥ 0.
1.1.8. Уравнения, содержащие модуль
Самый распространённый, а иногда и единственно возможный метод решения уравнений с модулем – раскрытие модуля согласно определению:
|
Пример 1
Решите уравнение |x – 5| – |2x + 8| = –12.
Решение
Выражения, стоящие под знаком абсолютной величины, обращаются в нуль при x = –4 и x = 5. Значит, нужно рассмотреть 3 случая: 1) x ≤ –4; 2) –4 < x ≤ 5; 3) x > 5. Получим три уравнения, в каждом из которых на неизвестное наложено ограничение. На рисунке схематично показано, какой знак будут иметь подмодульные выражения на каждом из трёх промежутков.
x = –25 удовлетворяет ограничению x ≤ –4.
Ответ. −25; 3. |
Этот метод удобно применять, когда подмодульные выражения довольно просты (линейны), и можно сразу понять, где они обращаются в нуль. Рассмотрим простейшее уравнение с модулем вида
|
|f (x)| = g (x), |
(9) |
где функция f (x) проще функции g (x). Это уравнение равносильно следующей системе уравнений:
|
Убедиться в справедливости этого утверждения можно, перебрав все возможные варианты.
Если же под модулем стоит функция, найти корни которой затруднительно, то условие равносильности можно переписать так:
|
Пример 2
Решите уравнение 2|x2 + 2x – 5| = x – 1.
Решение
Этому уравнению соответствуют два уравнения 2(x2 + 2x – 5) = x – 1 и 2(x2 + 2x – 5) = 1 – x, среди корней которых нужно отобрать удовлетворяющие условию x ≥ 1. Имеем: 1.
2.
Ответ. |
В случае вложенных знаков модуля применим этот метод несколько раз. Здесь тоже можно рассмотреть весь набор получающихся при раскрытии модуля уравнений среди решений которых содержатся решения исходного уравнения, а потом отобрать из всех полученных решений подходящие хотя бы с помощью проверки.
Пример 3
Решите
уравнение
![]()
Решение
Все корни исходного уравнения содержатся среди корней двух уравнений
которые можно переписать в виде
Аналогично, каждое из этих уравнений распадается на два:
что приводит к четырём уравнениям:
Отсюда
получаем 4 решения:
Ответ. 3. |



 С
учётом этого уравнение принимает вид
С
учётом этого уравнение принимает вид


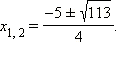 Опять
подходит только первый корень, так
как второй заведомо отрицателен.
Опять
подходит только первый корень, так
как второй заведомо отрицателен.




