2. Вычисление статических моментов и координат центров тяжести плоских фигур.
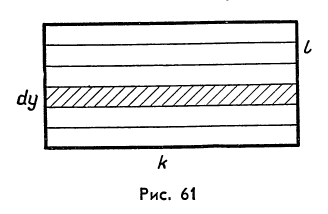
Найдем статический момент прямоугольника со сторонами k и l относительно стороны k. Разобьем этот прямоугольник на элементарные прямоугольники, имеющие стороны k и dy (рис. 61). Масса элементарного прямоугольника равна его площади kdy (напоминаем, что по предложению плотность распределения массы равна единице). Поэтому элементарный статический момент равен ky dy, а статический момент всего прямоугольника равен:
=
=
.
(1)
Теперь уже легко найти статический момент криволинейной трапеции, ограниченной сверху кривой = , где - непрерывная и неотрицательная функция на отрезке [a;b], снизу осью абсцисс, а с боков прямыми x=a, x=b.
Разобьем
криволинейную трапецию на элементарные
прямоугольники, основание каждого из
которых равно dx
и высота y.
Статический момент такого прямоугольника
относительно оси абсцисс по формуле
(1) равен 
.
В случае когда не выполняется предположение
о не отрицательности функции y=
,
эту формулу надо заменить такой:
=
- (части фигуры, расположенные ниже оси
абсцисс, дают отрицательный вклад в
).
Поскольку
по предположению плотность равна
единице, то масса криволинейной трапеции
равна ее площади, т.е. интегралу 
,
а потому ордината центра тяжести этой
трапеции выражается формулой:
=
.
Нетрудно найти и статический момент криволинейной трапеции относительно оси ординат. Для этого достаточно заметить, что расстояние элементарного прямоугольника от этой оси равно x. Поэтому его статический момент равен x|y|dx, а статический момент всей трапеции выражается формулой:
=
.
Следовательно, абсцисса центра тяжести выражается так:
=
.
Пример
3.
Найдем статический момент (относительно
оси Ox)
фигуры, ограниченной осью абсцисс и
одной аркой циклоиды: x=
-
,
y=
-
.
Решение. Так как параметр t одной арки циклоиды изменяется от 0 до 2 , то:
=
-
-
=
-
=
-3
+
+
-(
-
))|
=
+
=
.
Пример
4.
Найдем центр тяжести фигуры, ограниченной
осью Ox
и одной полуволной синусоиды y=
.
Решение.
Так как фигура под полуволной синусоиды
расположена симметрично относительно
прямой x=
,
то центр тяжести лежит на этой прямой
и, следовательно,
=
.
Ордината
центра тяжести находится по формуле:
=
.
Так как:
=
=-
=2,
то
=
=
.
Итак,
центр тяжести данной фигуры находится
в точке (
.
Пример 5. Найдем центр тяжести фигуры, ограниченной осью абсцисс и одной циклоиды x= - , y= - .
Решение.
Данная фигура расположена симметрично
относительно прямой x=
,
следовательно, центр тяжести ее находится
на этой прямой, и потому
=
.
Найдем
по формуле:
=
.
Площадь
S
данной фигуры была вычислена раньше,
она равна 3
.
Следовательно,
=
-
=
.
Центр
тяжести данной фигуры находится в точке
(
.
3. Теорема Гульдина-Паппа.
Выведем теоремы, связывающие площадь поверхности (соответственно, объем тела) вращения с центром тяжести вращающейся дуги (соответственно, криволинейной трапеции).
Пусть поверхность образована вращением дуги Г, имеющей длину l. Мы знаем, что ордината центра тяжести этой дуги выражается формулой:
=
.
Так как площадь поверхности вращения выражается интегралом:
=2
,
из этого следует, что:
=2
.
Мы доказали следующее утверждение, называемое первой теорией Гульдина-Паппа.
Площадь поверхности, полученной от вращения кривой вокруг непересекающей ее оси, равна произведению длины l дуги этой кривой на длину окружности, описанной центром тяжести C этой кривой.
Аналогично, из формулы, выражающей ординату центра тяжести криволинейной трапеции:
=
и формулы объема тела вращения: 
=
-
получаем
=
,
т.е. следующее утверждение, называемое
второй теоремой Гульдина-Паппа:
Объем тела, полученного от вращения плоской фигуры вокруг непересекающей ее оси, равен произведению площади этой фигуры на длину окружности, описанной центром тяжести этой фигуры.
Пользуясь этими двумя теоремами, можно в ряде случаев упростить процесс вычисления поверхности или объема тела вращения.
Пример
6.
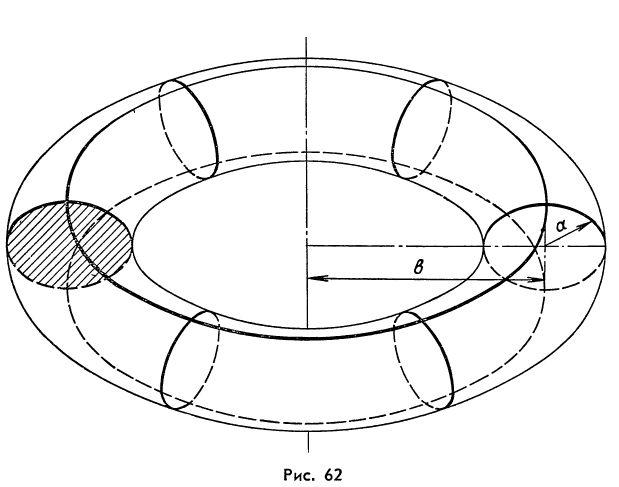
Пользуясь теоремой Гульдина-Паппа,
вычислим площадь поверхности и объема
тора (рис. 62), образованного вращением
круга радиуса a
вокруг оси, расположенной в его плоскости
и отстоящей от центра его на расстоянии
b
(a
b).
Решение.
Так как длина данной окружности равна
2
,
а длина окружности, описанной центром
тяжести ее, равна 2
,
то поверхность тора по первой теореме
Гульдина-Паппа равна:
=
=
.
Объем
тора равен:
=
=
.
Пример
7.
Длина одной арки циклоиды 
=
-
),
=
-
равна 
,
а площадь поверхности, образованной
вращением ее вокруг оси Ox,
равна 
.
Вычислим площадь поверхности, образованной
вращением той же арки циклоиды вокруг
касательной в верхней ее точке (рис.
63).
Решение.
Пусть
- расстояние центра тяжести дуги от оси
Ox,
тогда
по первой теореме Гульдина-Паппа:
=
,
откуда:
=
.
наибольшая
ордината кривой соответствует 
=
и равна 2
,
причем касательная в этой точке
параллельна оси Ox;
следовательно, расстояние h
центра тяжести этой касательной равно:
-
=
.
Таким
образом, площадь поверхности, образованной
вращением той же арки циклоиды вокруг
касательной в верхней ее точке, равна:
=
=
.
Пример 8. Найдем объем тела, полученного от вращения квадрата со стороной a вокруг оси Ox, если он расположен так, как показано на рисунке 64.
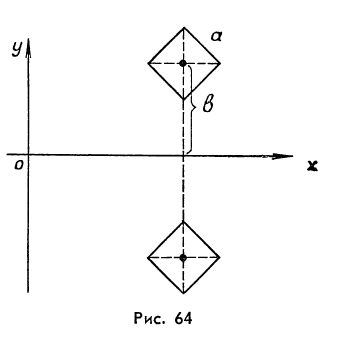
Решение. Центр тяжести C квадрата находится на пересечении его диагоналей. Обозначим через b расстояние центра тяжести Ox. Тогда по второй теореме Гульдина-Паппа искомый объем:
= =2 .