4. Вычисление моментов инерции.
Моментом
инерции материальной точки A
относительно оси l
называется число 
,
где 
- масса точки, а d
- ее расстояние от оси. Аналогично
определяется момент инерции относительно
точки.
Пусть
Г
- материальная линия, линейная плотность
которой во всех точках равна единице.
Тогда масса элементарного участка этой
линии равна его длине dl,
а момент инерции 
такого участка относительно оси абсцисс
равен 
.
Интегрируя, получаем момент инерции
относительно оси абсцисс всей линии:
=
.
Так
же доказывается, что:
=
и 
=
+
,
где
- момент инерции относительно начала
координат.
Отсюда
следует, в частности, что
=
+
.
Есть
линия Г задана параметрическими
уравнениями:
=
,
=
,
0
,
то
=
.
Аналогичные формулы справедливы для и .
Перейдем
к вычислению моментов инерции криволинейной
трапеции. Будем считать, что ее
поверхностная плотность равна единице.
Сначала найдем момент инерции
прямоугольника со сторонами k
и l
относительно стороны k.
Разобьем его на элементарные прямоугольники
со сторонами k
и dy
(см. рис. 61). Площадь (а потому и масса)
каждого такого прямоугольника равна
kdy.
Значит, момент инерции элементарного
прямоугольника относительно этой
стороны выражается формулой: 
=
=
.
Криволинейную
трапецию разобьем на элементарные
прямоугольники со сторонами |y|
и dx.
Момент инерции каждого из этих
прямоугольников относительно оси
абсцисс выражается формулой: 
=
.
Интегрируя, получаем момент инерции
всей криволинейной трапеции относительно
оси абсцисс:
=
.
Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой:
=
- (момент инерции элементарного
прямоугольника относительно оси ординат
равен 
).
Полярный
момент инерции (т.е. момент относительного
начала координат) в этом случае выражается
формулой:
=
+
.
Пример 9. Вычислим момент инерции равнобедренного треугольника относительно его основания.
Решение. Расположим оси координат так, как показано на рисунке 65.
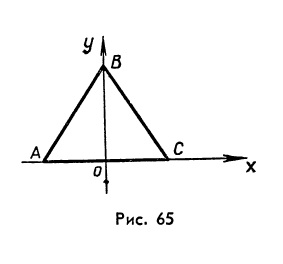
Пусть
основание треугольника |AC|=b,
высота |BO|=h.
Прямая (BC)
проходит через точки B
(0;h)
и C
( 
).
Ее уравнение 
=
,
т.е. y=
.
Ясно, что момент инерции
треугольника ABC
относительно
оси Ox
равен удвоенному моменту инерции
треугольника BOC
относительно той же оси. Значит,:
=
=
-
=
=
.
5. Другие положения интегрального исчисления к физике.
При решении физических задач изучаемый процесс разбивают на элементарные части, в пределах каждой из которых изменением соответствующих величин можно пренебречь. Теперь задача решается по формулам для постоянных величин, после чего окончательный ответ находится с помощью интегрирования.
а) Найдем работу силы при переходе материальной точки из A (a) в B (b), если материальная точка движется по прямой, причем величина силы зависит от координаты x этой точки: F=F (x).
Известно,
что в случае, если сила постоянна, работа
равна F
,
где
- изменение координаты точки. Поэтому
разобьем отрезок [a;
b]
на элементарные части, в пределах каждой
из которых считаем силу постоянной.
Тогда работа силы на участке [x;
x+dx]
равна F
(x)
dx.
Общая работа выражается интегралом:
A=
.
(2)
Пример
10.
Найдем работу, выполняемую при переносе
материальной точки, имеющей массу m,
из A
(a)
в B
(b),
если притягивающая ее по закону Ньютона
точка имеет массу 
и находится в начале координат(рис. 66).
Решение.
По закону Ньютона сила тяготения равна
,
где 
- гравитационная постоянная, а r
- расстояние между точками. По формуле
(2) получаем:
A=
=
.
б) Найдем работу, выполненную двигателем за промежуток времени [a; b], если мощность двигателя в момент времени t равна W (t).
За элементарный промежуток времени [t; t+dt] двигатель имеющий мощность W (t), выполняет работу dA=W (t) dt. Поэтому вся работа двигателя равна:
A=
.