
Математические характеристики распределений случайных величин
1) Математическое ожидание. Определений существует много.
Математическое ожидание:
 – для
дискретных величин. Условие нормировки
– для
дискретных величин. Условие нормировки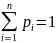
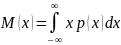 – для
непрерывных величин.
Условие
нормировки
– для
непрерывных величин.
Условие
нормировки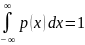
Следствия:
- математическое ожидание случайной погрешности равно нулю.
- за действительные значения случайной величины обычно принимается ее математическое ожидание
2)
Дисперсия
– математическое ожидание квадрата
отклонения случайной величины
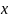 от ее математического ожидания.
от ее математического ожидания.
Для
дискретных величин

Через
вероятность
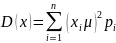
Для
непрерывных величин:
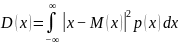
По
определению квадратный корень из
дисперсии называется среднеквадратичным
отклонением.
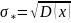
Свойства дисперсии из среднеквадратичного отклонения:
- дисперсия случайной величины положительна
- дисперсия определенной величины равна нулю
-
дисперсия случайной величины равна
разности между математическим ожиданием
квадрата этой величины и квадратом ее
математического ожидания
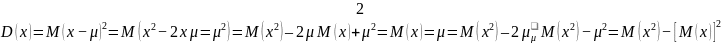 Вместо
Вместо
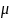 можно
писать
можно
писать
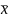 .
.
- дисперсия произведения случайной величины x на множитель c равно произведению квадрата этого множителя на дисперсию x
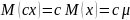
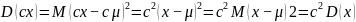 .
Постоянный
множитель можно выносить за знак
среднеквадратичного отклонения.
.
Постоянный
множитель можно выносить за знак
среднеквадратичного отклонения.
- дисперсия суммы независимых случайных величин равняется сумме дисперсий
 Среднеквадратичное
отклонение суммы двух независимых
случайных величин равняется корню из
суммы квадратов этих среднеквадратичных
отклонений
Среднеквадратичное
отклонение суммы двух независимых
случайных величин равняется корню из
суммы квадратов этих среднеквадратичных
отклонений
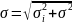
Доверительный интервал и доверительная вероятность
Как
правило находится действительное или
опорное значение случайной величины.
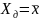 .
Тогда
на оси откладываем
.
Тогда
на оси откладываем
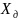 и задаем интервал вокруг него. Назовем
это интервал
и задаем интервал вокруг него. Назовем
это интервал
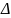 .
.
 – доверительный
интервал.
Величины характеризуется некоторой
вероятностью попадания в этот интервал.
Такая вероятность называется доверительной.
– доверительный
интервал.
Величины характеризуется некоторой
вероятностью попадания в этот интервал.
Такая вероятность называется доверительной.
Можно нарисовать график: Дима тетрадь.
Статистическое описание погрешностей измерения
Роль случайной величины играет погрешность. Раз она случайна, она может характеризоваться некоторой вероятностью. И для нее можно определить, заказать плотность распределения. Эти плотности распределения могут быть разными. Например, бимодальное, равномерное (характерно для цифровых приборов). Таких распределения может быть много.
Наиболее
распространенная плотность вероятности
имеет колокообразный вид. Удачной
аппроксимацией такой зависимости
является нормальное распределение,
описанное уравнением
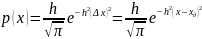
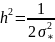
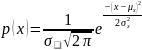
Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты измерений формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительные влияние, по сравнению с суммарным действием всех остальных.
Характеристики нормального распределения или свойства прямой ошибок Гаусса
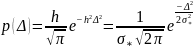
Свойства Гауссовской прямой:
- функция распределения четная
-
при
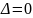 функция
имеет максимум
функция
имеет максимум
-
функция
положительная
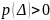
-
график
функции имеет точки перегиба.
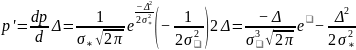
Вторая производная ???
???
-
касательная в точке перегиба отсекает
на оси абсцисс значение
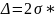 .
Рис 1
.
Рис 1
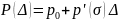
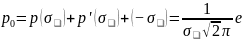 ???
???
В
точке переключения
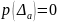

365
-
положение вершины функции
распределения полностью определяется
мерой точности h. Подставив
в перовое выражение получим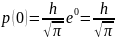 .
Чем выше h,
тем более острый и узкий
пик.
.
Чем выше h,
тем более острый и узкий
пик.
Оценка точности ряда измерений в целом
Пусть
провели ряд измерений некоторой величины
.
Каждое измерение характеризуется своей
погрешностью
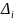 .
Пусть
измерения равноточны, количество n
велико,
и погрешности
распределены
по нормальному закону. Можем говорить
о вероятности того, что
в
интервале
.
Пусть
измерения равноточны, количество n
велико,
и погрешности
распределены
по нормальному закону. Можем говорить
о вероятности того, что
в
интервале
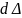 запишется
в виде:
запишется
в виде:
123
Все события независимы, поэтому для определения вероятности их совместного возникновения, мы должны применить теорему об умножении вероятностей.
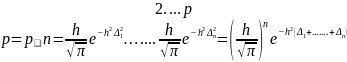 ???
???
Будем искать h, которое характерно для наиболее вероятного события. Для него характерен максимум на функции распределения.
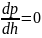 –
условие
максимума.
–
условие
максимума.
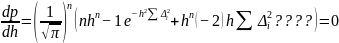 ????
????
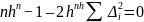
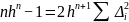
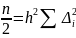

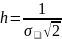 –
Что
и требовалось доказать.
–
Что
и требовалось доказать.
На практике заменяем опорное на какое-либо действительное. В качестве опорного используется среднее арифметическое.
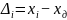
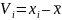
???
Нет звезды. Это реальный параметр, который может рассчитать из экспериментальных данных.
