
10 Задание
1)
Пусть α≤x<+∞,
0≤f(x)≤g(x).
Если
 (x)dx
сходится, то
(x)dx
сходится, то
 (x)dx
тоже сходится
(x)dx
тоже сходится
2)
Если функция f(x)
непрерывна при 0≤x<+∞,
то, по определению,
 (x)dx
равен lim
(x)dx
равен lim (x)dx
(x)dx
3)
Если сходится
 f(x)|dx,
то
f(x)|dx,
то
 (x)dx
тоже сходится
(x)dx
тоже сходится
4)
Если функция f(x)
непрерывна при -∞≤x<b,
то, по определению,
 (x)dx
равен
(x)dx
равен
 (x)dx
(x)dx
5)
Пусть a≤x<+∞,
0≤f(x)≤g(x).
Если
 (x)dx
расходится, то
(x)dx
расходится, то
 (x)dx
тоже сходится
(x)dx
тоже сходится
6)
Если функция f(x)
непрерывна при a≤x≤b
и
 (x)=∞,
то, по определению,
(x)=∞,
то, по определению,
 (x)dx
равен
(x)dx
равен
 (x)dx
(x)dx
7)
Если при α≤x<+∞,
0≤f(x)≤g(x)
и А=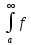 (x)dx<+∞,
а B=
(x)dx<+∞,
а B= (x)dx,
то справедливо соотношение 4
A≤B
(x)dx,
то справедливо соотношение 4
A≤B
8)
Если функция f(x)
непрерывна при x∈[a,c) (c,b],
c∈(a,b)
и функция f(x)
не ограничена в любой окрестности точки
с, то
(c,b],
c∈(a,b)
и функция f(x)
не ограничена в любой окрестности точки
с, то
 (x)dx
равен
(x)dx
равен
 +
+ ]
]
9)
Если функция f(x)
непрерывна при a<x≤b
и
 (x)=∞,
то, по определению,
(x)=∞,
то, по определению,
 (x)dx
равен
(x)dx
равен
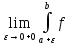 (x)dx
(x)dx
10)
Несобственный интеграл
 (x)dx=
(x)dx= (x)dx
называется сходящимся, если ∃ конечный
предел в правой части ф-ль
(x)dx
называется сходящимся, если ∃ конечный
предел в правой части ф-ль
 (x)dx=
(x)dx=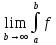 (x)dx
(x)dx
11 Задание
1)
По теореме о среднем значении, для
непрерывной на отрезке [a,b]
функции f
существует точка c∈(a,b),
такая что
 =f(c)(b-a) Док.
E(f)=[m,M],
m=minf[a,b],
M=maxf[a,b],
по т-ме Вейерштрассе: m≤f(x)≤M
∀x∈[a,b].
m(b-a)≤
=f(c)(b-a) Док.
E(f)=[m,M],
m=minf[a,b],
M=maxf[a,b],
по т-ме Вейерштрассе: m≤f(x)≤M
∀x∈[a,b].
m(b-a)≤ (x)≤M(b-a),
m≤
(x)≤M(b-a),
m≤ (x)≤M,
(x)≤M,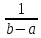 :
: (x)∈[m,M]=E(f)
⇒ ∃c∈[a,b]:
f(c)=
(x)∈[m,M]=E(f)
⇒ ∃c∈[a,b]:
f(c)= ⇒ f(c)(b-a)=
⇒ f(c)(b-a)=
2)
Формулировка теоремы о замене переменной
в неопределенном интеграле такова:
 (x(t))·x’(t)dt=
(x(t))·x’(t)dt= (x)dx|x=x(t) Док.
コF(x)
– первообразная к
f(x)⇒
(x)dx|x=x(t) Док.
コF(x)
– первообразная к
f(x)⇒ (x(t))·x’(t)dt=
(x(t))·x’(t)dt= (x(t))·dx(t)=
(x(t))·dx(t)= (x)dx|x=x(t)=F(x)|x=x(t)+C
(x)dx|x=x(t)=F(x)|x=x(t)+C
3)
Формулировка теоремы об интегрировании
по частям для неопределенного интеграла
такова: dv=uv-
dv=uv- du Док.
du Док.
 dv+
dv+ du=
du= udv+vdu]=
udv+vdu]= d(uv)]=u·v⇒
d(uv)]=u·v⇒ dv=uv-
dv=uv- du
du
4)
Теорема о формуле Ньютона-Лейбница
имеет вид: Если F(x)
– первообр-я непр. ф-и f(x)
на [a,b],
то
 Док.F(x)
и
Док.F(x)
и
 - 2 первообраз. к ф-ииf⇒
1)
- 2 первообраз. к ф-ииf⇒
1) B(1)
x=0:
0=
B(1)
x=0:
0= ⇒c=-F(a)
B(2)
⇒c=-F(a)
B(2)
5)
По теореме об оценке определенного
интеграла, если f(x)
непрерывна на [a,b]
, m
- наименьшее, M
- наибольшее значения f(x)
на [a,b]
, то m(b-a)≤ ≤M(b-a) Док.
m(b-a)=
≤M(b-a) Док.
m(b-a)= ≤
≤ M(b-a)
M(b-a)
6)
По теореме о дифференцировании интеграла
с переменным верхним пределом, если
функция f(x)
непрерывна на отрезке [a,b],
то производная F’(x)=( (t)dt)’
равна f(x) Док.
(t)dt)’
равна f(x) Док. -
- =
= =f(c)
=f(c) ⇒
⇒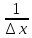 [
[ -
- f(x)
f(x)
7)
Если функции f(x)
и |f(x)|
интегрируемы на [a,b],
то для интегралов
 f(x)|dx
и |
f(x)|dx
и | (x)dx|
верно соотношение |
(x)dx|
верно соотношение | (x)dx|≤
(x)dx|≤ f(x)|dx Док.
|
f(x)|dx Док.
| |=|
|=| +-
+- -|≤
-|≤ ++
++ -=
-= ++f-)=
++f-)=
8)
Формулировка теоремы об интегрировании
по частям в определенном интеграле
имеет вид: (*) dv=uv
dv=uv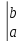 -
- du Док.
du Док.
 dv+
dv+ du=
du= udv+vdu]=
udv+vdu]= d(u·v)]=u·v
d(u·v)]=u·v ⇒(*)
⇒(*)
9)
Если функция f(x)
непрерывна и положительна на отрезке
[a,b],
то для
 (x)dx
выполняется неравенство: Если f(x)≥0
на [a,b],
то
(x)dx
выполняется неравенство: Если f(x)≥0
на [a,b],
то
 (x)dx≥0 Док.
По т-ме о сред. знач.
(x)dx≥0 Док.
По т-ме о сред. знач.
 (x)dx=f(с)(b-a),
где c∈[a,b]
f(x)≥0,
∀x∈[a,b]
⇒ f(c)≥0,
b-a>0
⇒f(с)(b-a)≥0
⇒
(x)dx=f(с)(b-a),
где c∈[a,b]
f(x)≥0,
∀x∈[a,b]
⇒ f(c)≥0,
b-a>0
⇒f(с)(b-a)≥0
⇒ (x)dx≥0
(x)dx≥0
10)
Если функции f
и φ интегрируемы на отрезке [a,b]
и удовлетворяют на нем неравенству
f(x)≤φ(x),
то для интегралов
 (x)dx
и
(x)dx
и
 (x)dx
верно соотношение
(x)dx
верно соотношение
 (x)dx≤
(x)dx≤ (x)dx Док.
(φ(x)-
f(x))≥0
∀x∈(a,b)
⇒ 0≤
(x)dx Док.
(φ(x)-
f(x))≥0
∀x∈(a,b)
⇒ 0≤ =
= -
- ⇒
⇒ (x)dx≤
(x)dx≤ (x)dx
(x)dx
