
- •§ 4. Интегрирование тригонометрических функций
- •1473. Найти интеграл
- •1474. Найти интеграл
- •1475. Найти интеграл .
- •1476. Найти интеграл
- •6. Интегралы вида .
- •1487. Найти интеграл .
- •1488. Найти интеграл .
- •1506. Найти интеграл
- •1507. Найти интеграл
- •1508. Найти интеграл
- •§ 5. Интегрирование разных функций
- •Глава X определенный интеграл
- •§ 1. Вычисление определенного интеграла
- •§ 2. Несобственные интегралы
- •§ 3. Вычисление площади плоской фигуры
- •§ 4. Вычисление длины дуги плоской кривой
- •§ 5. Вычисление объема тела
- •1. Вычисление объема тела по известным площадям поперечных сечений.
- •§ 6. Вычисление площади поверхности вращения
§ 4. Интегрирование тригонометрических функций
1.
Интегралы вида
![]() ,
где
R—
рациональная функция.
,
где
R—
рациональная функция.
Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки tg(x/2) = t.
В результате этой подстановки имеем:
![]()
![]()
![]()
![]()
1472.
Найти
интеграл
![]()
Решение.
Подынтегральная
функция рационально зависит от sin
x
и
cos
x;
применим
подстановку tg(x/2)
= t,
тогда
![]() и
и
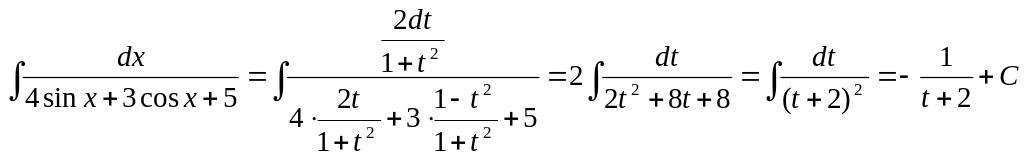
Возвращаясь к старой переменной, получим
![]() ▲
▲
1473. Найти интеграл
Решение.
Полагая tg(x/2) = t, получим
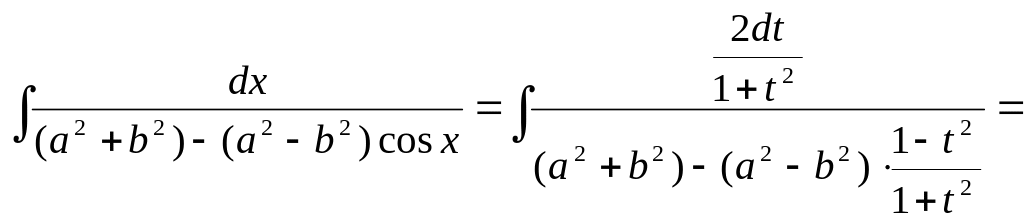
![]()
![]() ▲
▲
Универсальная подстановка tg(x/2)=t во многих случаях приводит к сложным вычислениям, так как при ее применении sin x и соsx: выражаются через t в виде рациональных дробей, содержащих t2.
В некоторых частных случаях нахождение интегралов вида может быть упрощено.
1. Если R(sinx, cos x) — нечетная функция относительно sinx, т. е. если R(—sin x, cosx) =— R (sin x, cosx), то интеграл рационализируется подстановкой cosx = t.
2. Если R(sinx, cosx)—нечетная функция относительно cosx, т. е. если R(sinx, —cosx) = —R (sin x, cos x), то интеграл рационализируется с помощью подстановки sin x = t.
3. Если R (sin x, cos x) — четная функция относительно sin x и cosx, т. е. если R(—sinx, — cosx) = R (sin x, cosx), то к цели приводит подстановка tgx = t.
1474. Найти интеграл
Решение. Так как подынтегральная функция нечетна относительно синуса, то полагаем cosx = t. Отсюда sin2x=1, cos2x = 2 cos2x-1 =2t2-1, dt = - sinxdx. Таким образом,
![]()
![]()
Следовательно
![]()
Отметим, что в рассматриваемом случае интеграл всегда может быть записан виде
![]() ▲
▲
1475. Найти интеграл .
Решение.
Здесь подынтегральная функция является нечетной относительно косинуса. Поэтому применяем подстановку sinx = t; тогда cos2x= 1 — sin2 x = 1— t2, cosxdx = dt. Следовательно,
![]()
Так как
![]()
то
![]()
Окончательно получаем
![]()
Отметим,
что в рассматриваемом случае интеграл
всегда может быть записан в виде
![]() .
▲
.
▲
1476. Найти интеграл
Решение.
Подынтегральная функция четна относительно синуса и косинуса. Полагаем tgx = t; тогда
![]()
Отсюда
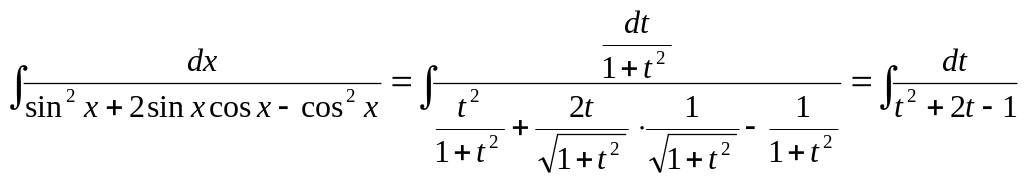 ,
,
Далее имеем
![]()
и, следовательно,
![]()
Заметим, что нахождение интеграла можно упростить, если в исходном интеграле разделить числитель в знаменатель на cos2x:
 ▲
▲
2.
Интегралы
вида
![]() .
Мы выделим здесь два случая, имеющие
особенно важное значение.
.
Мы выделим здесь два случая, имеющие
особенно важное значение.
С л у ч а й 1. По крайней мере одни из показателей т или n —нечетное положительное число.
Если п — нечетное положительное число, то применяется подстановка sinx=t; если же т — нечетное положительное число, — подстановка cosx = t.
1477.
Найти
интеграл
![]() .
.
Решение.
Полагая sinx=t, cosxdx = dt, получим
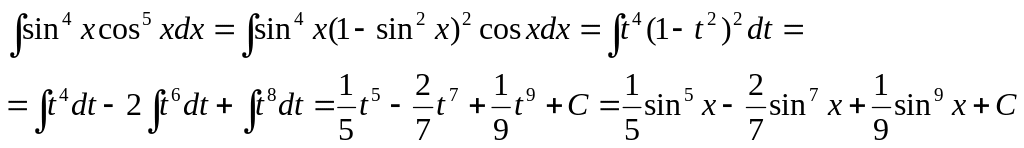
▲
1478.
Найти
интеграл
![]()
Решение.
Имеем
![]()
Полагая cos x = t , — sin x dx = dt, получим

▲
С л у ч а й 2. Оба показателя степени т и n — четные положительные числа. Здесь следует преобразовать подынтегральную функцию с помощью формул
![]() ,
(1)
,
(1)
![]() ,
(2)
,
(2)
![]() .
(3)
.
(3)
1479.
Найти
интеграл
![]()
Решение.
Из формулы (1) следует, что
![]() .
.
Применив теперь формулу (2), получаем
![]() .
.
Итак,
![]() ▲
▲
1480.
Найти интеграл
![]()
Решение. Используя формулу (3), получим
![]() =
=![]()
![]()
=![]()
=![]()
![]()
=![]()
=![]()
1481.
Найти
интеграл
![]()
Решение. Имеем
![]()
![]()
![]()
![]()
3.
Интегралы вида
![]() tgm
x
dx
и
ctgm
x
dx,
где
m
—
целое
положительное
число.
tgm
x
dx
и
ctgm
x
dx,
где
m
—
целое
положительное
число.
При
нахождении таких интегралов применяется
формула
tg2
x
=
sec2
x
—
1
(или ctg2
x
= cosec2
x
— 1),
с
помощью которой последовательно
понижается степень тангенса или
котангенса.
1482.
Найти
интеграл![]()
Решение. Имеем
![]()
![]()
![]()
1483.
Найти интеграл
![]()
Решение. Имеем
![]()
=![]()
=![]()
4.
Интегралы вида
![]() и
и
![]() ,
где
п
— четное
положительное число.
Такие интегралы находятся аналогично
рассмотренным в п. 3 с помощью формулы
,
где
п
— четное
положительное число.
Такие интегралы находятся аналогично
рассмотренным в п. 3 с помощью формулы
sec2 x = 1 + tg2 x (или cosec2 x = 1 + ctg2 x).
1484.
Найти интеграл![]() .
.
Решение. Имеем
![]()
![]()
1459.
Найти
интеграл![]()
Решение. Имеем
![]()
=![]()
5.
Интегралы вида
![]() и
и
![]() .
Интегралы
от нечетной положительной степени
секанса или косеканса проще всего
находятся по рекуррентным формулам:
.
Интегралы
от нечетной положительной степени
секанса или косеканса проще всего
находятся по рекуррентным формулам:
![]() (1)
(1)
![]() (2)
(2)
1460.
Найти
интеграл
![]()
Решение. Применяя рекуррентную формулу (2) при 2n+1=5, т. е. при n = 2, получим
![]()
полагая теперь 2n+1=3, т. е. n=1, по той же формуле имеем
![]()
нo
![]()
Следовательно,
![]()
![]()
