
- •§ 4. Интегрирование тригонометрических функций
- •1473. Найти интеграл
- •1474. Найти интеграл
- •1475. Найти интеграл .
- •1476. Найти интеграл
- •6. Интегралы вида .
- •1487. Найти интеграл .
- •1488. Найти интеграл .
- •1506. Найти интеграл
- •1507. Найти интеграл
- •1508. Найти интеграл
- •§ 5. Интегрирование разных функций
- •Глава X определенный интеграл
- •§ 1. Вычисление определенного интеграла
- •§ 2. Несобственные интегралы
- •§ 3. Вычисление площади плоской фигуры
- •§ 4. Вычисление длины дуги плоской кривой
- •§ 5. Вычисление объема тела
- •1. Вычисление объема тела по известным площадям поперечных сечений.
- •§ 6. Вычисление площади поверхности вращения
6. Интегралы вида .
Тригонометрические формулы
sin
α cos β=
![]() [sin (α + β) + sin (α — β)], (1)
[sin (α + β) + sin (α — β)], (1)
cos α cos β = = [cos (α + β) + cos (α — β)], (2)
sin α sin β= [cos (α— β) —cos(α + β)] (3)
дают возможность произведение тригонометрических функций представить в виде суммы.
1487. Найти интеграл .
Решение. Используя формулу (1), получим
![]()
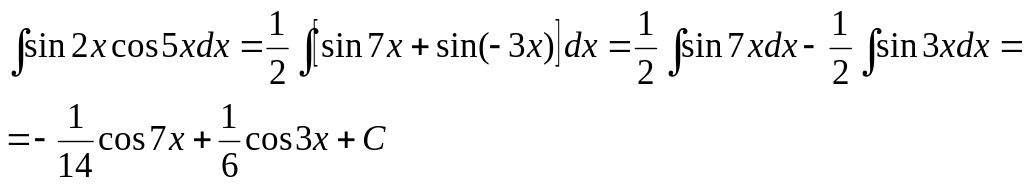
1488. Найти интеграл .
Решение. Применим к произведению cos x cos(x/2) - формулу (2):
![]()
Снова используя ту же формулу, находим
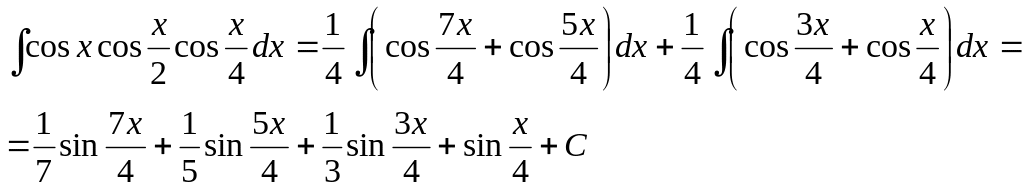
Найти интегралы:
1489.
![]() 1490.
1490.
![]()
1491.
![]() 1492.
1492.
![]()
Указание: положить ctgx=t.
1493.
![]() 1494.
1494.
![]() 1495.
1495.
![]()
1496.
![]() 1497.
1497.
![]()
1498.
![]() 1499.
1499.
![]()
1500.
![]() 1501.
1501.
![]()
1502.
![]() 1503.
1503.
![]()
1504.
![]() 1505.
1505.
![]()
7.
Тригонометрические подстановки.
Интегралы вида
![]()
![]()
![]() приводятся
к интегралам от рациональной относительно
sin
t
и cos
t
функции с помощью надлежащей
тригонометрической подстановки: для
первого интеграла x=a
sin
t
(или x=a
cos
t),
для второго x=a
tg
t
(или x=ctg
t)
и для третьего x=a
sec
t
(или x=acosect).
приводятся
к интегралам от рациональной относительно
sin
t
и cos
t
функции с помощью надлежащей
тригонометрической подстановки: для
первого интеграла x=a
sin
t
(или x=a
cos
t),
для второго x=a
tg
t
(или x=ctg
t)
и для третьего x=a
sec
t
(или x=acosect).
1506. Найти интеграл
Решение. Положим x=a sin t, тогда dx=a cos t dt и заданный интеграл примет вид:
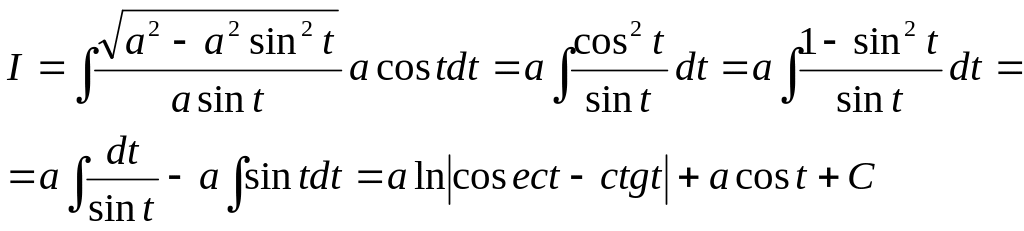
Для
нахождения интеграла
![]() мы
воспользовались формулой
мы
воспользовались формулой
![]() ,
так как с ее помощью легче перейти к
прежней переменной x.
,
так как с ее помощью легче перейти к
прежней переменной x.
Таким образом, получаем
![]()
где
sin
t
= x/a,
![]() .
Следовательно,
.
Следовательно,
![]()
1507. Найти интеграл
Решение. Примерим подстановку x=a tg t , откуда dx=a sec2 t dt. Тогда получим

где
tg
t=x/a
и, следовательно, ctg
t=a/x,
![]()
Итак
![]()
1508. Найти интеграл
Решение. Применим подстановку х = a sec t, откуда dx = a sec t tg t dt. Тогда получим
![]()
Далее применим рекуррентную формулу (1) п. 5 при n=1:
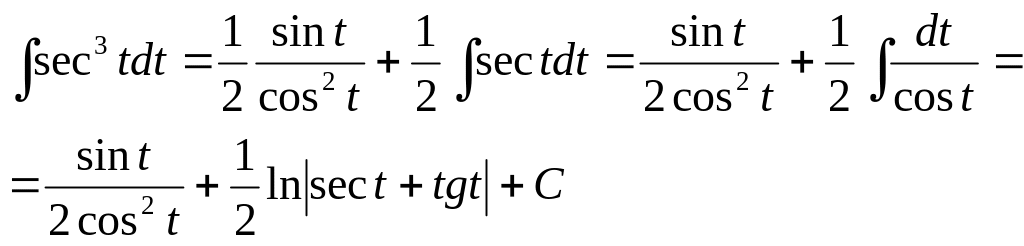
где
![]() .
Следовательно
.
Следовательно
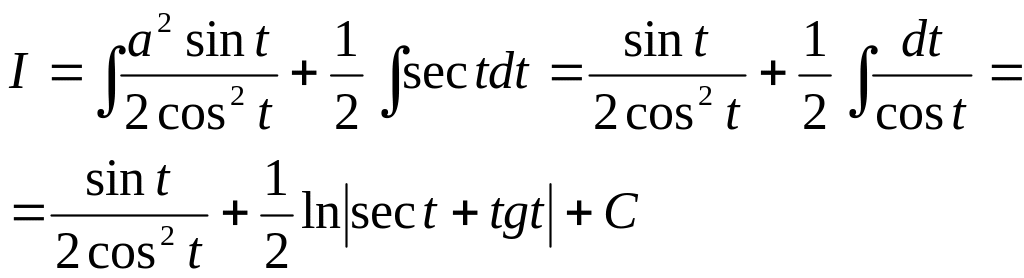
Найти интегралы:
1509.
![]() 1510.
1510.
![]() 1511.
1511.
![]()
§ 5. Интегрирование разных функций
Найти интегралы:
1512.
![]() .
1513
.
1513![]() .
.
1514.
![]() .
1515.
.
1515.
![]() .
.
1516.
![]() 1517.
1517.
![]()
1518.
![]() 1519.
1519.
![]()
1520.
![]() 1521.
1521.
![]()
1522.
![]() 1523.
1523.
![]()
1524.
![]() 1525.
1525.
![]()
1526.
![]() 1527.
1527.
![]()
1528.
![]() 1529.
1529.
![]()
1530.
![]() 1531.
1531.
![]()
1532.
![]() 1533.
1533.
![]()
1534.
![]() 1535.
1535.
![]()
1536.
![]() 1537.
1537.
![]()
Глава X определенный интеграл
§ 1. Вычисление определенного интеграла
Пусть
функция f(х)
определена
на отрезке [а,b].
Разделим
отрезок [а,
b]
на
п
произвольных
частей точками а
= х0
<
х1
< x2
< ... < хп-1
< хп
=
b,
выберем на каждом элементарном отрезке
[xk-1,
xk]
произвольную точку ξk
и найдем длину каждого такого отрезка:
![]() .
.
Интегральной
суммой для
функции f(x)
на отрезке [a,
b]
называется сумма вида
![]() ,причем
эта сумма имеет конечный предел I,
если
для каждого ε>0 найдется такое число
δ>0, что при мах
∆xk<
δ неравенство
|σ-I|<
ε выполняется
при любом выборе чисел ξk.
,причем
эта сумма имеет конечный предел I,
если
для каждого ε>0 найдется такое число
δ>0, что при мах
∆xk<
δ неравенство
|σ-I|<
ε выполняется
при любом выборе чисел ξk.
Определенным интегралом or функции f (х) на отрезке [а, b] (или в пределах от а до b) называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков (мах ∆xk) стремится к нулю:
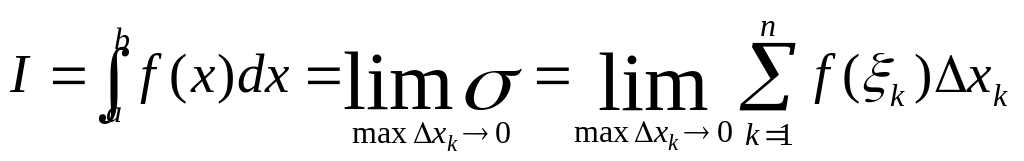
Если функция f(x) непрерывна на [a, b], то предел интегральной суммы существует и не зависит от способа разбиения отрезка [а, b] на элементарные и от выбора точек ξk. (теорема существования определенного интеграла).
Числа a и b соответственно называются нижним и верхним пределами интегрирования.
Если
f(x)>0
на [а,b],
то
определенный интеграл
![]() геометрически
представляет
собой площадь криволинейной
трапеции —
фигуры, ограниченной линиями y
= f(x),
x
= a,
х = b,
у = 0 (рис.
42).
геометрически
представляет
собой площадь криволинейной
трапеции —
фигуры, ограниченной линиями y
= f(x),
x
= a,
х = b,
у = 0 (рис.
42).
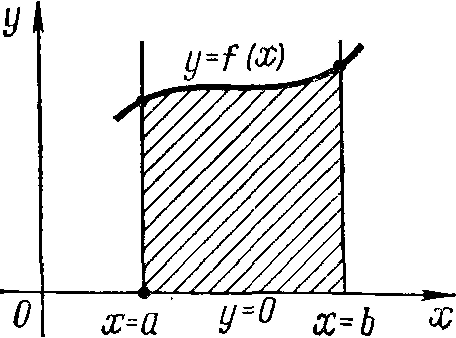
Рис. 42
Основные свойства определенного интеграла
1°.
![]()
2°.![]()
3°.![]()
4°.![]()
5°.![]() ,
где
С- постоянная
,
где
С- постоянная
6°.
Оценка
определенного интеграла: если
![]() на [a,
b],
то
на [a,
b],
то
m(b-a)< <M(b-a)
Правила вычисления определенных интегралов
1. Формула Ньютона — Лейбница:
![]()
где F (х) — первообразная для f(x), т. е. F'(x)=f(x).
2. Интегрирование по частям:
![]()
где и = и(х), v = v (х) — непрерывно дифференцируемые функции на отрезке [а, b].
3. Замена переменной:
где
x=φ(t)
—
функция, непрерывная вместе со своей
производной φ
' (t)
на
отрезке![]() ,
a=φ(α),
b=
φ(β),
f[φ(t)]—
функция,
непрерывная на [α,
β].
,
a=φ(α),
b=
φ(β),
f[φ(t)]—
функция,
непрерывная на [α,
β].
4. Если f(х) — нечетная функция, т. е. f(- х) =-f (х), то
![]()
Если f(х) — четная функция, т. е. f(- x)=f(x), то
![]()
1538.
Вычислить
интеграл
![]() ,
как
предел интегральной суммы.
,
как
предел интегральной суммы.
Решение.
Здесь f(x)
= x2,
а = 0, b
= 1;
разделим отрезок [0,
1]
на n
равных частей, тогда
![]() ,
выберем ξk
=xk.
Имеем:
,
выберем ξk
=xk.
Имеем:
![]()
![]() ;
;
Следовательно,
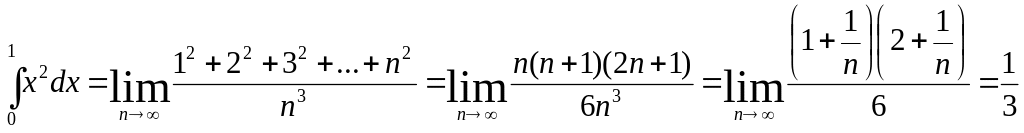
Здесь использована формула суммы квадратов натуральных чисел.
1539.
Вычислить
![]() по формуле Ньютона — Лейбница.
по формуле Ньютона — Лейбница.
Решение.
![]()
1540.
Оценить
интеграл
![]()
Решение.
Так как |cos
x|≤1,
то при x>10
получим неравенство
![]() <10-2.
Следовательно,
<10-2.
Следовательно,
![]() <8*10-2<10-1,
т. е.
<0,1
<8*10-2<10-1,
т. е.
<0,1
1541.
Оценить
интеграл
![]()
Решение.
Поскольку
![]() ,
имеем
,
имеем
![]() и
и
![]()
1542.
Вычислить
![]() .
.
Решение. Воспользуемся методом интегрирования по частям. Положим и = х, dv = e-xdx, откуда du = dx, v = — е-x. Тогда
![]()
1543.
Вычислить
![]()
Решение. Положим ln x=t, тогда (dx)/x=dt, если x=1, то t=0; если x=e, то t=1
Следовательно,
![]()
1544.
Вычислить
![]()
Решение. Положим x = r sin t; тогда dx = r cos t dt; если x = 0, то t=0; если х = r, то t = π/2. Поэтому
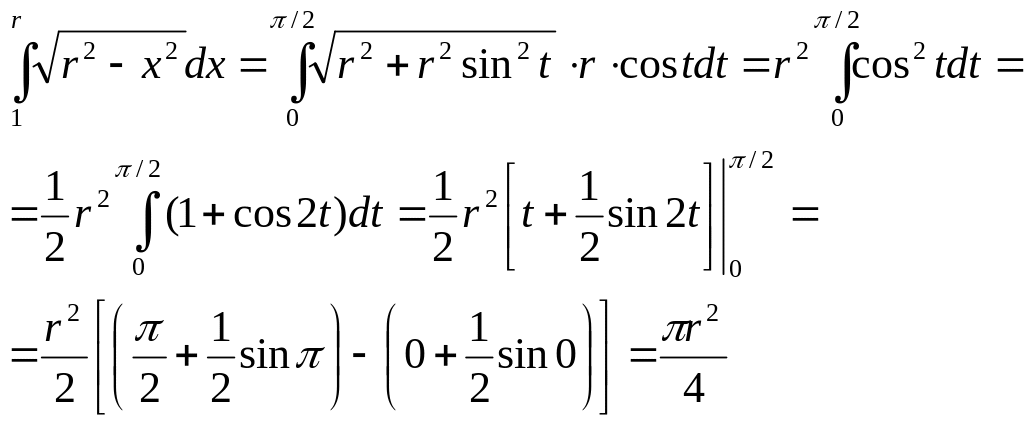
1545.
Вычислить
![]()
Решение.
Подынтегральная функция — четная, а
потому
![]()
Интегрируем
по частям, полагая и
= х,
![]() ;
тогда du
= dx,
v
=1/cosx
;
тогда du
= dx,
v
=1/cosx
Отсюда находим
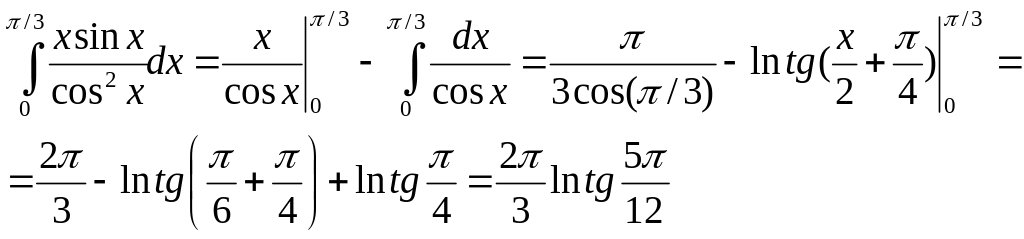
Следовательно,
![]()
1546.
Вычислить
![]() .
.
Решение. Подынтегральная функция—нечетная, следовательно, I= 0.
1547.
Вычислить
![]() как
предел интегральной суммы.
как
предел интегральной суммы.
1548.
Вычислить
![]() как
предел интегральной суммы.
как
предел интегральной суммы.
1549.
Оценить интеграл
![]() .
.
1550.
Оценить интеграл
![]() .
.
1551.
Оценить
интеграл
![]() .
.
Вычислить интегралы:
1552.
![]() 1553.
1553.
![]()
1554.
![]() 1555.
1555.
![]()
1556.
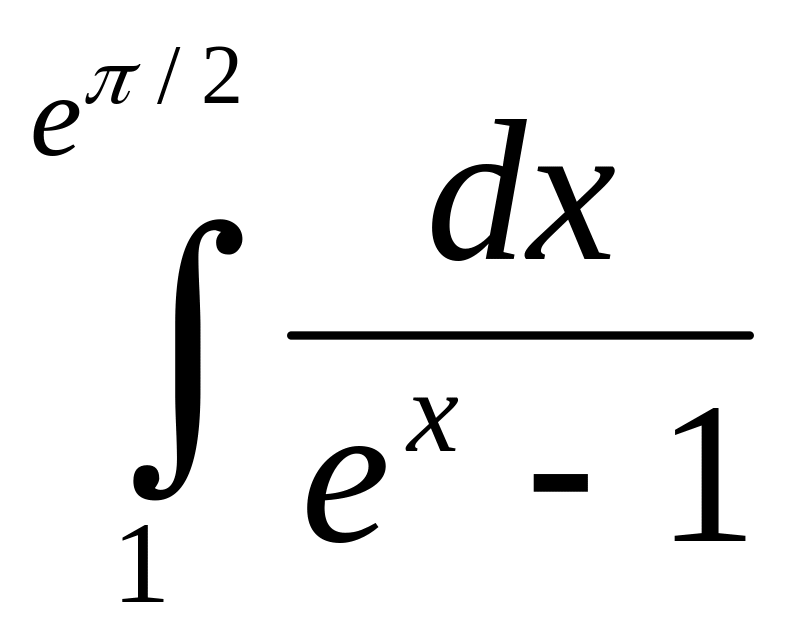 1557.
1557.
![]()
1558.
![]() 1559.
1559.
![]()
1560.
![]() 1561.
1561.
![]()
1562.
![]() 1563.
1563.
![]()
1564.
![]()
Указание: использовать свойство нечетной функции.
1565.
![]()
Указание: использовать свойство четной функции.
1566. Доказать, что
![]()
![]()
![]()
(m и n —целые положительные числа).
