§ 3. Вычисление площади плоской фигуры

Площадь криволинейной трапеции, ограниченно кривой y = f(x) [f (x)≥0], прямыми х = а и х = b и отрезком [а, b] оси Ох, вычисляется по формуле

Площадь фигуры, ограниченной кривыми y = f₁ (х) и y=f₂ (х) [f₁≤f₂ (x)] и прямыми х = а и х = b, находится по формуле

Если кривая задана параметрическими уравнениями x = x(t), y = y(t), то пло­щадь криволинейной трапеции, ограниченной этой кривой, прямыми х = а, х = b и отрезком [а,b] оси Ох, выражается формулой

,

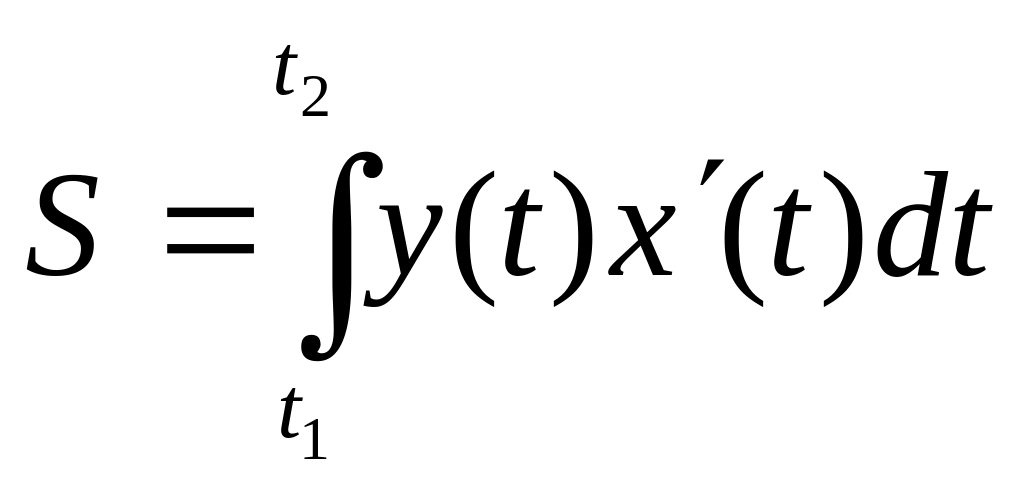где t₁ и t₂ определяются из уравнений a = x(t₁), b=x(t₂) [y(t) ≥0 при t₁≤t ≤t₂].

Площадь криволинейного сектора, ограниченного кривой, заданной в поляр­ных координатах уравнением р = р(0) и двумя полярными радиусами θ = α, θ = β (α < β), выражается интегралом

1592. Найти площадь фигуры, ограниченной параболой у = 4х — x² и осью Ох.

Решение. Парабола пересекает ось Ох в точках 0(0; 0) и М (4; 0). Следо­вательно,

(кв. ед.).

1593. Найти площадь фигуры, ограниченной параболой y=(x-1) ² и гиперболой

x²-y²/2=1.

Решение. Найдем точки пересечения параболы и гиперболы, для чего решим совместно уравнения этих кривых:

или

Левую часть последнего уравнения можно разложить на множители: , откуда x₁=1, x₂=3 и y₁=0, y₂=4. Таким образом, заданные кривые пересекаются в точках A(1;0) и B(3;4). Следовательно,

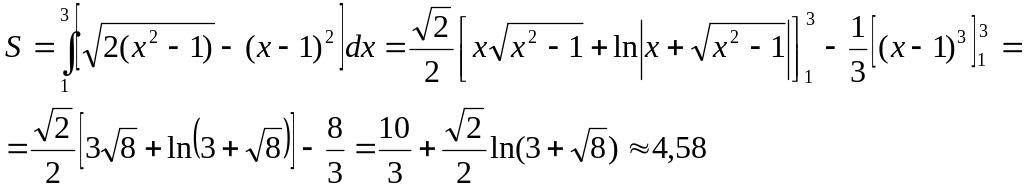
1594. Вычислить площадь плоской фигуры, ограниченной одной аркой циклоиды x = 2(t — sint), y = 2(t— cos t) и осью Ох.

Решение. Здесь dx = 2(1—cost)dt, a t изменяется от t₁ = 0 до t₂ = 2π. Следовательно,

(кв. ед.).

1595. Найти площадь плоской фигуры, ограниченной лемниска­той p² = 2cos2θ.

Решение. Четвертой части искомой площади соответствует изменение θ от 0 до π/4, а потому

(кв. ед.).

Вычислить площади фигур, ограниченных заданными линиями:

1596. у = — х², x+y+2=0

1597. (I четверть).

1598. .

1599. (I четверть).

1600. .

1601. .

1602. .

1603. .

1604. .

1605. .

1606. .

1607. (справа от луча θ = π /2).

1608. (площадь одной петли).

1609. (вне круга р=1).

§ 4. Вычисление длины дуги плоской кривой

Если кривая y = f(x) на отрезке [а, b] — гладкая (т. е. производная y' = f (x) непрерывна), то длина соответствующей дуги этой кривой находится по формуле

При параметрическом задании кривой x = x(t), y = y(t) [x (t) и у (t) — непре­рывно дифференцируемые функции] длина дуги кривой, соответствующая моно­тонному изменению параметра t от t_l до t₂, вычисляется по формуле

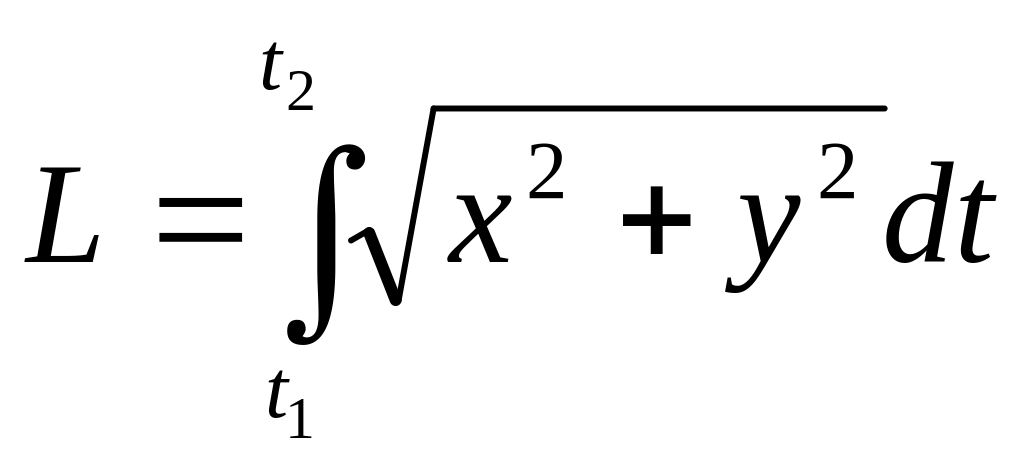
Если гладкая кривая задана в полярных координатах уравнением р=р(θ), α≤θ≤β, то длина дуги равна

1610. Найти длину дуги кривой y² = х³ от x=0 до x=1 (y≥0).

Решение. Дифференцируя уравнение кривой, найдем у' = (3/2) x^1/2. Таким образом,

1611. Найти длину дуги кривой x = cos⁵t, y=sin⁵t от t₁ = 0 до t₂=π/2

Решение. Найдем производные по параметру t: х=—5 cos⁴ t sin t, у = 5 sin⁴t cos t. Следовательно,

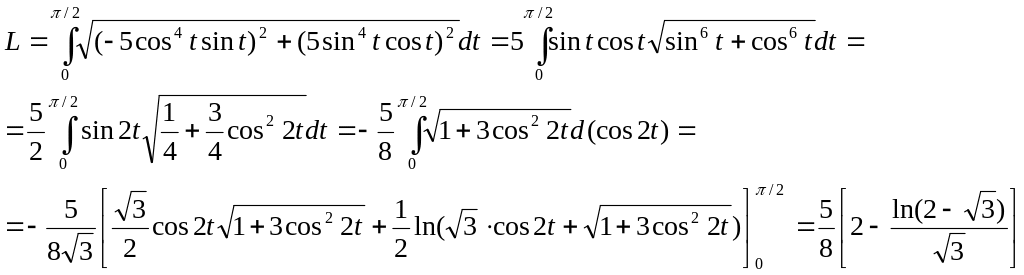
1612. Найти длину дуги кривой р = sin³ (θ/3) от θ₁ = 0 до θ₂ = π /2.

Решение. Имеем р' = sin² (θ /3) cos (θ /3). Следовательно,

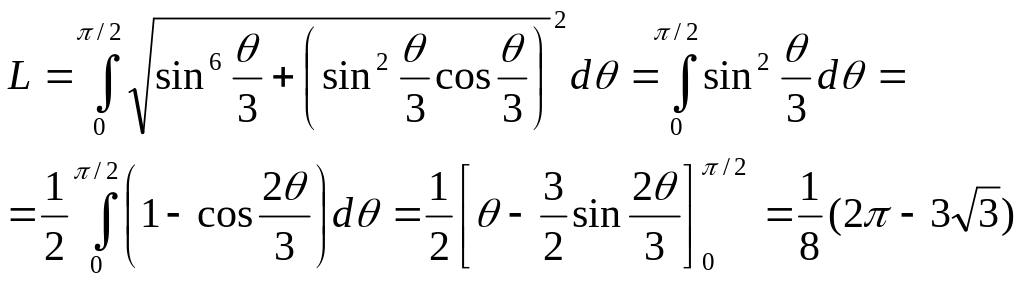
Вычислить длины дуг кривых:

1613. y=ln sin x от x = π /3 до x = π /2.

1614. между точками пересечения с осью Ох.

1615. у = х²/2 от x = 0 до х=1.

1616. y=1-ln cos x от x = 0 до х = π /6.

1617. y=ch x от x=0 до x=1

1618. x=t³/3-t, y=t²+2 от t = 0 до t = 3.

1619. x=e^tcost, y = e^tsint от t = 0 до t = ln π.

1620. x = 8sint+6cost , y=6sint – 8cost x = 0 до х = π /2

1621. x = 9(t — sint), y = 9(l—cost) (длину дуги одной арки циклоиды).

1622. ρ=θ² от θ = 0 до θ = π.

1623. ρ = a sin θ.

1624. ρ = a cos³(θ /3) от θ =0 до θ = π /2.

1625. ρ = l-cos θ.