38 Способы представления графов:

1). Список рёбер (задаётся число вершин и мн-во рёбер, входящих в граф). Объём памяти, необходимый для описания графа не превышает n2 (n – число вершин).

2). Матрица смежности {gij}, n*n. gij={1,(i,j)U;0,(i,j)U;}. Объём памяти <=n2.

3. Матрица инцедентности: {dij}, n*m. Предварительно рёбра нумеруютсяот 1 до m. dij=1, если вершина i инцедентна ребру j и dij=0 в противном случае. Объём памяти n*m<n3.

40 Обходы графов. Алгоритмы поиска в глубину и в ширину. Теорема о поиске в глубину и ширину.

Алгоритм поиска в глубину (в ширину).

(Deep-first search [DFS]. Breadth-first search[BFS])

Вход: Граф G={V,E} задан при помощи списка Г;

Выход: Последовательность вершин; 1)Помечаем все вершины как не пройдѐнные (Х[v] = 0); 2)Выбираем любую вершину графа которая будет корнем обхода, добавляем в структуру Т и помечаем эту вершину как пройдѐнную. 3)Извлекаем вершину u из Т и выдаѐм вершину u на выход алгоритма. 4)Для вершин принадлежащих списку Г, определяем все вершины смежные u, 5)Если они не помечены как пройдѐнные, заносим их в T и помечаем как пройдѐнные, 6)Если Т не пусто выполняем переходим к (3) 7)Если Т пусто завершаем работу алгоритма. Данный алгоритм является поиском в ширину если в качестве Т выбрана Структура Очередь, и поиском в глубину если в качестве Т выбран стек.

Теорема о BFS\DFS:

Если G={V,E} - связный граф, то DFS и BFS обойдѐт все вершины графа ровно по 1 разу.

Доказательство

1) Единственность обхода: Алгоритм обходит лишь те вершины, которые попадают в Т, при попадании в Т вершины помечаются, таким образом каждая вершина будет пройдена не более 1 раза. 2) Конечность алгоритма В структуру Т может попасть не более n вершин, алгоритм гарантированно завершит работу не более чем за n шагов 3) Обход всех вершин Пусть v – начальная вершина обхода. Положим противное – пусть алгоритм завершѐн и существует вершина w из множества V которая не была пройдена, но тогда эта вершина не попадала в Т, а значит не была отмечена, но тогда все смежные ей вершины также небыли отмечены, аналогично для смежных к смежным и т.д., но по условию граф связный, следовательно есть путь между вершинами v и w и значит, что вершина v тоже не отмечена, но это противоречит тому, что вершина v была отмечена на первом шаге.

42.Операции с частями графа.

Пусть G=(N,U), D=(N,W).

Объединением графов G и D: GD наз. граф, представляющий собой объединение мн-в вершин и рёбер исх графов (NM,UW).

Пересечением графов G и D: GD наз. граф (NM,UW).

Произведением графов G и D: G*D наз. граф (NM,UWT), где T={(i,j): iN,jM,ij}.

Операция удаления вершины i из G строится G’=(N\{i},T), где T мн-во тех и только тех рёбер графа G, к-е не инцедентны вершине i.

Операция удаления ребра (i,j). Из G строится G’=(N,U\{(i,j)}).

Операция стягивания вершин по ребру (i,j)U. Результатом будет граф G’, который получается из G след. образом удаляются вершины (i,j) вместе с инцедентными этим вершинам рёбрами, добавляется новая вершина k, к-я смежна тем и только тем вершинам, к-е смежны вершине i или j.

43.Маршруты. Цепи. Циклы. Связность.

Последовательность вершин графа G такая, что любые две соседние вершины в ней смежны, наз. маршрутом.Первая и последняя вершины – концевые. Маршрут, у к-го первая и последняя вершины совпадают наз. замкнутым, в противном случае – открытым. Маршрут, у к-го все рёбра различны наз. цепью. Замкнутая цепь – цикл. Цепь у к-й все вершины различны, наз. простой. Цикл, у к-го все вершины кроме первой и последней различны –простой. Граф наз. связным, если из любой его вершины можно попасть в любую по некоторому маршруту. Максимально по по вклюцению связный подграф графа G наз. компонентой связности.

Алгоритм распознования связности графа.

Пусть граф задан матрицей смежности. Необходимо выяснить, является ли он связным.G=(N,U), M-рабочее мн-во.

M:=. Выбираем произвольную вершину графа i и заносим её в M.

Формируем мн-во P всех таких вершин ккоторые не не вошли в M и каждая из которых смежна по крайней мере одной вершине из M.

Если P, то расширяем мн-во M: M:=MP и возвращаемся в п.2.

Если M=N, то исх. граф связен. Конец работы.

Иначе G – не связный граф и G(M) – компонента связности. Конец работы.

Оценим сложность работы алгоритма. Под сложностью работы алг. будем понимать число эл. действий, необходимых для его реализации. Оценим сложность алгоритма в виде ф-и от размерности графа. Пусть граф имеет k вершин. Предположим, что мы находимся на некотором шаге работы алгоритма. Оценим число действий, необх. Для построения мн-ва P. nM. Для постр. мн-ва P необходимо просмотреть всевозможные пары (i,j) и выбрать среди них такие, что iM, jM, (i,j)U. Число таких пар <=n2. Для построения мн-ва P потребуется <=n2 операций. Всего таких процедур <=n. Поэтому число эл. действий, необходимых для распознования связности графа ограничено n3, т.е. алгоритм имеет сложность порядка n3. (0(n3)).

49Эйлеровы цепи.Пусть G=(V,E)- граф. Цикл, который включает все ребра и вершины графа G, называется эйлеровым циклом.

Цикл, содержащий все ребра мультиграфа называется эйлеровым, и мультиграф, в котором имеется эйлеров цикл, также называется эйлеровым.

Связанный неориентированный мультиграф тогда и только тогда эйлоровым, когда степень каждой из его вершин – четное число.

Алгоритм построения эйлерова цикла в эйлеровом мультиграфе:

1. выбрать некоторую вершину а

2. выбрать некоторое ребро u, инцидентная а, и присвоить ему номер1 (пройденное ребро).

3. Каждое пройденное ребро вычеркнуть и присвоить ему номер на 1 больше номера предыдущего вычеркнутого ребра.

4. Находясь в вершине х не выбирать ребро соединяющее х с а, если имеется возможность иного выбора.

5. Находясь в вершине х не выбирать ребро, которое является перешейком (т.е. ребром, при удалении которого граф, образованный не вычеркнутыми ребрами распадается на две компоненты связанности, каждая из которых имеет хотя бы по 1 ребру).

6. После того как в графе будут занумерованы все ребра образуется эйлеров цикл, причем порядок нумерации соответствует последовательности обхода ребер.

Цепь, содержащая все ребра графа называется эйлеровой.

50. Цикл графа G, содержащий все его рёбра, наз. эйлеровым. Граф, имеющий эйлеров цикл наз. эйлеровым.

Терорема.

Для каждого связного графа G следующие условия эквивалентны:

G – эйлеров граф.

Каждая вершина графа G имеет чётную степень.

Мн-во рёбер графа можно разбить на простые циклы, т.е. U=ki=1 ui (ui uj=, (ij), ui=).

Доказательство.

Пусть G – эйлеров граф. Покажем, что каждая вершина имеет чётную степень. Каждая вершина простого цикла имеет степень 2. Поэтому, если в графе G существует эйлеров цикл, то каждая вершина должна иметь чётную степень.

Пусть каждая вершина имеет чётную степень. Выбираем произвольную вершину графа i1 и движемся от неё по ребру к смежной вершине i2, и т.д. каждый раз выбирая новое ребро. Т.к. граф связен, число рёбер в графе конечно и войдя в вершину по некоторому ребру мы можем выйти по другому, то через некоторое число шагов какая-то вершина ik повторится. Тогда i1,i2,…,ik,i1 образует простой цикл в исодном графе (u1). Удалим рёбра этого цикла из исходного графа. Новом графе каждая не изолированя вершина имеет чётную степень, поэтому процедуру выделения простых циклов можно применять к каждой компоненте связности, отличной от изолированой вершины. Через некоторое число шагов мы получим исх. разбиение.

Пусть закдано разбиение U=ki=1 ui. Покажем, что  эйлеров цикл. Т.к. G – связный граф, то найдутся два простых цикла имеющих общую вершину эти два цикла можно объеденить (склеить) в один цикл. Пусть u’ и u’’ имеют общую вершину k. u’=(j1,j2,…,jl-1,k,j1+1,…,jm,j1), u’’=(t1,t2,…,td-1,k,td+1,…,tf,t1), u*=(j1,j2,…,jl-1,k,td-1,…,t1,tf,tf-1,…,td+1,k,j1+1,…,jm,j1). Число циклов при этом уменьшиться на еденицу. Повторяя процедуру склеивания, в итоге получим один цикл, содержащий все рёбра исходного графа – эйлеров цикл, ч.т.д.

Док-во данной теоремы можно использовать в качестве алгоритма при построении эйлерового цикла, если он существует.

51.Эйлеровым путем(цепью) в графе называется путь, проходящий через каждое ребро графа только один раз, т.е. путь v1,v2..., vm+1, такой, что каждое ребро e, принадлежащее E, появляется в последовательности v1, v2..., vm+1 в точности один раз как e={vi,vi+1}. В этом случае говорят, что граф G имеет эйлеров путь. Если граф G связный и А и В единственные нечётные вершины его, то граф G обладает эйлеровым путём с концами А и В.

Задача существования эйлерова пути в заданном графе была решена Л.Эйлером в 1736 г., и представленное им необходимое и достаточное условие существования такого пути считается первой в истории теоремой теории графов.

Если эйлеров путь не является эйлеровым циклом, то такой путь назы-

вают собственным эйлеровым путем.

ТЕОРЕМА. Граф (мультиграф или псевдограф) имеет собственный

эйлеров путь тогда и только тогда, когда он связный и ровно две его вершины

имеют нечетную степень.

Пример 1. Рассмотрим граф

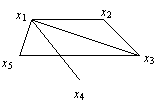
Он имеет эйлеров путь (x4, x1, x3, x2, x1, x5, x3).

Пример2. Граф имеет собственый Эйлеров путь.

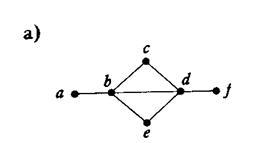
Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Эйлеров граф — граф, содержащий эйлеров цикл.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

Эйлеров цикл/путь существуют только в связных графах или в графах, которые после удаления всех одиночных вершин превратятся в связные.

Теорема:

О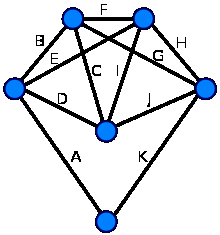 риентированный граф содержит эйлеров цикл тогда и только тогда, когда он сильно-связан и для каждой вершины графа её полустепень захода равна её полустепени исхода, то есть в вершину входит столько же ребер, сколько из неё и выходит.

Пример:

52 Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.

Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом.

59 Орграфы. Основные понятия.

Орграфом называется пара множеств, элементы первого множества называются вершины, элементы второго называются дугами.

Множество дуг — это множество упорядоченных пар вершин.

(i,j)≠(j,i)

i- начало дуги, j — конец дуги.

Число дуг входящих в вершину — полустепень захода.

Полустепень исхода — число дуг, выходящих из вершины.

Орграф называется простым, если он не имеет параллельных дуг, в противном случае он называется мультиграфом.

Нормальным упорядочением вершин орграфа называется такое их упорядочение, при котором всегда (i1, i2 ... in) если имеется пара (ik; in), то вершина ik в упорядочении стоит раньше in. В общем случае имеет место не одно нормальное упорядочение для графа.

Теорема: Пусть задан орграф G = (V,E), тогда следующие утверждения являются эквивалентными.

1) Граф G — безконтурный.

2) Граф G обладает рекурентными свойствами нормальной упорядочености: если множество вершин графа не пусто, то существует вершина не имеющая входящих дуг и после удаления такой вершины обновленный граф также будет иметь свойства нормальной упорядочености.

3) Множество упорядочений графа G не пусто.

Существуют два основных метода представления графов в памяти ЭВМ: матричный, т.е. массивами, и связными нелинейными списками. Способы представления матричным методом: матрица смежности, массив ребер, матрица инцидентности, списки смежности.

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы сответствуют вершинам, строки — ребрам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). В каждой строке должны стоять две единицы, а все остальные символы - нули.

Пример

Матрица смежности графа G с конечным числом вершин n — это квадратная матрица A размера n, в которой значение элемента aij равно числу ребёр из i-й вершины графа в j-ю вершину. Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i-й вершины. Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали. Матрица смежности полного графа Kn содержит единицы во всех своих элементах, кроме главной диагонали, на которой расположены нули. Матрица смежности пустого графа, не содержащего ни одного ребра, состоит из одних нулей. Степени матрицы. Если A — матрица смежности графа G, то матрица A в степени m обладает следующим свойством: элемент в i-й строке, j-м столбце равен числу путей из i-й вершины в j-ю, состоящих из ровно m ребер.

Пример

Списки смежности. Представляет собой структуру данных, которая для каждой вершины графа хранит список смежных с ней вершин. Список представляет собой массив указателей, i-ый элемент которого содержит указатель на список вершин, смежных с i-ой вершиной. Список смежности более эффективен по сравнению с матрицей смежности, так как исключает хранение нулевых элементов.

Теорема(Эйлера формула)

Если G связный планарный граф, содержащий V вершин, e ребер и f граней, то V-e=f=2

Доказательство

Докажем формулу Эйлера по индукции по числу ребер в

1. Пусть е=0, тогда V=1, f=1 формула действительна

Пусть е=1, тогда V=2, f=1 формула действительна

2. Индукциальная гипотеза:

Предположим, что теорема верна для произвольного связного планарного графа, у которого k ребер.

3. Индукционный переход

Пусть задан G_k+1 , имеющий е= k+1. Проверим выполнимость формулы для этого графа. Удалим одно ребро графа G_k+1, так что в результате будет получен граф G_k , для которого выполняется формула.

А. Предположим что граф G_k+1 не имеет циклов. Будем перемещаться вдоль по пути до тех пор, пока не достигнем вершины, у которой нет другого выходящего ребра. Это обязательно произойдет, так как граф не содержит циклов, найденная вершина будет иметь степень 1. Удалим ее и ребро, инцидентное ей. Очевидно, что f не изменится. При этом граф останется связным, планарным, а значит формула выполняется. Поскольку количество вершин и ребер начального графа >1 , то значение выражения V-e=f=2 после процедуры удаления останется неизменным. Таким образом для G_k+1, V-e=f=2 и в этом случае теорема доказана.

Б. Граф G_k+1 имеет цикл. Удалим из него ребро е и инцидентное вершинам V_і и U_i . Очевидно, что е_і не является разрезающим, таким образом между V_і и U_i остаётся путь и граф связный. Граф также останется планарным и содержит k ребер. Поэтому для оставшегося графа по индукциальной гипотезе формула выполняется. Покажем что она выполняется и для графа G_k+1. Поскольку е і входило в цикл, она разделяло 2 грани. поэтому V-e=f=2 не изменилось, формла справедлива и для G_k+1.

Для доказательства того, что полный двудольный граф К₃₃ является моделью задачи о трех домах и трех колодцах, не может быть изображен без пересечения ребер.

Т2:Полный двудольный граф К₃₃ не является планарным

Доказательство.

Предположим, что К₃₃ планарен. В графе V=6 е=9. Если он планарен, то по формуле Эйлера 6-9+ f=2 он имеет 5 граней. Пусть А и В не пресекается непересекающиеся мноножества вершин формирующие V графа графа К₃₃ V=АvВ .

Если начать путь из одного из непересекающихся множества А и не повторять ребра, то можно попасть в вершину из множества В вернуться в А , вернуться в В, попасть в А вернуться в Ви завершить цикл. Таким образом каждый цикл в К₃₃ представляет собой путь длинны U. Поэтому каждая грань определена циклом в котором не менее 4 ребер. Следовательно, сумма ребер во всех гранях > f. Однако каждое ребро пренадлежит граням U учитывается не более 2-х раз. Значит сумма ребер всех граней <2e . полученые неравенства объеденим 4f<=2e => f<=4. Это противоречит f=5.

Для доказательства того, что К5 не планарен сформулируем и докажем лемму.

Лемма 1:

В производном связном планарном графе G с V>3 имеет место3V-e>=6

Доказательство

Пусть G имеет цикл. Будем суммировать ребра, ограничивающее грани в G. Поскольку каждая грань включает не менее 3 ребер, то сумма всех граней > 3f. С другой стороны каждое ребро является границей двух граней. Поэтому сумма всех ребер <2е. Следовательно 3f<=2e. Так как граф связный и планарный, справедлива формула Эйлера

V-e=f=2

3V-3e+3f<=3V-3e+2e

3V-3e+3f<=3V-e

3V-e>=6

Т:Полный граф К5 не планарен.

Доказательство

Граф К5 связний и имеет количество ребер e=n(n-1)/2

е=10 V=5

Таким образом по предыдущей лемме

3V-e>=6 К5 – не планарен

Т: Каждый планарный граф содержит вершину V степени 5 или менее.

Доказательство

Каждое ребро графа имеет 2 вершины. Таким образом оно вносит 2 ед в сумму степеней всех вершин.

Если в графе не более 2-х вершин, то очевидно каждая из них имеет 5 или менее. Пусть в графе 3 или более вершин. Тогда по лемме 1 3V-e>=6. Таким образом, если предположить, что степень каждой вершины >=6, то сумма степеней всех вершин >= 6V, но по условию 2е >=6 V, но это невозможно, поскольку 2е <=6V-12, следовательно существует вершина со степенью 5 или меньше.

Лемма2 :

Если 2 связных графа гомеоморфны, то они оба либо планарны, либо оба не планарны.

Лемма3:

Произвольный граф, гомеоморфный графу К33 или К5 непланарен

Теорема Куратовского:

Граф G является планарным тогда и только тогда, когда он не содержит подграф, гомеоморфный графу К33 или К5.