1. Математическая модель. Классификация и принципы построения математических моделей. Примеры задач, решаемых методами математического программирования.

Математическая модель – это система математических соотношений, приближённо, в абстрактной форме описывающих изучаемый процесс или систему.

Экономико-математическая модель – это математическая модель, предназначенная для исследования экономической проблемы.

Перечислим некоторые основные принципы построения математической модели.

1. Необходимо соизмерять точность и подробность модели, во-первых, с точностью тех исходных данных, которыми располагает исследователь, и

во-вторых, с теми результатами, которые требуется получить.

2. Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.

3. Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы. Если при этом получаются сходные результаты, то исследование заканчивается. Если результаты сильно различаются, то следует пересмотреть постановку задачи.

4. Любая сложная система всегда подвергается малым внешним и внутренним воздействиям, следовательно, математическая модель должна быть устойчивой, т.е. сохранять свои свойства и структуру при этих воздействиях.

По числу критериев эффективности математические модели делятся на однокритериальные и многокритериальные. Многокритериальные математические модели содержат два и более критерия.

По учёту неизвестных факторов математические модели делятся на детерминированные, стохастические и модели с элементами неопределённости.

2. Постановка и различные формы записи задач линейного программирования. Множество допустимых решений. Оптимальное решение задачи линейного программирования.

В общем виде задача линейного программирования ставится следующим образом.

Максимизировать (минимизировать) функцию

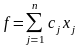
(1)

при ограничениях

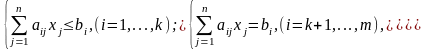(2)

где 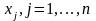- управляющие переменные или решения задачи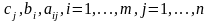 - параметры,

f – целевая функция или критерий эффективности.

Функция (1) – линейная, ограничения (2) – тоже линейные. Задача содержит n переменных и m ограничений.

3. Стандартная и каноническая формы представления задач линейного программирования.

В канонической форме записи все переменные неотрицательны, ограничения являются уравнениями, и требуется найти такие значения , при которых целевая функция имеет максимум.

4. Геометрическая интерпретация задач линейного программирования. Многогранник решений. Алгоритм решения задачи линейного программирования графическим методом.

Выпуклое замкнутое множество точек пространства (плоскости) называется выпуклым многогранником (многоугольником).

Алгоритм решения задачи линейного программирования графическим методом:

1) Записывают уравнения прямых, соответствующих ограничениям, и строят их на плоскости .

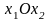2) Определяют области, в которых выполняются ограничения задачи. Для этого выбирают произвольную точку на плоскости и подставляют её координаты в левую часть одного из неравенств. Если неравенство, верно, то искомая полуплоскость находится с той же стороны от прямой, что и точка; в противном случае искомая полуплоскость лежит с противоположной стороны от прямой. Эти действия последовательно выполняются для всех неравенств.

3) Определяют область допустимых решений задачи как область пересечения m полуплоскостей, соответствующих m ограничениям задачи. Область допустимых решений представляет собой многоугольник (ограниченный или нет), либо пустое множество. Экстремальные значения целевой функции достигаются в угловых точках области допустимых решений.

4) Определяют направление возрастания (убывания) целевой функции f. Для этого строят вектор – градиент целевой функции 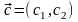, его направление показывает направление возрастания функции f, в противоположном направлении функция убывает.

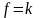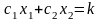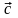5) Строят линию уровня целевой функции , где - некоторая константа (т.е. ), перпендикулярную вектору и походящую через область допустимых решений. Передвигают ее в направлении вектора (или в противоположном вектору направлении в задачах на минимум) параллельно самой себе до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты данной точки и определяют оптимальный план данной задачи.

6) Вычисляют координаты найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.