
- •Математическая модель. Классификация и принципы построения математических моделей. Примеры задач, решаемых методами математического программирования.
- •Постановка и различные формы записи задач линейного программирования. Множество допустимых решений. Оптимальное решение задачи линейного программирования.
- •Стандартная и каноническая формы представления задач линейного программирования.
- •Геометрическая интерпретация задач линейного программирования. Многогранник решений. Алгоритм решения задачи линейного программирования графическим методом.
- •Геометрический смысл симплекс-метода решения задач линейного программирования. Построение начального опорного плана.
- •Симплекс-метод. Критерий оптимальности опорного плана.
- •Симплекс-метод. Правило перехода к новому опорному плану.
- •Симплекс-таблица. Пересчет симплекс-таблиц. Алгоритм симплекс-метода решения задач линейного программирования.
- •Метод искусственного базиса.
- •Экономическая интерпретация двойственных задач планирования производства.
- •Двойственная задача линейного программирования и алгоритм её формирования.
- •Формулировка теоремы двойственности. Нахождение оптимального плана двойственной задачи.
- •Анализ модели на устойчивость по отношению к изменениям запасов продукции (основная теорема).
- •Экономическая и математическая формулировки транспортной задачи.
- •Закрытая и открытая модели транспортной задачи. Приведение открытой транспортной задачи к закрытой.
- •Методы построения начального опорного плана транспортной задачи: метод северо-западного угла и метод минимального элемента.
- •Вырожденные и невырожденные планы транспортной задачи. Система потенциалов, экономический смысл. Критерий оптимальности опорного плана транспортной задачи.
- •Получение оптимального плана транспортной задачи с помощью метода потенциалов.
- •Алгоритм улучшения плана транспортной задачи. Понятие цикла, пересчет по циклу. Снятие вырожденности плана.
- •Транспортные задачи с ограничениями на пропускную способность сети.
- •Матричные игры. Платежная матрица. Игра с нулевой суммой.
- •Принцип минимакса и максимина. Верхняя и нижняя цена игры.
- •Оптимальные стратегии игроков. Решение матричной игры с седловой точкой.
- •Чистые и смешанные стратегии игроков. Вероятностная интерпретация. Теорема о существовании решения игры в смешанных стратегиях (теорема о минимаксе).
- •Графическое решение в случае игры 2 m и n2 .
- •Сведение решения игры в произвольном случае к задаче линейного программирования.
- •Математические модели межотраслевого баланса. Матрицы прямых и полных производственных затрат.
- •Валовой, конечный и чистый продукты. Определение цены конечной продукции.
- •Определение себестоимости продукции.
Двойственная задача линейного программирования и алгоритм её формирования.
Формулировка теоремы двойственности. Нахождение оптимального плана двойственной задачи.
Теорема
двойственности.
Если одна из взаимно двойственных задач
имеет оптимальное решение
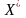 ,
то другая также имеет оптимальное
решение
,
то другая также имеет оптимальное
решение
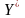 .
При этом соответствующие им оптимальные
значения целевых функций
.
При этом соответствующие им оптимальные
значения целевых функций
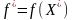 и
и
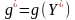 равны.
равны.
Анализ модели на устойчивость по отношению к изменениям запасов продукции (основная теорема).
Двойственные оценки тесным образом связаны с оптимальным планом прямой задачи. Всякое изменение исходных данных прямой задачи может оказать влияние как на её оптимальный план, так и на систему двойственных оценок. Поэтому, чтобы проводить экономический анализ с использованием двойственных оценок, нужно знать их интервал устойчивости.
Свойство устойчивости в общем случае – это сохранение оптимальности решения при небольших изменениях параметров. Устойчивость модели играет важную роль на практике. Если значение оптимального решения резко изменяется при небольших отклонениях параметров, то такой моделью сложно пользоваться на практике, где изменения цен и запасов – явление обыденное.
При анализе устойчивости необходимо дать ответы на следующие вопросы.
1. На сколько могут быть увеличены запасы дефицитных ресурсов для улучшения оптимального плана при сохранении общей структуры решения?
2. На сколько могут быть снижены запасы дефицитных ресурсов при сохранении общей структуры оптимального решения?
3. Какие дефицитные ресурсы следует увеличивать в первую очередь?
4. На сколько могут быть снижены запасы недефицитных ресурсов при сохранении оптимальности полученного решения?
5. Каковы пределы изменения коэффициентов целевой функции, при которых не происходит изменения оптимального плана?
6. На сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать дефицитный ресурс недефицитным и наоборот?
Предположим, что прямая задача имеет невырожденные опорные планы и хотя бы один из них является оптимальным.
Максимальное
значение целевой функции прямой задачи
будем рассматривать как функцию
свободных членов системы линейных
уравнений:
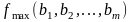 .
.
Теорема.
В оптимальном плане двойственной задачи
значение переменной
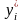 численно равно частной производной
функции
по данному аргументу, т.е.
численно равно частной производной
функции
по данному аргументу, т.е.
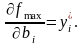
Последнее
равенство означает, что изменение
значений величин
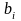 приводит к увеличению или уменьшению
.
Это изменение
определяется величиной
приводит к увеличению или уменьшению
.
Это изменение
определяется величиной
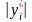 и может быть охарактеризовано лишь
тогда, когда при изменении величин
значения переменных
в оптимальном плане соответствующей
двойственной задачи остаются неизменными.
Поэтому представляет интерес определить
такие интервалы изменения каждого из
свободных членов системы линейных
уравнений прямой задачи, в которых
оптимальный план двойственной задачи
не меняется. Это имеет место для всех
тех значений
и может быть охарактеризовано лишь
тогда, когда при изменении величин
значения переменных
в оптимальном плане соответствующей
двойственной задачи остаются неизменными.
Поэтому представляет интерес определить
такие интервалы изменения каждого из
свободных членов системы линейных
уравнений прямой задачи, в которых
оптимальный план двойственной задачи
не меняется. Это имеет место для всех
тех значений
 ,
при которых столбец свободных членов
последней симплекс-таблицы решения
задачи не содержит отрицательных чисел,
т.е. тогда, когда среди компонент вектора
,
при которых столбец свободных членов
последней симплекс-таблицы решения
задачи не содержит отрицательных чисел,
т.е. тогда, когда среди компонент вектора
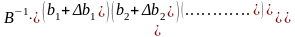
нет отрицательных. Здесь В-1 - матрица, обратная матрице В, составленной из компонент векторов базиса, который определяет оптимальный план задачи.
