1. Группы, кольца. Примеры, основные свойства. Кольцо целых чисел. Теорема о делении с остатком. Наибольший общий делитель и наименьшее общее кратное.

Бинарной (алгебраической) операцией на множестве А называют соответствие, сопоставляющее каждой упорядоченной паре (a, b) элементов множества А единственный элемент с того же множества. Кроме бинарных операций существуют нольарные, унарные, тернарные, n-арные и т.д. Бинарная операция  называется коммутативной, если для любых двух элементов a, b из множества А выполняется: ab = ba.Бинарная операция  называется ассоциативной, если (a, b, сА) (ab)с = a(bс). Пусть на множестве А заданы 2 бинарные операции: (А,,). Бинарная операция  называется дистрибутивной относительно операции , если: (a, b, сА) (ab)с = (aс)(bc) (правая дистрибутивность) и с(ab) = (са)(сb) (левая дистрибутивность). Элемент nА называется нейтральным относительно бинарной операции , заданной на А, если (aА) an = nа = а. Теорема (о единственности нейтрального элемента): если нейтральный элемент относительно бинарной операции существует, то он единственный. Д-во( МОП): пусть n₁ и n₂ – 2 нейтральных элемента относительно одной и той же операции . n₁n₂ = n₂  n₁n₂ = n₁  n₁ = n₂.

Пусть  - бинарная операция на множестве А, имеющая нейтральный элемент n. Элемент а называется симметричным для элемента а, если выполняется условие: аа = аа = n. Теорема (о числе симметричных элементов у ассоциативной операции): если операция  ассоциативна, то никакой элемент не может иметь более одного симметричного элемента.

Для бинарных операций наиболее распространенными являются следующие 2 формы записи: аддитивная и мультипликативная. Множество А с одной или несколькими заданными в нем алгебраическими операциями называется алгеброй (алгебраической системой). Наиболее важными типами алгебр являются: группы, кольца, поля, векторные пространства. Отображение первой алгебры на вторую, сохраняющее операции, называется гомоморфизмом. При этом вторая алгебра называется гомоморфным образом первой алгебры. Взаимнооднозначный гомоморфизм первой алгебра на вторую называется изоморфизмом.

Непустое множество G с алгебраической операцией  на нем называется группой, если: 1)  ассоциативна, 2) относительно  имеется нейтральный элемент, 3) для любого элемента из множества G имеется симметричный. Примеры групп: (Z,+). Не являются группами: (N,+), (Z, ), (Q,). Полугруппу с единичным (нейтральным) элементом называют моноидом. Свойства групп: 1) единица единственная Д-во: следует из теоремы о единственности нейтрального элемента., 2) обратные элементы единственные. Д-во: по теореме о числе симметричных элементов у ассоциативной операции для любого элемента а может быть не более одного симметричного. Но по определению группы для любого элемента множества имеется симметричный, т.е. в группе для любого элемента обратный к нему – единственный., 3) (a, bG) ax = b, ya = b относительно переменных х, у имеют единственное решение. Д-во: ах = b, х = а-1b, а(а-1b) = (аа-1)b = b. Пусть с – произвольное решение данного уравнения: с =1с = (а-1а)с = а-1(ас) = а-1b. Следовательно, элемент а-1b является единственным решением первого уравнения. Аналогично доказ-ся, что bа-1 является единственным решением второго уравнения. 4) (a, b, сG) ab = ac  b = c. 5) (a, bG) ab = a  b = e, ba = a  b = e. 6) (a, bG) ab = 1  b = a^-1  a = b^-1. 7) Пусть имеются элементы а₁, а₂, а₃, …, а_n. Под произведением трех элементов будем понимать: а₁а₂а₃ = (а₁а₂)а₃; под произведением четырех: а₁а₂а₃а₄ = (а₁а₂а₃)а₄, и т.д. Произведение n элементов – есть произведение след. вида: (а₁а₂…а_n-1)а_n. Под степенью элемента а в группе будем понимать выражение вида: аⁿ =

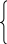1, n = 0,

a, n = 1,

a…a, n > 0,

(a…a)^-1, n < 0.

Если группа с операцией «+», то говорят о кратных элементах: na =

0, n = 0,

a, n = 1,

a + … + a, n > 0,

- (a + … + a), n < 0.

8) Свойства степени: (a, bG) (m, nZ) a^maⁿ = a^m+n; (a^m)^q = a^mq; (ab)ⁿ = aⁿbⁿ. 9) в группе в произведении n элементов скобки можно расставлять любым способом. Непустое подмножество Н группы G называется подгруппой этой группы G, если оно само является группой относительно той же бинарной операции, что и G. Критерий подгруппы (на мультипликативном языке): Пусть нам дано непустое подмножество Н группы G. Н является подгруппой группы G  выполняются след. 2 условия: 1) (a, bH) (ab)H, 2) (aH) a^-1H.

Пусть имеются 2 группы (G₁,), (G₂,). Отображение f: G₁G₂ называется гомоморфизмом групп, если выполняется: (a, bG₁) f(ab) = f(a)f(b). Теорема (о гомоморфном образе группы): гомоморфный образ группы так же является группой относительно своей операции.

Биективным (взаимнооднозначным) отображением называется инъективное и сюрьективное отображение. Отображение f называется инъективным, если: (х₁, х₂Х) х₁  х₂  f(х₁)  f(х₂) или f(х₁) = f(х₂)  х₁ = х₂. Отображение f называется сюрьективным, если: (уY) (xX) f(x) = y. Взаимнооднозначный гомоморфизм называется изоморфизмом.

Непустое множество К называется кольцом, если: 1) (a, bК) (a + b)К. 2) (a, bК) (ab)К. 3) (a, b, cК) (a + b) + c = a +(b + c). 4)(nК) (aK) a + n = n + a = a. 5) (aK) (aК) a + a = a + a = n. 6) (a, bК) a + b = b + a. 7) (a, b, cК) a(bc) = (ab)c. 8) (a, b, cК) a(b + c) = ab + ac, (b + c)a = ba + ca. Свойства колец: 1) 0 – единственный нейтральный элемент относительно «+». 2) (aК) – а является единственным элементом в К. 3) а + х = b имеет единственное решение х = b – a. 4) a + b = a + c  b = c. 5) a + b = a  b = 0. 6) a + b = 0  a = -b  b = -a. 7) –(-a) = a. 8) a0 = 0a = 0 Д-во: а0=а(0+0)=а0 + а0  (по 5 свойству) а0=0.

. 9) (-a)b = -(ab); a(-b) = -(ab); (-a)(-b) = ab. Д-во: (а+(-а))b = 0, (а+(-а))b = ab + (-a)b = 0  (-a)b = -(ab). 10) (a, b, cК) (a - b)c = ac – bc; c(a - b) = ca – cb. Д-во: (a-b)c = (a + (-b))c = ac + (-b)c = ac – bc. Пусть (К, +, ) – кольцо. Подмножество L кольца К называется подкольцом кольца К, если оно является кольцом относительно «+» и «», заданных в К, а К называется надкольцом L. Критерий подкольца: Для того, чтобы непустое подмножество L кольца К было подкольцом кольца К  1) (a, bL)(a + b)L, 2) (a, bL)(ab)L, 3) (aL)-aL. Коммутативное, унитарное кольцо без делителей 0 называют областью целостности. Пусть даны 2 кольца: (К1,+,), (К2,,). Отображение f из кольца К1 в кольцо К2 называется гомоморфизмом, если выполняются след. условия: 1) (a, bK1) f(a+b) = f(a)  f(b), 2) (a, bK1) f(ab) = f(a)  f(b). Теорема: гомоморфный образ кольца является кольцом.

N-множество натур. чисел(1,2,3…). Z-множество цел. чисел(…-1,0,1…).Целое число a делится нацело на b≠0, если  такое qZ, что выполняется a=bq, q-частное, b-делитель, a-делимое.

Свойство отношений делимости. 1. Отношение делимости почти рефлексивно (aZ)(a≠0)(aa). 2. Отношение делимости транзитивно. (ab)(bc)(ac). Д-во: т.к ab qZ, a=bq; bc tZ, b=ct; a=(ct)q=c(tq), tqN ac. 3. Отношение делимости сохраняется при изменение знаков делимого и делителя. ab(-ab)a(-b) (-a)(-b). 4. Если acbc(a±b)c. Д-во: ac qZ, a=cq; bc tZ, b=ct; a±b=cq±ct=c(q±t), (q±t)N. 5. Если acbZ, то abc. 6. Если acbнеc(a±b)неc. Д-во:метод от противного. Представим (a+b)c, тогда qZ, что (a+b)=cq, по условию actZ, что a=ct, ct+b=cq, b=cq-ct=c(q-t), (q-t)Nbc.Пришли к противоречию,bнеc.7. 0 делится на  число b. 8.  число a1. 9. Если а≠0, то не такого целого числа q, что 0q=а. Это свойство исключает деление числа на 0. 0q=0, qZ, поэтому 00 неопределенно однозначно, деление на 0 невозможно. 10. aba≠0|a|>=|b|.Д-во: Пусть abqZ, что a=bq, т.к a≠0, то q≠0 |a|=|bq|, то |q|>=1 |a|=|b||q|1) |q|=1, тогда |a|=|b|, 2) |q|>1, тогда |a|>|b|.

Деление с остатком. Разделить aZ ab, bZ, с остатком, значит найти такие q,rZ, чтобы выполнялись условия 1)a=bq+r,2)0<=r<|b|. Теорема: о деление с остатком. Каковы бы ни были a,bZ, b≠0, всегда возможно и притом ед. образом разделить число a на b с остатком.Д-во: Докажем, что деление a на b с остатком возможно. 1) пусть aZ b>0. Рассмотрим мн-ва всех чисел кратных b, обозначим за Q={…,-3b,-2b,-b,0,b,2b,3b…}. Возьмем число qbQ, чтобы вып-сь след-е условие: qb<=a<b(q+1)(1), qb-qb<=a-qb<b(q+1)-qb, 0<=a-qb<b(2). Обозн. r=a-qb в силу (2), 0<=r<b, а из r=a-qba=qb+rпо опр. ab с остатком. 2)пусть aZ b<0(-b)>0, для этого случая было доказано деление с остатком. Т.о.  (-q),rZ, a=(-b)(-q)+r, 0<=r<(-b)=|-b|, a=bq+r, 0<=r<b. 3)Докажем, единств-ть дел-я с остатком. МОП. Предположим что числа a,bделятся двумя способами. a=bq1+r1,(3), a=bq2+r2,(4), bq1+r1=bq2+r2, bq1-bq2=r2-r1, b(q1-q2)=r2-r1(5), по опр. 0<=r1<|b|, 0<=r2<|b|, 0<=|r2-r1|<|b|, из рав-ва (5) (r2-r1)b, пред-м r2-r1≠0, то по свойству 10, то |r2-r1|>=|b|. Получили r2=r1=r, подставим в рав-ва(3)(4). a=bq1+r, a=bq2+r. bq1+r- bq2-r=0, b(q1-q2)=0, т.к b≠0 q1=q2. НОД. Целое число ≠0 наз-ся ОД а1,а2,…аnZ, если каждое из этих чисел делится на . Целое число d≠0, наз-ся НОД чисел а1,а2,…аnZ, если d-является их ОД, d делится на ОД чисел а1,а2,…аn. Теорема:НОД чисел (а1,а2,…аn)=d определен однозначно с точностью до знака. Если d1,d2-НОД чисел(а1,а2,…аn), то либо d1=d2,d1=-d2. Д-во: Путь d1,d2-НОД чисел(а1,а2,…аn), т.к. d1-НОД, то он делится на  ОД этих чисел, а значит делится и на d2. т.к. d2-НОД, то он делится на  ОД этих чисел, а значит делится и на d1. В силу св-ва отношения делимости d1d2, d2d1 d1=±d2. Алгоритм Евклида: Лемма1: Если число ab, где b>0, a,bZ, то НОД a и b=b. Лемма2: Если число a=bq+r, где b>0, 0<=r<|b|, то НОД a и b=НОД b и r.

Пусть a,bZ, такие что a>b>0, тогда число a делится на b остатком. Возможны 2 случая:1) ab, в силу Леммы 1(a,b)=b. 2) a=bq+r(по Л 2) (a,b)=(b,r), b>r>0. Разделим b на r с остатком:а)br(по Л 1)(b,r)=r(a,b)=r.б)b=rq1+r1(по Л 2)r>r1>0, (b,r)=  (r,r1)(a,b)=(r,r1). Делим r на r1 с ост.: а)rr1 (по Л 1)(r,r1)=r1(a,b)=r1.б)r=r1q2+r2(по Л 2)r1>r2>0, (r,r1)=(r1,r2)(a,b)=(r1,r2). Продолжая этот процесс на каком то шаге мы получим деление без остатка, последний не нулевой остаток будет являться НОД чисел a,b. Теорема: Алгоритм Евклида. Если a=bq0+r1, b=r1q1+r2, r1>r2>=0, r1=r2q2+r3, r2>r3>=0, …, r_m=r_m+1q_m+1+r_m+2, где 0=<r_m<r_m+1, r_m+1=r_m+2q_m+2, то НОД чисел a и b= r_m+2. Д-во: в силу Л 2 мы пол-ем из 1-й строки (a,b)=(b,r1), из 2-й строки (b,r1)=(r1,r2), из 3-й строки (r1,r2)=(r2,r3), из последней строки (r_m,r_m+1)=(r_m+1,r_m+2), В силу Л1 (r_m+1,r_m+2)=(r_m+2). Подставляя эти значения в обратном порядке: (r_m,r_m+1)=r_m+2(a,b)=r_m+2. Св-ва НОД:Т1:Наиб. по величине >0 делитель чисел а1,а2,…аnZ яв-ся НОД этих чисел. Т2: Если каждое из чисел a,b умнож. на одно и тоже число kZ, k≠0, то их НОД умнож. на число k. Т3 Если d-НОД a,b, то  такие x,yZ, что выпол-ся след-е рав-во: ax+by=d-представление НОД чисел a,b в виде их линейной ,комбинации. Д-во: Запишем алгоритм Евклида: a=bq0+r1, b=r1q1+r2, r1=r2q2+r3… r_m=r_m+1q_m+1+r_m+2, r_m+1=r_m+2q_m+2. Из 1-ого рав-ва: r1=a-bq0=x1a+y1b(x1=1, y1=-q0). Из 2-ого рав-ва: r2=b-q1r1=b-q1(x1a+y1b)=x2a+y2b(x2=-q1x1, y2=1-q1y1)…Продолжая анал-е рассуж-я и выкладки мы получим, что r_m+2=x_m+2a+y_m+2b, где x_m+2, y_m+2Z. r_m+2=d, y_m+2=y, x_m+2=xd=xa+yb. НОК. Пусть а1,а2,…аnZ, и они отличны от 0, целое число M наз-ся ОК чисел, если оно делится на каждое из этих чисел. M= а1а2…аn. Целое число m наз-ся НОК чисел а1,а2,…аn, если оно явл-ся их ОК и если  их ОК чисел делится нацело на m. Теорема: Число ab/(a,b) явл-ся НОК чисел a и b. Д-во: пусть (a,b)=da=nd, b=td, где (n,t)-взаймнопростые числа. Рас-м ab/(a,b)=ndtd/d=ndt=at=nb. ab/(a,b)=at(ab/(a,b))a, ab/(a,b)=nb(ab/(a,b))bab/(a,b)-ОК. Пусть M- ОК чисел a и b>0. Покажем, что Мab/(a,b). МaМb. МaSZ, M=aS=ndS, МbKZ, M=bK=tdKndS=tdK nS=tK, tKtnSt, но (n,t)=1StqZ, S=tq, M=ndS=ndtqMndtMab/(a,b). Т.к М-произвольное и Mab/(a,b). Св-ва НОК:1) Если каждое из чисел a и b умножить на одно и тоже число k≠0Z, то НОК этих чисел умнож-ся на k. Д-во: [ka,kb]=kakb/(ka,kb)=k(ab/(a,b))=k[a,b]. 2)если ak и bk, то [a,b] делится на k. 3)Если [a1,a2…an-1]=M и [,an]=m, то [a1,a2…an-1]=m. 4) если [a1,a2]=m1, [m1,a3]=m2, …[mn-2,an]=mn-1, то [a1,a2…an]=mn-1. 5) НОК попарно взаймнопростых чисел (a1,a2…an) равно их произведению. Д-во: (a1,a2…an)-попарно взаймнопростые. (ai,aj)=1, i≠j, i=1…n, j=1…n. По 4-му св-ву m1=[a1,a2]=a1a2/(a1,a2)=a1a2, m2=[m1,a3]= a1a2a3/(a1,a2,a3)=a1a2a3. m_n-1=a1a2…an.