2. Понятие поля, свойства полей. Алгебраические и трансцендентные числа. Структура алгебраических расширений полей. Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексного числа.

Множество Р с алгебраическими операциями «+» и «» называется полем, если для любых элементов выполняются след. условия: 1) (a, b, cР) (a + b) + c = a +(b + c). 2) (a, bР) a + b = b + a. 3)(nР) (aР) a + n = n + a = a. 4) (aР) (aР) a + a = a + a = n. 5) (a, b, cР) a(bc) = (ab)c. 6) (a, bР) ab = ba. 7) (nР) (aР) an = na = a. 8) (aР) (aР) aa = aa = n. 9) (a, b, cP) a(b + c) = ab + ac, (b + c)a = ba + ca. Свойства поля: Справедливы все свойства групп относительно «+» и «» во множестве Р*; все свойства колец, 1) в поле не существует делителей 0. Д-во: МОП Пусть в поле есть делители 0, т.е. а  0 и b  0, аb = 0. Тогда уравнение ах = 0 имеет 2 решения: х = b и х = а. Это противоречит определению поля (т.к. по определению поля ах = b имеет единственное решение а  0). Наше предположение неверно, а верно то, что требовалось доказать. 2) Подмножество Р\{0} – это подмножество ненулевых элементов поля, оно является коммутативной группой относительно «». Из этого свойства получаются такие следствия: а) всякое поле содержит 1 поля, и притом единственную, б) вместе с каждым ненулевым элементом поле Р содержит единственный обратный ему элемент. В поле можно ввести операцию «». Частным элементов а и b поля, где b – ненулевой элемент, будем понимать и обозначать a/b = ab^-1. Символом a/b будем обозначать единственное решение уравнения bx = a. 3) –а = (-1)а. 4)1/ab = (1/a)(1/b) (а  0 и b  0). 5) (b/a)^-1 = a/b (а  0 и b  0). 6) a/b  c/d = (ad  bc)/bd. 7) Критерий равенства дробей: a/b = c/d  ad = bc. Д-во: «»a/b = ab^-1 = cd^-1 / bd  (ab^-1)(bd) = (cd^-1)(bd)  aеd = cеb  ad = cb = bc. «»ad = bc/b^-1d^-1  adb^-1d^-1 = bcb^-1d^-1  ab^-1 = cd^-1  a/b = c/d. 8) (a/b)(c/d) = (ac)/(bd). 9) (a/b) + (-a/b) = 0, -(a/b) = -a/b. Д-во: ab^-1 + (-a)b^-1 = (а + (-а))b^-1 = 0b^-1 = 0. 10) ac = bc  c  0  a = b. 11) ab = 1, то а  0, b = a^-1. 12) ab = 0  a = 0  b = 0. 13) ac/bc = a/b. 14) Пусть в поле Р взяты элементы а, b₁, b₂, b₃, …, b_n, тогда в поле справедлив обобщенный закон дистрибутивности: а(b₁ + b₂ + b₃ + …+ b_n) = аb₁ + аb₂ + аb₃ + …+ аb_n. Пусть дано множество М, которое является подмножеством поля Р (МР). Подмножество М поля Р называется подполем поля Р, если оно само является полем относительно тех же операций, что и в Р. Поле Р называют расширением поля М. Примеры: 1) Q – подполе поля R, 2) А = {a + b2/a, bQ} – подполе поля R. N и Z – не поля, Q – наименьшее поле. Критерий подполя: Для того, чтобы непустое подмножество М поля Р было подполем необходимо и достаточно, чтобы выполнялись условия: 1) (a, bM) a + bM. 2) (a, bM) abM. 3) (aM) -aM. 4) (aM) a^-1M. Теорема: Пересечение подполей является подполем этого поля. Пусть имеется 2 поля (Р₁, +, ) и (Р₂, , ). Отображение f: Р₁Р₂ называется гомоморфизмом, если выполняются след. условия: 1) f(a + b) = f(a)  f(b), 2) f(ab) = f(a)  f(b). Теорема: гомоморфный образ поля является полем. Множество М, содержащее не менее двух чисел, с обычными операциями «+» и «» называется числовым полем, если оно замкнуто относительно действий «+», «-», «», «:». Примеры: Q, R, C, Q[n] = {a + bn/a, bQ}, т.е.  бесконечное множество числовых полей. Теорема( о наименьшем числовом поле): наименьшее числовое поле есть поле рациональных чисел, т.е. любое числовое поле содержит в себе в качестве подполя поле рациональных чисел.

Алгебраические числа. Пусть PF. Число F наз-ся алгеб-м над полем P если  корень не нулевого мн-на из P[x]. -явл-ся числом алгеб-м, т.к. явл-ся корнем x- мн-на. Пример: 2+3=x, 2=x-3, 2=x²-23x+3, 23x=x²+1, 12x²=x⁴+2x²+1, x⁴-10x²+1=0, 2+3-число алгеб-ое над полем Q чисел, т.к. явл-ся корнем ненулевого мн-на с рац-ми коэф-ми. Это минимальный мн-н для которого это число явл-ся корнем.  мнимое число a+bi алгебраично над полем R чисел. F-расширение поля P, -алгеб. число над P. Мн-ен наим. степени принадлежащий P[x] для которого -явл-ся корнем наз-ся минемальным мн-м для . Св-ва миним. мн-в: пусть -алгебр. над P число и мн-н pP[x] миним. для . 1)p-неприводим на полем P. Д-во: пусть p-приводим на полем P. p=p1p2, 1deg p1p, 1deg p2p, т.к. p-миним. мн-н для , то  для него явл-ся корнем. p()=p1()p2()=0, p1()=0p2()=0, -корень мн-а p1.  неможет быть корнем, т.к. степень p1deg p,  неможет быть корнем для p2, т.к. степень p2deg p. 2) 2 миним. мн-на алгеб-о числа  ассоциированы. 3)fP[x]f()=0, p-миним. мн-н для  fp. Д-во: нам надо док-ть что fp, т.е. (p,f)≠1(МОП). Пусть (p,f)=1, тогда по критерию взаимной простоты (Пусть U,VP[x])fU+pV=1, f()U()+p()V()=1, f()=0, p()=00=1, значит наше предположение неверно, а верно то что нужно док-ть. 4)Если неприводимый мн-н qP[x] для которого -корень, то q явл-ся миним. мн-м для . 5)Миним. мн-н алгеб-го числа не может иметь кратных корней. 6)Неприводимый мн-н из P[x] явл-ся миним. для каждого из свойх корней. Степень миним. мн-на для  наз-ся степенью этого числа над полем P. Строение простого расширения. Теорема: Пусть F-расширение поля P, -алгебраична над полем P степени n, тогда простое расширение порожденное эл-ом  есть мн-во. P()={b_n-1^n-1+b_n-2^n-2+…+b₁+b₀/b₀,b₁…b_n-1P}. Д-во: sign: M={b_n-1^n-1+b_n-2 ^n-2+…+b₁+b₀/b₀,b₁…b_n-1P}, покожем что M=P(), т.е M-наименьшее поле содержащее Pи. 1) Покажем что M-поле, т.к. F-поле, и MF, то воспользуемся критерием подполя. 1. ( U,VM)U=b_n-1^n-1+b_n-2^n-2+…+b₁+b₀/b₀,b₁…b_n-1P, V=c_n-1^n-1+c_n-2^n-2+…+c₁+c₀/c₀,c₁…c_n-1P, U+V=(b_n-1+c_n-1)^n-1 +…+(b₁+c₁)+(b₀+c₀), (b_n-1+c_n-1)P и (b₁+c₁)P и (b₀+c₀)P. 2.(UM)(-UM) -U=(-b_n-1)^n-1+(-b_n-2)^n-2 +…+(-b₁)+(-b₀), U+(-U)=0. 3.( U,VM)(UVM) Пусть f-миним. мн-ен для . Степень у него=n. f=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀, по определению миним. мн-на -корень. a_nⁿ+a_n-1^n-1+…+a₁+a₀=0, ⁿ=(-a_n-1/a_n)^n-1+…+(-a₁/a_n)+(a₀/a_n), где (-a_n-1/a_n)P, (-a₁/a_n)P – это число, а значит более высокой степени M. ⁿ⁺¹=ⁿ=(-a_n-1/a_n)ⁿ+…+(-a₁/a_n)²+(a₀/a_n)M. Найдем произведение U,V. UV=(b_n-1^n-1 +…+b₁+b₀)(c_n-1^n-1+…+c₁+c₀)=(b_n-1c_n-1)^2n-2+…+b₀ c₀M, (b_n-1c_n-1),…,b₀c₀P. 4.(U≠0M)(U^-1M) Пусть U=b_n-1^n-1+b_n-2^n-2+…+b₁+b₀, =b_n-1x^n-1+b_n-2x^n-2+…+b₁x+b₀, p-миним. мн-н для элемента , тогда -явл-ся алгебраическим над полем P степени n(усл. теоремы). тогда()≠0, p-неприводим как миним. мн-н(p,)=1 или (p неделится на ). 2-ой случай не возможен, по св-вам(3) миним. мн-ов. Т.к. (p,)=1, то по критерию простоты  такие мн-ны q и hP[x] что выполняется pq+h=1, p()q()+()h()=1, p()=0()=1M/h()M, для () нашелся максим. элемент M, кот-й явл-ся обратным к нему. тогда по критерию M-поле. 2) Покажем что M, PM, число a=0^n-1+…+0+0, aPaM, значит PM, =0^n-1+0^n-2+…++0M. 3). Покажем, что M-миним. из всех полей содержащее  и поле P. Возьмем др. поле L, такое что L, PL и покажем, что ML. (UM)U= b_n-1^n-1+b_n-2^n-2+…+b₁+b₀/b₀,b₁…b_n-1P(PL) b₀,b₁…b_n-1L. L⁰, ¹…^n-1LUL. UM UL. Значит ML, тогда по опр. простого расширения P()=M. Транцендентные расширения. Пусть F-расширение поля P и F, не явл-ся алгебраич. над полем P, тогда элемент  назавем транцендентным над этим полем. Числа транцендентные над полем рац. чисел наз-т транцендентными. Пример: , е. Почти все действительные числа транцендентны. В 1851г. Лиувиль фр. мат-ик док-л теорему, кот. давала способность построения транцендентных чисел. Но этой теоремой нельзя док-ть транцендентность числа е. Она была док-на только в 1873г. учеником Леувиля фр. матем-к Эрмитом. Развивая метод Эрмита в 1882г. нем. мат-к Линдеман док-л транцедентность . В 1874г Кант нашел очень простой способ док-ва сущ-ия транцен-х чисел, более того транцен-х чисел оказалось больше алгебраических.

Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексных чисел.

х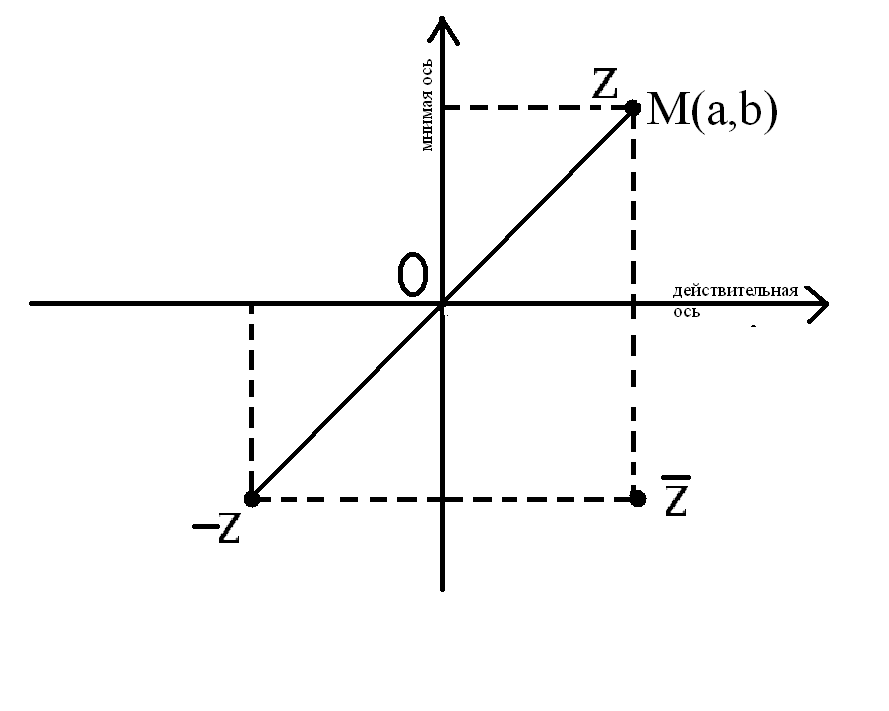 ² + а = 0 – данное уравнение не имеет решений в R при а > 0, в частности неразрешимо уравнение х² + 1 = 0. Можно построить такое расширение поля R, в котором содержится хотя бы 1 элемент, удовлетворяющий уравнению х² + 1 = 0. Будем называть полем комплексных чисел любое поле С, для которого выполняются 3 условия: 1) поле С является расширением поля R. 2) некоторый элемент поля С удовлетворяет уравнению х² + 1 = 0, где 1 и 0 – нейтральные элементы поля относительно «» и «+». 3) всякое подполе поля С, удовлетворяющее условиям 1 и 2, совпадает с полем С. Теорема (о вложении поля R в поле С): Поле R изоморфно полю С. Зададим отображение по правилу а  (а, 0) и (аR) (а, 0) = а. Обозначим i = (0, 1). ii = (0, 1)(0, 1) = (-1, 0) = -1  i² = -1. Пару (a, b) можно представить в таком виде: (a, b) = (a, 0) + (0, b) = a + (0, 1)(b, 0) = a +bi, где а – действительная часть комплексного числа и обозначается ReZ, bi – мнимая часть: ImZ, b – коэффициент мнимой части. а + 0i – действительные числа, 0 + bi – чисто мнимые числа, a +bi – мнимые числа (b  0). Операции над КЧ: 1) a +bi = с +di  a = c  b = d. 2) (a +bi) + (с +di) = (a + c) + (b + d)i. 3) (a +bi) - (с +di) = (a - c) + (b - d)i. 4) (a +bi)(с +di) = (ac - bd) + (ad + bc)i. 5) (a +bi)/(с + di) = ((a +bi)(с - di))/(c² + d²) = ((ac + bd) + (bc - ad)i)/(c² + d²) = ((ac + bd)/(c² + d²)) + ((bc - ad)i)/(c² + d²). Число a – bi называется сопряженным КЧ a + bi и обозначаетсяz. Свойства сопряженных чисел: 1) z +z = 2a. 2) zz = a² + b². 3)(z₁+z₂) =z₁ +z₂. 4)(z₁z₂) =z₁ z₂. 5)(z₁-z₂) =z₁ -z₂. 6)(z₁/z₂) =z₁ /z₂. Число –z называется противоположным числу z: -z = -a – bi. Число 1/z называется обратным для z и обозначается z^-1. Каждому КЧ z поставим в соответствие точку М(a, b) на координатной плоскости.

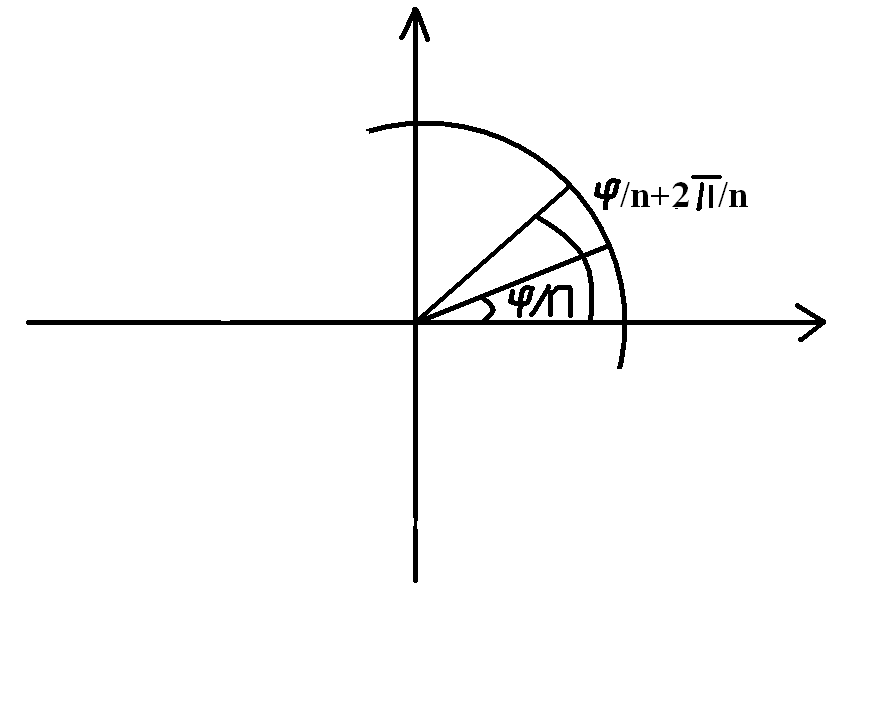
Плоскость получила название комплексной плоскости, а оси – действительной и мнимой. Также геометрической формой КЧ служит радиус-вектор ОМ. Модулем КЧ z = a + bi называется арифметический квадратный корень (а² + b²). |z| = |a + bi| = (а² + b²) = r. Геометрически – это расстояние от т.О до т. М или полярный радиус. Аргументом КЧ z называется действительное число  такое, что: cos = a/r = a/|z|, sin = b/r = b/|z|, и обозначается argz. Теорема (о представлении КЧ z  0 в тригонометрической форме): Каждое КЧ z  0 можно представить в виде z = r(cos + isin), где r,R, r > 0,  = argz. Выражение КЧ z в таком виде называется тригонометрической формой КЧ. Замечание: т.к. аргумент z определен с точностью до 2k, то КЧ z можно представить в тригонометрической форме различными способами: z = r(cos( +2k) + isin( + 2k)). Наименьший по абсолютной величине аргумент называется главным аргументом. Теорема: пусть z₁ = r₁(cos₁ + isin₁), z₂ = r₂(cos₂ + isin₂), z₁  0, z₂  0. Тогда z₁z₂ = r₁r₂(cos(₁ + ₂) + isin(₁ + ₂), z₁/z₂ = r₁/r₂(cos(₁ - ₂) + isin(₁ - ₂). Из этой теоремы можно привести равенство: |z₁z₂| = |z₁||z₂| = r₁r₂, arg(z₁z₂) = argz₁ + argz₂ и |z₁/z₂| = |z₁|/|z₂| = r₁/r₂, arg(z₁/z₂) = argz₁ - argz₂. Степенью КЧ z называется: 1) zⁿ = zz…z, nN, n > 1, 2) z⁰ = 1, z  0, 3) z¹ = z, 4) z^-n = (z^-1)ⁿ = (1/z)ⁿ, nN. Свойства степени: 1) (z₁z₂)ⁿ = z₁ⁿz₂ⁿ, 2) i^4q+r = i^r. Если n – простое число, то iⁿ = i. Теорема(о степени КЧ в тригонометрической форме): при возведении КЧ в степень модуль КЧ возводится в эту степень, аргумент КЧ умножается на показатель степени: zⁿ = |z|ⁿ(cosn + isinn) – это формула Муавра. Частный случай: (cos + isin)ⁿ = cosn + isinn, если модуль КЧ = 1. Д-во: по определению: 1) пусть n = 0, z⁰ = 1, |z|⁰(cos0 + isin0) = 1. 2) n = 1, z¹ = z, |z|¹(cos + isin) = z. 3) для д-ва истинности формулы Муавра для любого натурального числа n воспользуемся ММИ: 1) n = 1 (доказано), 2) пусть формула Муавра выполняется для r = k, т.е. z^k = |z|^k(cosk + isink) (*), и докажем для n = k + 1, т.е. нужно доказать, что выполняется: z^k+1 = |z|^k+1(cos(k+1) + isin(k+1)). Умножим обе части равенства (*) на z: z^kz = |z|^k(cosk + isink)|z|(cos + isin) = |z|^k+1(coskcos + coskisin + isinkcos - sinksin) = |z|^k+1((coskcos - sinksin)+(cosksin + sinkcos)i) = |z|^k+1(cos(k+1) + isin(k+1)). Значит, формула верна для любого nN. 4) Докажем для n < 0, nN: zⁿ = 1/z^-n = 1/(|z|^-n(cos(-n) + isin(-n))) = (|z|ⁿ(cosn + isinn))/((cosn + isinn)(cosn - isinn)) = (|z|ⁿ(cosn + isinn))/((cosn)² + (sinn)²) = |z|ⁿ(cosn + isinn). Если |z| = 1, zⁿ = 1ⁿ(cosn + isinn) = cosn + isinn; (cosn + isinn)ⁿ = cosn + isinn. Эта теорема позволяет находить формулы для cos и sin кратного угла. Читд. КЧ u называется корнем n-ной степени из КЧ z, если uⁿ = z, nN, n2. u = ⁿz. Теорема (о корне n-ной степени из КЧ): Корень n-ной (nN, n2) степени из КЧ z  0 имеет ровно n значений. Если z задана в тригонометрической форме, то все значения корня n-ной степени из z будут числа: u_k = ⁿr (cos((+2k)/n) + isin((+2k)/n)), k = 0, …, n-1; uⁿ = z, nN, n2, u = ⁿz. Из формулы извлечения корня следует: 1) т.к. модуль всех КЧ – есть число постоянное, то все корни u_k лежат на окружности с центром в точке (0, 0) и радиусом ⁿr; 2) argu^k = (+2k)/n, k = 0, …, n-1; argu₁ = /n, argu₂ = /n + 2/n. Аргумент всех u_k отличается на 2/n, а т.к. этих аргументов ровно n, то все корни лежат в вершинах правильного n-угольника.

Следствие 1: пусть v – любое значение корня n-ной степени из z₁: vⁿ = z₁, v = ⁿz₁, z₁  0. u₀, u₁, u₂, …, u_n-1 – все n значений (различных) из КЧ z₂, где z₂  0. Тогда ⁿz₁z₂ = {vu₀, vu₁, vu₂, …, vu_n-1}. Следствие 2: если u₀, u₁, u₂, …, u_n-1 – все значения ⁿz, z  0, тоu₀,u₁,u₂, …,u_n-1 – все значения ⁿz. Пусть n – любое натуральное число, отличное от 0. Корнем n-ной степени из 1 называется такое КЧ _k, n-ная степень которого = 1: _k = ⁿ1. Число , являющееся значением корня n-ной степени из 1, называется первообразным корнем n-ной степени из 1, если степени его: ⁰ = 1; ¹ = ; …; ^n-1 – различны между собой, что означает, что они являются всеми значениями корня n-ной степени из 1.