
- •Группы, кольца. Примеры, основные свойства. Кольцо целых чисел. Теорема о делении с остатком. Наибольший общий делитель и наименьшее общее кратное.
- •Понятие поля, свойства полей. Алгебраические и трансцендентные числа. Структура алгебраических расширений полей. Поле комплексных чисел. Формула Муавра. Извлечение корня из комплексного числа.
- •Кольцо многочленов над полем. Приводимые и неприводимые над полем многочлены. Теорема о разложении многочлена в произведение неприводимых множителей(доказательство)
- •Определители и их свойства. Основные методы вычисления определителей. Системы линейных уравнений. Разрешимость систем линейных уравнений. Методы решения.
- •Кольцо целых чисел. Отношение делимости. Простые числа. Бесконечность множества простых чисел. Основная теорема арифметики.
- •Числовые сравнения и их свойства. Теоремы Эйлера и Ферма. Линейные сравнения с одним неизвестным. Методы решения.
- •Линейные операторы. Собственные векторы и собственные значения линейного оператора, их свойства и отыскание.
Линейные операторы. Собственные векторы и собственные значения линейного оператора, их свойства и отыскание.
Линейное отображение векторного пространства pV в себя называется линейным оператором, т.е. линейный оператор – это гомоморфизм векторного пространства V в себя. Пример: рассмотрим векторное пространство QR2 и рассмотрим : R2R2. (a, b) (2a, 2b). Свойства линейного оператора: Т.к. линейный оператор – это гомоморфизм, то выполняются все свойства гомоморфизма (() = , (-а) = -(а), линейно зависимая система переходит в линейно зависимую систему, образ линейной комбинации является линейной комбинацией образов с теми же коэффициентами). Частный случай линейного оператора: 1) пусть pV – векторное пространство и отображение : VV – задано по правилу: (х) = х. Данное отображение является линейным оператором. Этот оператор называют тождественным или единичным. 2) пусть pV – векторное пространство и - фиксированный элемент поля Р. Отображение : VV – задано по правилу: (х) = х. Данное отображение является линейным оператором. Этот оператор называют оператором гомотетией с коэффициентом . Оператор гомотетии с коэффициентом = 0 называется нулевым оператором. Оператор гомотетии коэффициентом = 1 – есть оператор тождественный или единичный. 3) пусть L1 и L2 – подпространства пространства V, причем V = L1 L2. (хV) (!lL1) (!uL2) х = l + u. Рассмотрим : VV, которое каждому вектору х ставит в соответствие его компоненту lL1: хlL1. По свойствам подпространств - линейный оператор и его называют оператором проектирования. 4) пусть RF – векторное пространство действительных функций одной переменной х, определенных и неограниченно дифференцируемых на множестве R. Оператор D: FF, ставящий в соответствие каждому элементу из F его производную, является линейным оператором. (fF) D(f) = f = df/dx; D(f + g) = D(f) + D(g); (f + g) = f +g; D(f) = D(f); f = f , где R. Этот оператор называется оператором дифференцирования. Теорема: пусть pV – векторное пространство и (е1, е2, …, еn) – базис. Возьмем произвольную систему векторов: а1, а2, …, аn пространства V. Тогда ! Линейное отображение (еi) = аi, i = 1, …, n. Замечание: аналогичная теорема справедлива и для двух различных пространств. Множество векторов линейного пространства V, которое под действием линейного оператора переходит в , называется ядром линейного оператора и обозначается Ker: Ker = {aV/(a) = }. Т.е. ядро линейного оператора – это полный прообраз нулевого вектора при отображении : Ker = -1. Т.к. ядро линейного оператора – подпространство, то для конечномерного пространства V есть смысл говорить о размерности ядра линейного оператора. Размерность ядра линейного оператора называется дефектом линейного оператора и обозначается: dimKer (или d). Образом линейного оператора называется множество всех векторов образа линейного оператора: (V) = {bV/(aV) (a) = b} и обозначается: Im. Размерность образа линейного оператора называется рангом линейного оператора и обозначается: r() = dimIm. Теорема (о связи размерности векторного пространства с рангом и дефектом линейного оператора): Пусть - линейный оператор конечномерного векторного пространства pV. Сумма ранга и дефекта линейного оператора = размерности пространства V.
Пусть pV – конечномерное векторное пространство. (1) е1, е2, …, еn – базис пространства V. - линейный оператор пространства V. Представим векторы (е1), (е2), …, (еn) в виде линейной комбинаций базиса (1): (е1) = 11е1 + 21е2 + …+ n1еn, (е2) = 12е1 + 22е2 + …+ n2еn, …, (еn) = 1nе1 + 2nе2 + …+ nnеn. Матрица

 11, 21,
…, n1
11, 21,
…, n1
М() = 12, 22, …,n2 ,
………………………..
1n, 2n, …,nn
k-тый столбец которой есть координатный столбец вектора (еk) относительно базиса (1) называется матрицей линейного оператора относительно базиса (1). Каждому линейному оператору в заданном базисе соответствует матрица. В силу теоремы о задании линейного оператора с помощью отображения базиса справедлива и обратная: какова бы ни была квадратная матрица, ей соответствует некоторый линейный оператор n-мерного линейного пространства. Действия над линейными операторами: 1) Суммой ЛО f и будем называть отображение, определяемое формулой: (f + )(а) = f(а) + (а). Теорема: сумма ЛО пространства V есть ЛО этого пространства. 2)Если - ЛО конечномерного векторного пространства и Р, то будем называть отображение, определяемое формулой: ()(а) = (а). 3) Пусть f и - ЛО пространства V, произведением этих ЛО называется отображение, ставящее в соответствие элементу а из V: а(f(а)). (f)(a) = (f(a)) = f((a)).
Ненулевой вектор ЛО в рV называется собственным вектором ЛО , если такой скаляр , что (а) = а. Число при этом называют собственным значением вектора. Пример: (х, у)(2х, 2у). Свойства СВ и СЗ: 1)СВ ЛО имеет ! СЗ относительно одного и того же ЛО. Д-во: МОП Пусть СВа имеет 2 СЗ 1 и 2. (а) = 1а, (а) = 2а. Тогда в силу однозначности оператора : 1а = 2а. а(1 - 2) = . 1 - 2 = 0, 1 = 2. 2) Если а1, а2, …, аr – это линейно независимая система СВ ЛО с одним и тем же СЗ , то любая линейная комбинация этих векторов, в которой хотя бы один коэффициент 0, является СВ с тем же СЗ . Д-во: рассмотрим вектор а = 1а1 + 2а2 + …+ rar, где iР, I . Находим (а) = (1а1 + 2а2 + …+ rar) = (1а1) + (2а2) + …+ (rar) = 1(а1) + 2(а2) + …+ r(ar) = 1а1 + 2а2 + …+ rar = а. 3) Все СВ ЛО конечномерного пространства V, имеющие одно и то же СЗ, вместе с образуют линейное пространство. Это подпространство называют собственным подпространством пространства V. Теорема: пусть - ЛО и Р и - СЗ этого оператора. Множество всех СВ с СЗ относительно совпадает с множеством Ker( - )\{0}. Теорема: пусть - ЛО векторного пространства Vn и относительно базиса е1, е2, …, еn. Матрица этого оператора М() и число являются СЗ ЛО , тогда определитель: |М() - Е| = 0 (1). Уравнение (1) с переменной называют характеристическим уравнением матрицы М() ЛО . Т.о. задача по отысканию СВ ЛО сводится к след. алгоритму: 1) зная М(), составить характеристическое уравнение и решить его относительно переменной . 2) найденные значения 1, 2, …, n подставить в систему, полученную из характеристического уравнения и определить вектор а = (1, 2, …, n). Теорема: Если квадратные матрицы А и В подобны, то их характеристические уравнения совпадают. Следствие: характеристические уравнения матриц ЛО относительно различных базисов совпадают. Т.о. можно говорить о характеристическом уравнении ЛО, не указывая базис
Корни многочлена. Методы нахождения корней. Результант многочленов, его связь с корнями. Многочлены от нескольких переменных над полем. Симметрические многочлены. Основная теорема о симметрических многочленах.
Пусть f – произвольный многочлен из кольца А[x]. Пусть с – элемент из области целостности А. Сумму ancn + an-1cn-1 + … + a1c + a0 ,будем называть значением многочлена f и обозначать: f(c). Константа с называется корнем многочлена f, если f(c) = 0. Теорема Безу: пусть fА[x] и сА, тогда в кольце А[x] многочлен Q такое, что f = (x - c)q + f(c). Другая формулировка: остаток от деления многочлена f на двучлен х – с равен значению многочлена f от константу с. Теорема (критерий корня): Константа с является корнем многочлена f f двучлен (х - с). Д-во: Необходимость: пусть f – многочлен, для которого с – корень. Докажем, что f(х - с). По теореме Безу f = (x - c)q + f(c) = (x - c)q. Достаточность: f(x - c). Д-ть: с – корень. f(x - c) f = (x - c)q, f(c) = (c - c)q = 0. Читд. Схема Горнера – это аппарат, который позволяет найти результат от деления многочлена f на двучлен х – с. Пример: выполнить деление по схеме Горнера f(x) = 3x4 – 2x3 +5 на (х + 2):
3 -2 0 0 5
-2 3 -8 16 -32 69
3x4 – 2x3 +5 = (х + 2)(3x3 -8х2 + 16х - 32) + 69.
fА[x], f 0, сА. Если с – корень многочлена f, то по критерию корня это означает, что f(x - c) f = (x - c)q. Если с – корень многочлена q, то q = (x - c)h, f = (x - c)2h, …. Может оказаться, что с – корень многочлена h и т.д. Наибольшая натуральная степень двучлена х – с, на которую делится многочлен f, называется порядком кратности корня с для многочлена f. Т.о. с является k-кратным корнем многочлена f f (x - c)k f не делится на (x - c)k+1. Константа с есть k-кратный корень многочлена f, если f = (x - c)k, не делится на (x - c). Теорема: если многочлен f = anxn + an-1xn-1 + … + a1x + a0Z[x] имеет несократимую дробь p/q корнем, то: 1) р – делитель а0, а q – делитель аn. 2) p – mq – делитель f(m) для mZ. Следствие: Если p/q – корень, то f(1)(p - q), a f(-1)(p + q). Замечание: данная теорема является лишь необходимым условием существования корня, а поэтому с помощью 1 условия можно найти все возможные корни, с помощью 2 условия можно отбросить некоторые, но в конечном итоге все они должны быть проведены по схеме Горнера. Пример: Найти рац. корни многочлена 4х3 – 3х -1. р = {1}, q = {1, 2, 4}. p/q = {1, ½, ¼}. f(1) = 0. f(-1) = -2.
корни |
½ |
-½ |
¼ |
-¼ |
(-2/(p + q))Z |
- |
+ |
- |
- |
4 0 -3 -1
-½ 4 -2 -2 0
-½ 4 -4 0
-½ 4 -6
Ответ: данный многочлен имеет 2 рац. корня: простой корень -1 и двукратный корень -½.
Уравнением 3 степени называется уравнение вида: а3х3 + а2х2 + а1х + а0 = 0 (1), где а0, а1, а2, а3С, а3 0. Комплексное число называется корнем этого уравнения, если а33 + а22 + а1 + а0 = 0. Преобразуем (1): х3 + а2х2/а3+ а1х/а3 + а0/а3 = 0 (2). Уравнения (1) и (2) равносильны. (2): х3 + ах2 + bх + c = 0. Делаем подстановку: х = у – а/3. (у – а/3)3 + а(у – а/3)2 + b(у – а/3) + c = 0. Получим уравнение: у3 + у(-а2/3 + b) + (-a3/27 + a3/9 – ab/3 + c) = 0. (3): у3 + ру + q = 0. Такое уравнение называется приведенным кубическим уравнением. Пусть имеется уравнение (*):х3 + рх + q = 0. Будем искать корни этого уравнения в виде х = + . ( + )3 + р( + ) + q = 0; 3 + 3 + ( + )(3 + p) + q = 0. Потребуем, чтобы выполнялось условие: 3 + p = 0 = -р/3. Тогда 3 + 3 = -q.
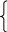
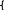
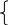 3 + 3
= -q,
3 + 3
= -q,
3 + 3
= -q,
3 + 3
= -q,
= -р/3. 33 = -р3/27.
С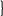 огласно
формулам Виета 3
и 3 – есть
корни квадратного уравнения: u2
+ qu - р3/27. Это уравнение
называется разрешающим для уравнения
(*). D = q2
+ 4p3/27; u1,2
= (-q
(q2
+ 4p3/27))/2;
= 3(-q/2
+ (q2/4
+ p3/27)).
= 3(-q/2
- (q2/4
+ p3/27)). Это формулы
Кардана. Следствие: Корни уравнения (*)
выражаются след. формулами: х1 =
+ ; х2 = -(
+ )/2 + i3(
- )/2; x3
= - ( + )/2
- i3(
- )/2. Замечание:
1)Если >0, то уравнение
имеет 1 действительный корень и 2 мнимых
сопряженных, 2) Если =0,
то уравнение имеет действительные
корни и хотя бы 1 из них – кратный, 3) Если
<0, то все корни
уравнения действительные и различны.
Уравнением 4 степени называют одномерный
предикат с переменной х такого вида:
а4х4 + а3х3 + а2х2
+ а1х + а0 = 0 (1), а4
0. Разделим на а4: х4 + ах3
+ bх2 + cх
+ d = 0. Метод Феррари: 1 ШАГ:
х4 + ах3 = -bх2
- cх - d = 0. 2
ШАГ: Дополним левую часть до полного
квадрата: (х2)2 + 2х2·½х
+ а2х2/4 = а2х2/4 –
bx2 – cx
– d; (x2
+ ½ax)2 = а2х2/4
- bx2 – cx
– d. 3 ШАГ: снова дополним
левую часть до полного квадрата, добавляя
слагаемое с новой переменной у: (x2
+ ½ax)2 + 2(x2
+ ½ax)у + у2 = 2(x2
+ ½ax)у + у2 + а2х2/4
- bx2 – сх – d,
(х2 + ах/2 + y)2 =
x2(2y
+ a2/4 - b)
+ (ay - c)x
+ (y2 - d)
(*). Поскольку в левой части полный
квадрат, то это уравнение имеет двукратный
корень. А это возможно, когда у уравнения
в правой части дискриминант = 0. Найдем:
D = (ay - c)2
– 4(2y + a2/4
- b)(y2
- d) = 0. Найдем некоторый
корень кубического уравнения относительно
у. Пусть это число у1. Подставим
его в уравнение (*). В правой части
подчеркнутого уравнения появится полный
квадрат, т.е. правая часть уравнения
примет вид: (х2 + ах/2 + y1)2
= (sx + v)2.
Последнее уравнение преобразуется в
дизъюнкцию двух уравнений: х2 +
ах/2 + y1 = sx
+ v
х2 + ах/2 + y1 =
-sx – v. 4 ШАГ:
Решим полученные уравнения. Пусть f
и g – это многочлены кольца
Р[х]. Найдем условие, при котором эти
полиномы обладают общим делителем
положительной степени. Теорема: пусть
f – полином: f
= a0xn
+ a1xn-1
+ …+ an
и многочлен g = b0xm
+ b1xm-1
+ …+ bn.
И по крайней мере 1 из коэффициентов а0,
b0 отличен от 0.
Полиномы f и g
имеют общий делитель положительной
степени в кольце Р[х]
в Р[х] полиномы с и
dР[х],
удовлетворяющие условиям: 1) fc
= gd, 2) c =
c0xm-1
+ c1xm-2
+ …+ cm-1,
d = d0xn-1
+ d1xn-2
+ …+ dn-1,
3) хотя бы 1 из полиномов с или d
отличен от 0. Запишем условия 1 и 2 более
подробно: 1) (a0xn
+ a1xn-1
+ …+ an)(c0xm-1
+ c1xm-2
+ …+ cm-1)
= (b0xm
+ b1xm-1
+ …+ bn)(d0xn-1
+ d1xn-2
+ …+ dn-1).
Произведем умножение в обеих частях
равенства и приравняем коэффициенты
при одинаковых степенях переменной х,
получим след. систему линейных уравнений:
a0c0
= b0d0;
a1c0
+ a0c1
= b1d0
+ b0d1;
a2c0
+ a1c1
+ a0c2
= b2d0
+ b1d1
+ b0d2;
…; ancm-2
+ an-1cm-1
= bmdn-2
+ bm-1dn-1;
ancm-1
= bmdn-1.
Это есть система n+m
однородных линейных уравнений с
переменными c0, c1,
…, cm-1,
d0, d1,
…, dn-1.
Она имеет ненулевые решения
определитель этой системы = 0. Для того,
чтобы избежать появления минусов перед
элементами матрицы определителя, можно
перенеся правые части уравнений влево.
Будем считать переменными c0,
c1, …, cm-1,
-d0, -d1,
…, -dn-1.
Кроме того транспонируем матрицу
определителя, тогда определитель примет
вид: R =
огласно
формулам Виета 3
и 3 – есть
корни квадратного уравнения: u2
+ qu - р3/27. Это уравнение
называется разрешающим для уравнения
(*). D = q2
+ 4p3/27; u1,2
= (-q
(q2
+ 4p3/27))/2;
= 3(-q/2
+ (q2/4
+ p3/27)).
= 3(-q/2
- (q2/4
+ p3/27)). Это формулы
Кардана. Следствие: Корни уравнения (*)
выражаются след. формулами: х1 =
+ ; х2 = -(
+ )/2 + i3(
- )/2; x3
= - ( + )/2
- i3(
- )/2. Замечание:
1)Если >0, то уравнение
имеет 1 действительный корень и 2 мнимых
сопряженных, 2) Если =0,
то уравнение имеет действительные
корни и хотя бы 1 из них – кратный, 3) Если
<0, то все корни
уравнения действительные и различны.
Уравнением 4 степени называют одномерный
предикат с переменной х такого вида:
а4х4 + а3х3 + а2х2
+ а1х + а0 = 0 (1), а4
0. Разделим на а4: х4 + ах3
+ bх2 + cх
+ d = 0. Метод Феррари: 1 ШАГ:
х4 + ах3 = -bх2
- cх - d = 0. 2
ШАГ: Дополним левую часть до полного
квадрата: (х2)2 + 2х2·½х
+ а2х2/4 = а2х2/4 –
bx2 – cx
– d; (x2
+ ½ax)2 = а2х2/4
- bx2 – cx
– d. 3 ШАГ: снова дополним
левую часть до полного квадрата, добавляя
слагаемое с новой переменной у: (x2
+ ½ax)2 + 2(x2
+ ½ax)у + у2 = 2(x2
+ ½ax)у + у2 + а2х2/4
- bx2 – сх – d,
(х2 + ах/2 + y)2 =
x2(2y
+ a2/4 - b)
+ (ay - c)x
+ (y2 - d)
(*). Поскольку в левой части полный
квадрат, то это уравнение имеет двукратный
корень. А это возможно, когда у уравнения
в правой части дискриминант = 0. Найдем:
D = (ay - c)2
– 4(2y + a2/4
- b)(y2
- d) = 0. Найдем некоторый
корень кубического уравнения относительно
у. Пусть это число у1. Подставим
его в уравнение (*). В правой части
подчеркнутого уравнения появится полный
квадрат, т.е. правая часть уравнения
примет вид: (х2 + ах/2 + y1)2
= (sx + v)2.
Последнее уравнение преобразуется в
дизъюнкцию двух уравнений: х2 +
ах/2 + y1 = sx
+ v
х2 + ах/2 + y1 =
-sx – v. 4 ШАГ:
Решим полученные уравнения. Пусть f
и g – это многочлены кольца
Р[х]. Найдем условие, при котором эти
полиномы обладают общим делителем
положительной степени. Теорема: пусть
f – полином: f
= a0xn
+ a1xn-1
+ …+ an
и многочлен g = b0xm
+ b1xm-1
+ …+ bn.
И по крайней мере 1 из коэффициентов а0,
b0 отличен от 0.
Полиномы f и g
имеют общий делитель положительной
степени в кольце Р[х]
в Р[х] полиномы с и
dР[х],
удовлетворяющие условиям: 1) fc
= gd, 2) c =
c0xm-1
+ c1xm-2
+ …+ cm-1,
d = d0xn-1
+ d1xn-2
+ …+ dn-1,
3) хотя бы 1 из полиномов с или d
отличен от 0. Запишем условия 1 и 2 более
подробно: 1) (a0xn
+ a1xn-1
+ …+ an)(c0xm-1
+ c1xm-2
+ …+ cm-1)
= (b0xm
+ b1xm-1
+ …+ bn)(d0xn-1
+ d1xn-2
+ …+ dn-1).
Произведем умножение в обеих частях
равенства и приравняем коэффициенты
при одинаковых степенях переменной х,
получим след. систему линейных уравнений:
a0c0
= b0d0;
a1c0
+ a0c1
= b1d0
+ b0d1;
a2c0
+ a1c1
+ a0c2
= b2d0
+ b1d1
+ b0d2;
…; ancm-2
+ an-1cm-1
= bmdn-2
+ bm-1dn-1;
ancm-1
= bmdn-1.
Это есть система n+m
однородных линейных уравнений с
переменными c0, c1,
…, cm-1,
d0, d1,
…, dn-1.
Она имеет ненулевые решения
определитель этой системы = 0. Для того,
чтобы избежать появления минусов перед
элементами матрицы определителя, можно
перенеся правые части уравнений влево.
Будем считать переменными c0,
c1, …, cm-1,
-d0, -d1,
…, -dn-1.
Кроме того транспонируем матрицу
определителя, тогда определитель примет
вид: R =


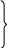 a0
a1
a2 …
an
…
a0
a1
a2 …
an
…
a0 a1 a2 … an … m
a0 a1 a2 … an …
……………………………

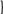 b0
b1
b2 …
bm …
b0
b1
b2 …
bm …
b0 b1 b2 … bm … n
b0 b1 b2 … bm …
……………………………
Результантом полиномов f и g называется определитель R. Полиномы f и g, у которого а0 0 или b0 0, имеют общий делитель положительной степени система линейных уравнений имеет ненулевые решения, т.е. когда определитель R = 0. Следствие: Если результант полиномов f и g = 0, то либо полиномы имеют общий делитель положительной степени, либо коэффициенты а0, b0 равны 0 и обратно. Пример: вычислить результант полиномов: f(x) = x3 – 3x2 + 2x + 1; g(x) = 2x2 – x – 1. R(f, g) = 1 -3 2 1 0 2 = 1 -3 2 1 0 = (-1)7· 1 -3 2 1


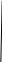
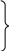 0 1 -3 2 1
0 1 -3 2 1 2 -1 -1
0
0 1 -3 2 1
0 1 -3 2 1 2 -1 -1
0
 2 -1 -1 0 0 2 -1 -1 0 0
0 2 -1 -1
2 -1 -1 0 0 2 -1 -1 0 0
0 2 -1 -1
0 2 -1 -1 0 0 2 -1 -1 0 0 1 -1 1
0 0 2 -1 -1 0 1 -1 1 0
= … = -7. Ответ: не имеет общих делителей положительной степени.
Пусть имеется система уравнений, обозначим ее:
 f(x, y)
= 0,
f(x, y)
= 0,
g(x, y) = 0.
Запишем каждое из уравнений f и g по убывающим степеням переменной. f(x, y) = an(y)xn + an-1(y)xn-1 +…+ a1(y)x + a0(y); g(x, y) = bm(y)xm + bm-1(y)xm-1 +…+ b1(y)x + b0(y). ai(y), bi(y) – многочлены над полем Р от переменной у. Найдем результант полиномов f и g – R(y). Если результант R(y) = 0, то уравнение есть результат исключения переменной х из системы уравнений.
Многочлены от нескольких переменных. Симметрические многочлены Пусть имеется некоторая область целостности А(область целостности К называется кольцом главных идеалов, если этого кольца является главным). Рассмотрим кольцо многочленов от 1-ой переменной х1 над областью целостности А, т.е. A[x1], тогда элементы кольца можно представить в следующем виде: а1*х1n +…+ ai*x1+a0, aiA. Знаем, что кольцо А[x1] является областью целостности, значит можно рассмотреть кольцо многочленов от 1-ой переменной х2 над областью целостности А[x1]. Тогда получим следующее (A[x1])[x2]=A[x1,x2]={bn*x2n+bn-1*x2n-1+…+bi*x2+b0 |biA[x1]}={ai1*ai2*x1i1*x2i2 |ai1i2A}. Тогда кольцо A[x1,x2] также является областью целостности, а значит можно рассматривать кольцо многочленов от 1-ой переменной х3 над областью целостности A[x1,x2]. Получим: A[x1,….,xn]. Его элементы можно представить следующим образом: ai1 i2…in* x1i1*x2i2…xnin | ai1 i2…inA, каждое слагаемое в этой записи называется одночленом. Степенью одночлена называется сумма показателей переменных, входящих в этот одночлен, т.е. i1+…+in. Степенью многочлена будем называть наибольшую из степеней одночлена, входящих в этот многочлен. Однородным многочленом называется многочлен все одночлены которого имеют одинаковую степень. Утверждение любые многочлены, м. представлять в виде суммы однородных многочленов. Лексика графическая запись: Пусть имеется два одночлена: =a*x1i1*x2i2*…*xnin ; =b*x1k1*x2k2*…*xnkn Будем говорить, что одночлен выше одночлена , если такой номер s, что i1=k1,…,is-1=ks-1; is>k1. Обозначения: . Th: Отношение «выше» на множестве одночленов является отношением транзитивности. Данная теорема говорит, что каждый последующий не выше предыдущего. Такую запись многочлена называют лексико графической записью. Первый одночлен многочлена называется высшим членом многочлена, др. словами этот одночлен выше др. одночленов данного многочлена. Th: (о высшем члене произведения многочлена) высший член произведения двух многочленов равен произведению высших членов сомножителей. Многочлен называется симметрическим если он не изменяется при любой биективной замене переменных. Среди всех симметрических многочленов выделяют основные элементарные симметрические многочлены: 1(x1…xn)=x1+…+xn 2(x1…xn)=x1*x2+x1*x3+…+x1*xn+x2*x3+…+xn-1*xn
3(x1…xn)= x1*x2*x3+…+xn-2* xn-1*xn
n(x1…xn)= x1*x2*…*xn
Лемма1: Пусть имеется симметрический многочлен f и =a*x11*x22*…*xnn – его высший член, тогда 1 2 …n
Лемма2: Пусть имеется симметрический многочлен f и =a*x11*x22*…*xnn –его высший член, тогда многочлен g=a*11-2*22-3*…*n-1(n-1)-n*nn имеет тоже высший член при переходе от x
Теорема:
Любой симметрический многочлен от n
неизвестных можно представить в виде
многочлена от 1*
2*…*n
(т.е. осуществлять переход от x
) и такое
представление ! с точностью до порядка
следования сомножителей и слагаемых.
Алгоритм записи симметрического многочлена отi:
1. представить данный многочлен в виде суммы однородных многочленов
2. для каждого однородного слагаемого осуществить переход от x следующим образом:
а) определить высший член этого многочлена
б) выписать систему показателей этого высшего члена
3. построить систему показателей так, чтобы каждая система соответствовала бы более низшему одночлену, а в сумме системы показатели равнялись
4. для каждой выписанной системы показателей составить многочлен от по правилу Леммы2.
5. методом неопределенных коэффициентов найти коэффициент при переходе от x
