
- •4.Условия выпуклости графика функции. Точки перегиба.
- •5.Асимптоты графика функции
- •6.Общая схема исследования функции и построения графика
- •3.Глобальный экстремум на отрезке
- •2.Локальные экстремумы. Необходимое и достаточные условия существования экстремума
- •7.Определение функции нескольких переменных. Способы задания ф.Н.П.
- •9.Предел функции в точке, непрерывность ф.М.П.
- •14.Локальные экстремумы ф.М.П.
- •15. Необходимое условие существования экстремума
- •16. Достаточные условия существования экстремума
- •1.Исследование функции на монотонность
- •36.Решение ду 1-го порядка с разделяющимися переменными.
- •11. Дифференцируемость ф.М.П. Примеры применения частных производных в экономике.
- •19. Наибольшее и наименьшее значения ф.М.П. В ограниченной замкнутой области.
- •26. Услов интегрируемости функ. Форм. Нюьтона-Лейбница
- •27. Свойства определенного интеграла
- •28.Геометрические приложения определенного интеграла
4.Условия выпуклости графика функции. Точки перегиба.
График дифференцируемой функции y=f(x) называется выпуклым вниз на интервале (а;Ь),если он расположен выше любой ее касательной на этом интервале. График функции у=f(x) называется выпуклым вверх на интервале (а; Ь), если он расположен ниже любой ее касательной на этом интервале.Точка графика непрерывной функции у= f(x), отделяющая его части разной выпуклости, называется точкой перегиба.
Интервалы
выпуклости вниз и вверх находят с помощью
следующей теоремы:Если
функция
у=f(x)
во всех точках интервала (а;Ь)
имеет отрицательную вторую производную,
т. е.
f"(x)
< 0,
то график функции в этом интервале
выпуклый вверх. Если же
f"(x)
> 0
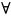 x
x
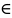 (а;
Ь) —
график выпуклый вниз.
(а;
Ь) —
график выпуклый вниз.
Для нахождения точек перегиба графика функции используется следующая теорема(достаточное условие существования точек перегиба):Если вторая производная f"(x) при переходе через точку Xо, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х0 есть точка перегиба.
5.Асимптоты графика функции
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой. Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Говорят,
что прямая
х = а
является
вертикальной асимптотой
графика функции у
= f(х),
если
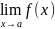 =∞,
или
=∞,
или
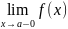 =∞,
или
=∞,
или =∞.
=∞.
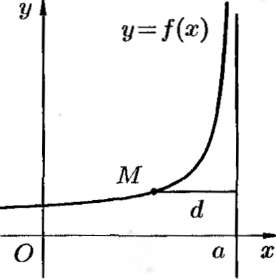
Горизонтальная
асимптота — прямая вида при условии
существования предела

Наклонная асимптота — прямая вида при условии существования пределов
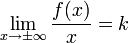

6.Общая схема исследования функции и построения графика
Исследование функции у=f(x) целесообразно вести в определенной последовательности.
Найти область определения функции.
Найти (если это можно) точки пересечения графика с осями координат.
Найти интервалы знакопостоянства функции (промежутки, на которых f(x) > 0 или f(x) < 0).
Выяснить, является ли функция четной, нечетной или общего вида.
Найти асимптоты графика функции.
Найти интервалы монотонности функции.
Найти экстремумы функции.
Найти интервалы выпуклости и точки перегиба графика функции.
На основании проведенного исследования построить график функции.
3.Глобальный экстремум на отрезке
Наибольшее
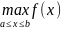 и наименьшее
и наименьшее
 значения непрерывной функции f
на отрезке [a;b]
называются глобальным max и min
соответственно или глобальным экстремумом.
Глобальный экстремум существует в силу
теоремы Вейерштрасса. Ясно, что точками
глобального экстремума могут быть точки
локального экстремума или концы отрезка.
Отсюда правило отыскания глобального
экстремума непрерывной функции f на
отрезке[a;b]:
значения непрерывной функции f
на отрезке [a;b]
называются глобальным max и min
соответственно или глобальным экстремумом.
Глобальный экстремум существует в силу
теоремы Вейерштрасса. Ясно, что точками
глобального экстремума могут быть точки
локального экстремума или концы отрезка.
Отсюда правило отыскания глобального
экстремума непрерывной функции f на
отрезке[a;b]:
1) Находим точки возможного экстремума на интервале (a,b)
2) Вычисляем значение функции f в этих точках и значения f(a), f(b)
Наибольшее из этих значений есть , а наименьшее -
2.Локальные экстремумы. Необходимое и достаточные условия существования экстремума
Точка
Хо называется
точкой максимума
функции
у
= f(x),
если существует такая -окрестность
точки X0,
что для всех x X0
из этой окрестности выполняется
неравенство f(x)
< f(Xо).Аналогично
определяется точка минимума функции:
Xо
—
точка минимума
функции, если
X0
из этой окрестности выполняется
неравенство f(x)
< f(Xо).Аналогично
определяется точка минимума функции:
Xо
—
точка минимума
функции, если
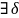 >
О
>
О
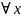 : 0 < |x
- X0|
<
: 0 < |x
- X0|
<
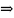 f(x)
>f(Xо).
Значение функции в точке максимума
(минимума) называется максимумом-
(минимумом)
функции. Максимум(минимум) функции
называется
экстремумом
функции.Понятие экстремума всегда
связано с определенной окрестностью
точки из области определения функции.
Поэтому функция может иметь экстремум
лишь
во внутренних точках
области определения.
f(x)
>f(Xо).
Значение функции в точке максимума
(минимума) называется максимумом-
(минимумом)
функции. Максимум(минимум) функции
называется
экстремумом
функции.Понятие экстремума всегда
связано с определенной окрестностью
точки из области определения функции.
Поэтому функция может иметь экстремум
лишь
во внутренних точках
области определения.
Необходимое условие экстремума. Если дифференцируемая функция у=f(x) имеет экстремум в точке Xо, то ее производная в этой точке равна нулю: f ' (Xо) = 0.
Достаточное условие экстремума. Если непрерывная функция у=f(x) дифференцируема в некоторой -окрестности критической точки Хо и при переходе через нее (слева направо) производная f'(x) меняет знак с плюса на минус, то Xо есть точка максимума; с минуса на плюс, то Xо — точка минимума.
