Глава 1. Нелокальные итерационные процессы для решения нелинейных уравнений локально сходящиеся с квадратичной скоростью

Глава посвящена решению уравнения

, – B-пространство (1.1)

с помощью нерегуляризованных, частично регуляризованных и регуляризованных итерационных процессов. Вначале будем полагать, что , а оператор непрерывно обратим. Здесь предполагается, что – производная Фреше оператора и в существует –решение уравнения (1.1), затем будем полагать, что непрерывно обратим оператор , где , – единичный оператор. В дальнейшем мы откажемся от требования гладкости оператора : будем полагать, что , первые разделённые разности оператора удовлетворяют условию Липшица в или вторые разделённые разности оператора равномерно ограничены в , а также оператор равномерно ограничен в . Здесь – оператор разделённой разности оператора , оператор – обратный оператору . Глава завершается рассмотрением полностью регуляризованных алгоритмов с негладкими операторами.

§ 1. Нелокальные нерегуляризованные итерационные процессы для решения уравнения (1.1), реализующие процедуру неполного прогноза-коррекции.

Для решения уравнения (1.1) рассматривается итерационный процесс в предположении, что оператор f в интересующей нас области D удовлетворяет следующим условиям:

, , , . (1.2)

Шаг 1. Решается линейное уравнение относительно :

n=0,1,2,… (1.3)

Шаг 2. Вносится поправка в вектор :

n=0,1,2,…, (1.4)

Шаг 3. Если < , где - малая величина (параметр останова), то конец просчётов, иначе переход на шаг 4.

Шаг 4. Определяется новая шаговая длина: если < то иначе

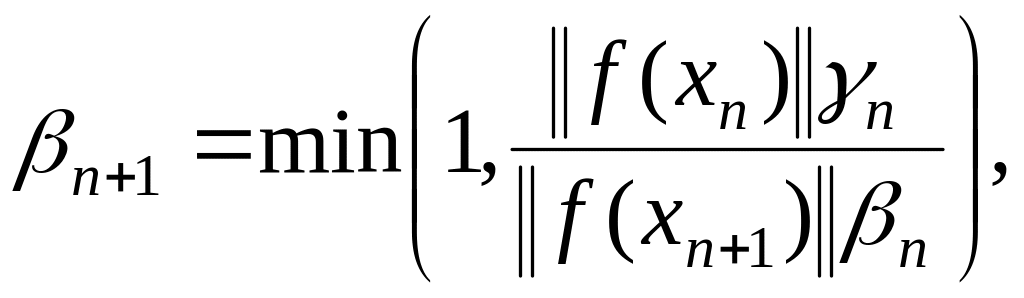
n=0,1,2,…, (1.5)

и осуществляется переход на шаг 1.

Теорема 1.1. Пусть оператор f удовлетворяет перечисленным выше условиям (1.2), в D существует - решение уравнения (1.1), начальное приближение и шаговая длина таковы, что выполняется условие <1. Тогда итерационный процесс (1.3)-(1.5) со сверхлинейной (локально квадратичной) скоростью сходится к

В нашем случае D – это шар с центром и радиусом

Доказательство. Пусть тогда для > n+2 справедливо соотношение, которое следует из (1.5)

. (1.6)

Из (1.6) имеем формулу, связывающую шаговые длины с нормами невязок:

. (1.7)

Из условий теоремы нетрудно получить оценку, связывающую нормы невязок на соседних шагах

, (1.8)

При n=0 из условий теоремы и (1.8) имеем:

< . (1.9)

Так, что из (1.5), (1.9) при n=0 следует, что > > , , < . Из (1.7), (1.8) следует , что и так как при n=1 имеем, что , то и < Аналогичные рассуждения при n=2 дают соотношения , , , . Тогда из (1.7), (1.8) методом математической индукции получим:

< > > . (1.10)

Таким образом, из (1.10) имеем, что последовательности итерационных параметров с чётными и нечётными индексами образуют монотонно возрастающие последовательности, ограниченные снизу числом , последовательности чётными и нечётными индексами образуют монотонно убывающие последовательности, ограниченные сверху числом откуда имеем, что последовательности с чётными и нечётными индексами образуют монотонно убывающие последовательности, ограниченные сверху числом . Из (1.8) и вышесказанного имеем оценку:

(1.11)

из которой следует, что

при (1.12)

Таким образом, из (1.12) имеем, что последовательность элементов по функционалу и все элементы последовательности принадлежат шару

Рассмотрим вопрос о том, существует ли такой номер , что для . Из (1.5) имеем, что при таком :

.

В числителе правой части последнего неравенства константа, а знаменатель стремится к нулю при , так что найдется такой номер , при котором и, следовательно, все для .

Кроме того, из (1.11) следует, что существует такой номер , начиная с которого станет выполняться неравенство так что, начиная с начинает выполняться достаточное условие сходимости метода Ньютона. С этого момента процесс (1.3)-(1.5) переходит в метод Ньютона с характерной для последнего квадратичной скоростью сходимости. Теорема доказана.

Ослабим требования на оператор .

Теорема 1.2 Пусть в шаре существует – решение уравнения (1.1), оператор , удовлетворяет условию и . Если начальное приближение и шаговая длина таковы, что , , тогда итерационный процесс (1.3) – (1.5) сходится к и оценка погрешности -го приближения имеет вид:

.

Доказательство. В силу условий теоремы справедливо соотношение

,

из которого следует оценка

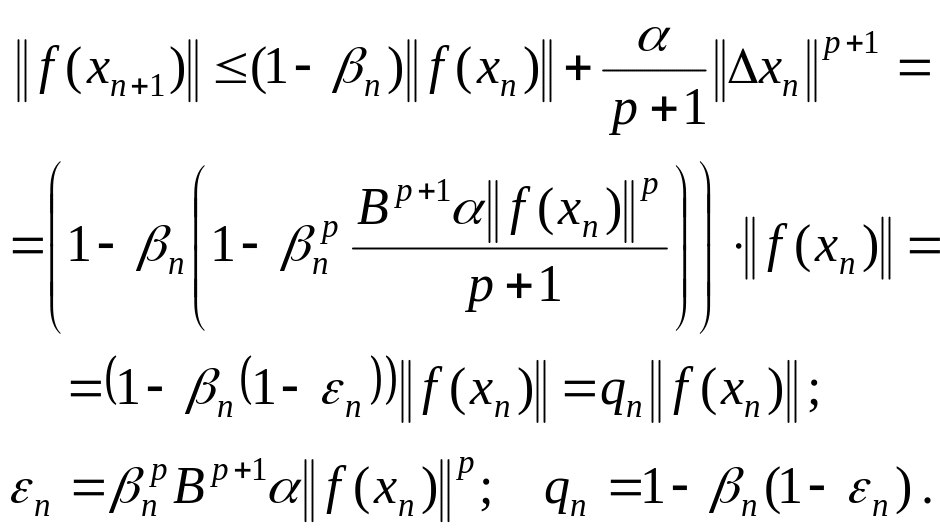(1.13)

При из условия теоремы имеем

, , , ,

, .

.

Из (1.7) в силу справедливости соотношения, связывающего шаговые длины и нормы невязок при , имеем оценки

,

, .

Индуктивные рассуждения позволяют получить оценки

; (1.14)

. (1.15)

Из (1.14) следует слабая сходимость последовательности элементов , генерируемая процессом (1.3)–(1.5), к , а из (1.15) следует фундаментальность последовательности и в силу полноты пространства имеет место и сильная сходимость последовательности элементов к , а также то, что все .

Оценка погрешности -го приближения получается при переходе к пределу в (1.15) при . Теорема доказана.

Теорема 1.3. Пусть в шаре 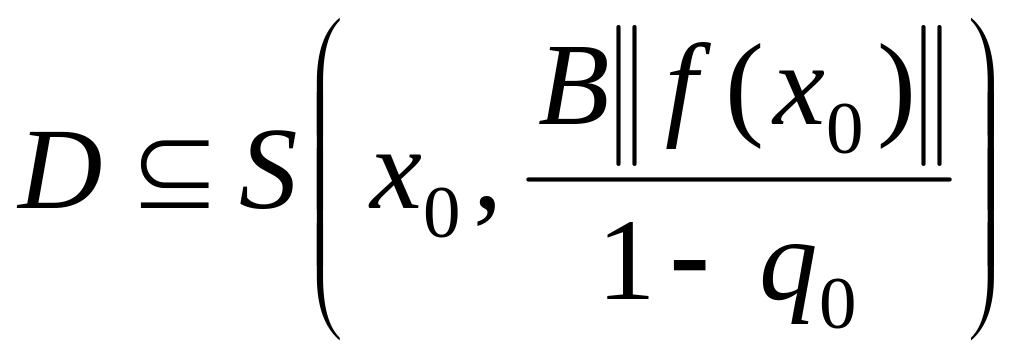, существует – решение уравнения (1.1) и производная оператора в смысле Фреше удовлетворяет условию Липшица с некоторой константой . Если , начальное приближение и шаговая длина таковы, что , то итерационный процесс (1.3)–(1.5) со сверхлинейной скоростью сходится к .

Здесь .

Доказательство. В силу условий теоремы справедливо соотношение:

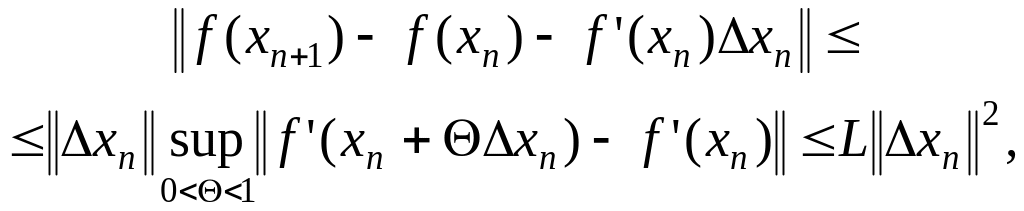
из которого следует оценка

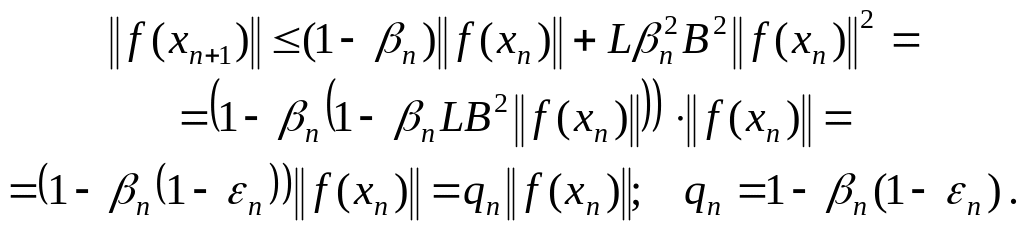(1.16)

Доказательство теоремы опирается на (1.16) и дословно повторяет доказательство теоремы 1.2.

Теорема 1.4. Пусть в сфере выполнены условия теоремы 1.3 кроме факта a priori существования решения . Пусть существует целое положительное число такое, что

, .

, , .

Тогда уравнение (1.1) имеет решение , к которому сходится итерационный процесс (1.3)–(1.5), начиная с . Скорость сходимости к определяется неравенством

. (1.17)

Доказательство. Так как выполняются все условия теоремы (1.1) за исключением a priori факта существования в , то существует номер такой, что и

Следовательно, , а это есть не что иное, как достаточное условие сходимости метода Ньютона. И, таким образом, в сфере существует решение . Оценка (1.17) получается стандартным образом. Теорема доказана.

Теорема, аналогичная теореме 1.4 может быть доказана и в случае, если имеют место соотношения

. (1.18)

Здесь вторая производная в смысле Гато.

Теорема 1.5. Пусть в существует – решение уравнения 1.1 и в выполняются условия (1.18). Если и таковы, что , тогда итерационный процесс (1.3)–(1.5) со сверхлинейной скоростью сходится к .

Доказательство. В силу условий теоремы справедливо соотношение:

, из которого следует оценка

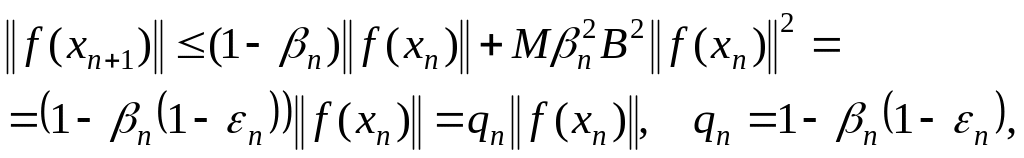(1.19)

Из (1.7) и условий теоремы при имеем, что , . Тогда .

Индуктивные рассуждения позволяют получить оценку

, , (1.20)

из которой следует, что последовательность , генерируемая процессом (1.3)-(1.5), по функционалу стремится к . Из оценки (1.20)

(1.21)

следует фундаментальность последовательности , откуда в силу полноты пространства следует сильная сходимость последовательности к – предельному элементу последовательности, который является решением уравнения (1.1).

Из (1.20) следует, что в процессе счета найдется такой номер , что для всех и при этом , тогда из (1.19) имеем, что

и если , то ,

откуда следует локальная квадратичная сходимость итерационного процесса (1.3)–(1.5) к . Теорема доказана.

Для решения уравнения (1.1) эффективным оказывается итерационный процесс.

Шаг 1 Решается линейное уравнение относительно

(1.22)

Шаг 2 Вносится поправка в вектор

(1.23)

Шаг 3 Если (параметр останова), то конец просчетов, иначе

Шаг 4 Определяется новая шаговая длина: если , то принимает значение 1, иначе

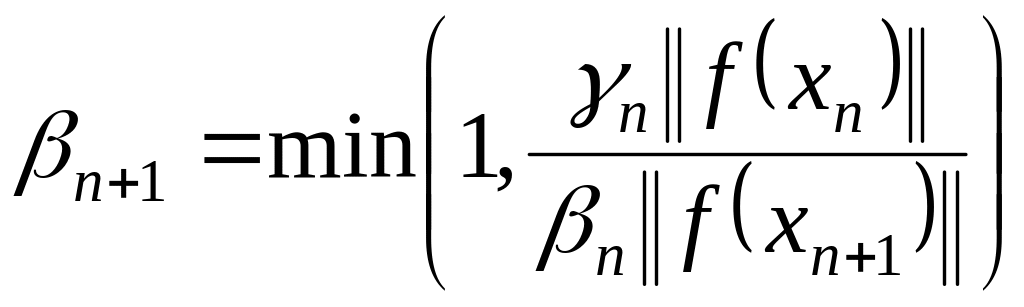, (1.24)

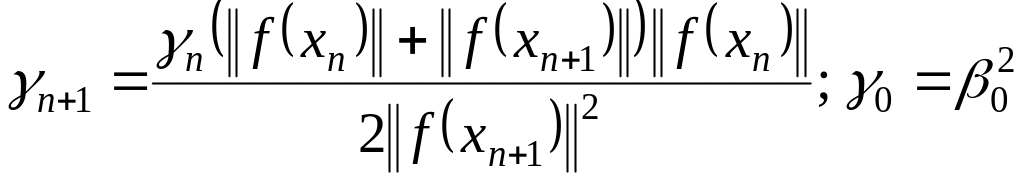
и осуществляется переход на шаг 1.

Теорема 1.6. Пусть оператор удовлетворяет в условиям теоремы 1.1. Тогда итерационный процесс (1.22) – (1.24) со сверхлинейной (локально с квадратичной) скоростью сходится к , .

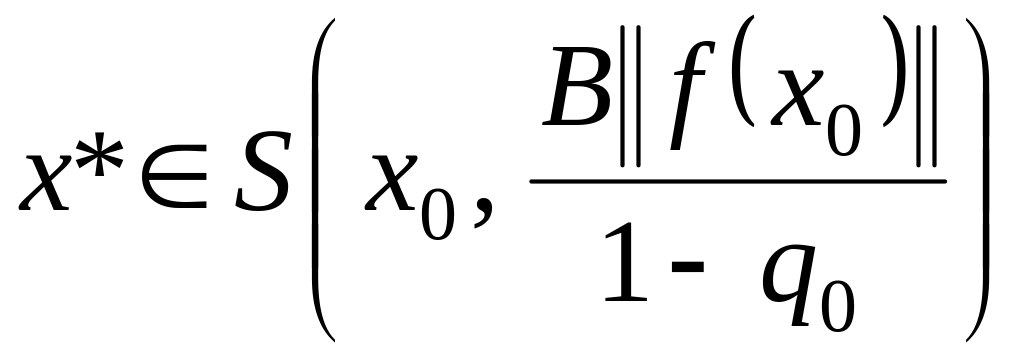Доказательство. Пусть , тогда для имеет место соотношение, которое следует из (1.24)

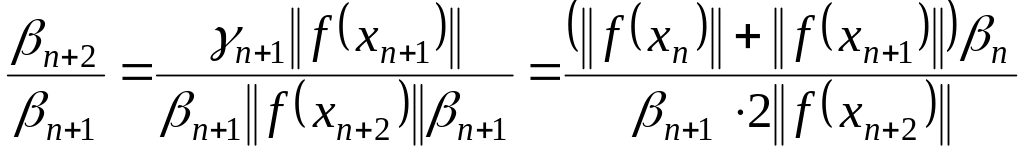. (1.25)

Из (1.25) имеем соотношение, связывающее шаговые длины и нормы невязок

. (1.26)

Из условий теоремы имеем оценку, связывающую нормы невязок на соседних шагах

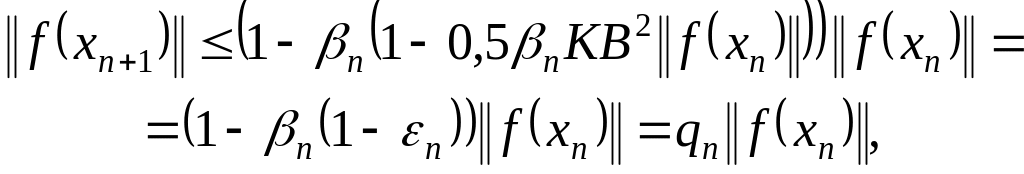(1.27)

, .

Если , то из (1.27) следует, что , а из (1.24) имеем, что , тогда . Из (1.24), (1.26) следует справедливость неравенств , , . Индуктивно нетрудно показать, что последовательности с четными и нечетными индексами монотонно убывают и ограничены сверху числом (при ), последовательность норм невязок монотонно убывает и ограничена сверху числом , последовательности с четными и нечетными номерами образуют монотонно возрастающие последовательности, ограниченные снизу числом , так что последовательности с четными и нечетными индексами образуют монотонно убывающие и ограниченные сверху числом последовательности.

Из (1.27) и вышесказанного имеем оценку

, (1.28)

из которой следует, что при . Таким образом, последовательность элементов по функционалу и все элементы последовательности принадлежат шару 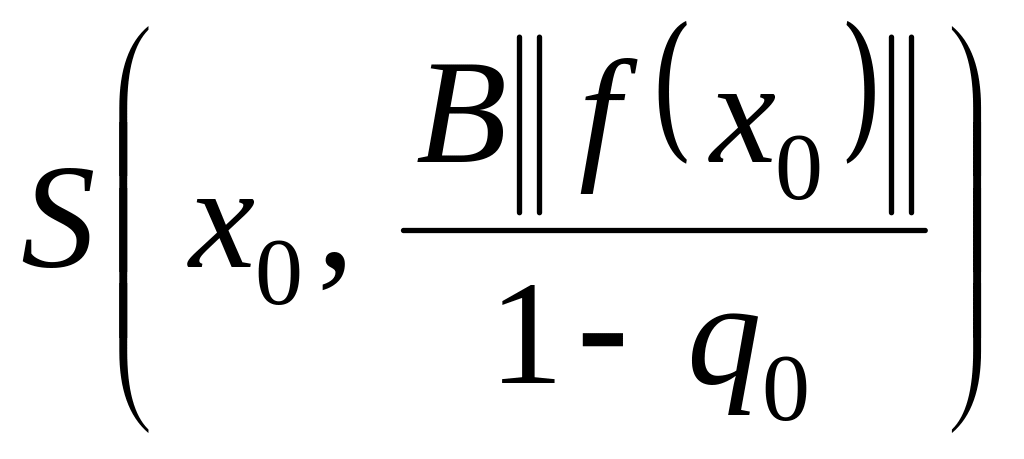. Из (1.24) и того факта, что последовательность монотонно возрастает, следует, что если , то справедлива цепочка неравенств

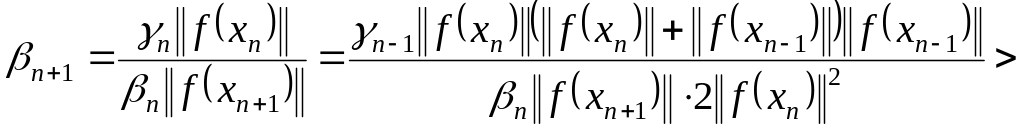
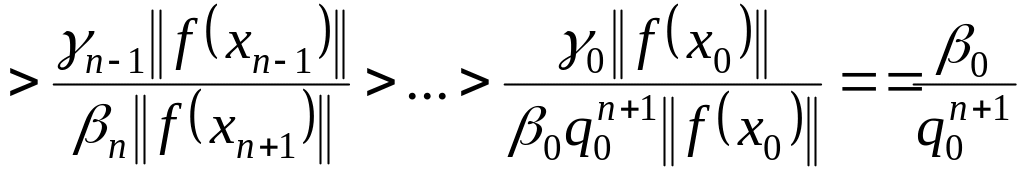. (1.29)

Из (1.29) имеем, что существует такой номер , что для всех шаговая длина .

В связи с вышесказанным и из (1.28) имеем, что существует такой номер , начиная с которого выполнятся достаточное условие сходимости метода Ньютона , откуда следует локальная квадратичная сходимость процесса (1.22) – (1.24). Теорема доказана.

Замечание 1. Эффективность процессов (1.3)–(1.5) и (1.22)–(1.24) может быть несколько усилена за счет введения в множителя .

Теорема 1.7. Пусть в шаре выполняются условия теоремы 1.1 за исключением требования факта существования a priori . Пусть существует такое , что

, ,

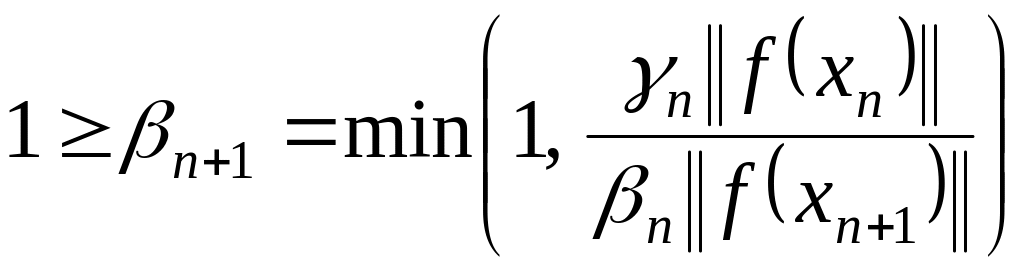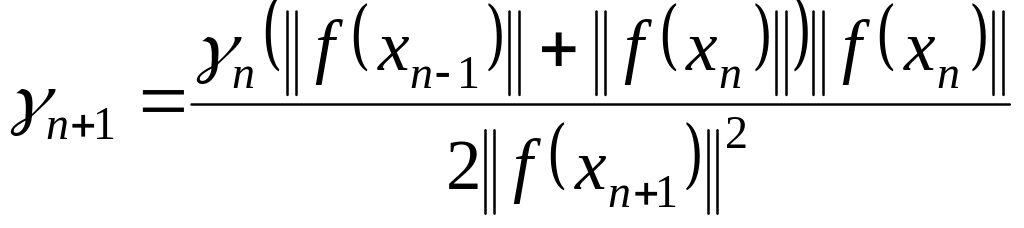; , (1.30)

, ,

Тогда уравнение (1.1) имеет решение , к которому сходится итерационный процесс (1.22) – (1.24), начиная с и имеет место оценка погрешности -ого приближения

. (1.31)

Доказательство. Доказательство опирается на соотношения (1.28) – (1.30), из которых следует, что существует номер такой, что . Поскольку это есть достаточное условие сходимости метода Ньютона, то в шаре S существует решение . Оценка (1.31) получена стандартным образом для n>l. Теорема доказана.

Теоремы, аналогичные теоремам 1.2, 1.3, 1.5 могут быть сформулированы и доказаны применительно к итерационному процессу (1.22)–(1.24). Предоставляем это выполнить в качестве упражнения.

К числу достаточно эффективных одношаговых процессов может быть отнесен процесс вида:

Шаг 1. Решаем линейное уравнение

. (1.32)

Шаг 2. Находим очередное приближение

(1.33)

Шаг 3. Если (параметр останова), то конец просчетов, иначе

Шаг 4. Определяется новая шаговая длина: если , то принимает значение 1, иначе

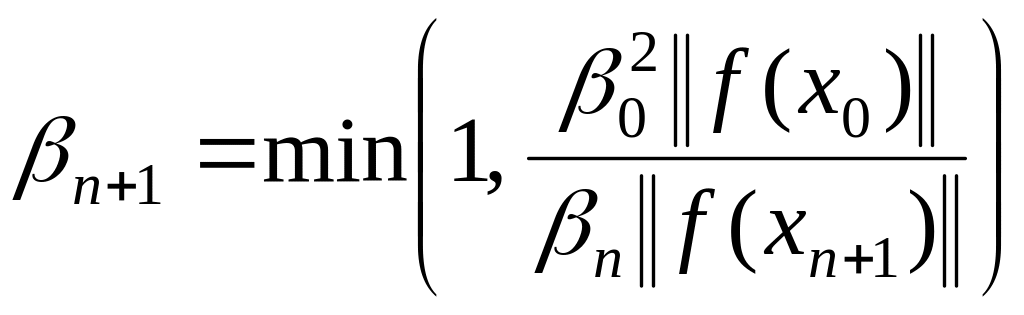(1.34)

и осуществляется переход на шаг 1.

Теорема 1.8. Пусть в шаре 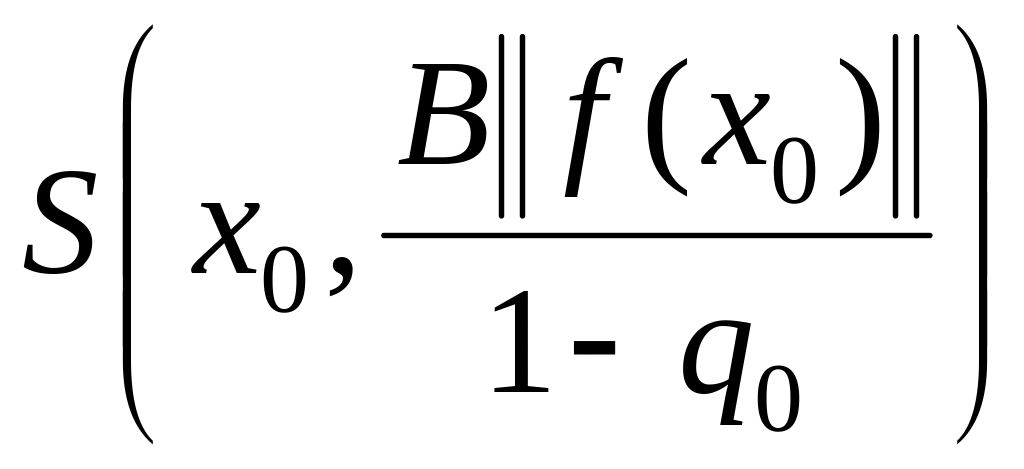выполняются условия теоремы 1.1. Тогда итерационный процесс (1.32) – (1.34) при со сверхлинейной (локально с квадратичной) скоростью сходится к .

Доказательство. Найдем соотношение, связывающее шаговые длины и нормы невязок. Полагая, что , в силу (1.34) имеем , откуда следует нужное для доказательства теоремы соотношение

. (1.35)

Рассуждениями, вполне аналогичными тем, которые были проведены в процессе доказательства теоремы 1.1, доказывается, что последовательность итерационных параметров , последовательность норм невязок , последовательность , монотонно убывает к нулю и справедлива оценка

. (1.36)

Покажем, что существует такой номер i=n+1, начиная с которого . Если , то из (1.34) имеем

. (1.37)

Из (1.37) в силу (1.36) следует, что так как числитель в правой части (1.37) является константой, а знаменатель может быть сделан достаточно малым, то существует такой номер i>n+1, что и все . Из (1.36) и вышесказанного следует, что существует номер такой, что

. (1.38)

Соотношение (1.38) есть достаточное условие сходимости метода Ньютона и, начиная с этого номера, процесс (1.32) – (1.34) непременно переходит в метод Ньютона с характерной для последнего локальной квадратичной скоростью. Теорема доказана.

Теоремы, аналогичные теоремам 1.2–1.5 могут быть сформулированы и доказаны применительно к алгоритму (1.32) – (1.34).

Достаточно эффективным с вычислительной точки зрения является процесс вида:

Шаг 1. Решается линейная система для определения поправки

(1.39)

Шаг 2. Вносится поправка в вектор :

(1.40)

Шаг 3. Если (параметр останова), то конец просчетов, иначе Шаг 4. Определяется новая шаговая длина: если , то , иначе

; (1.41)

и осуществляется переход на шаг 1.

Относительно процесса (1.39) – (1.41) может быть сформулирована и доказана

Теорема 1.9. Пусть выполняется условие теоремы 1.1 в интересующем нас шаре , . Тогда итерационный процесс (1.39)–(1.41) при со сверхлинейной (локально с квадратичной) скоростью сходится к .

Доказательство. Доказательство опирается на соотношение, связывающее шаговые длины с нормами невязок, которое следует из (1.41). Если то из (1.41) имеем:

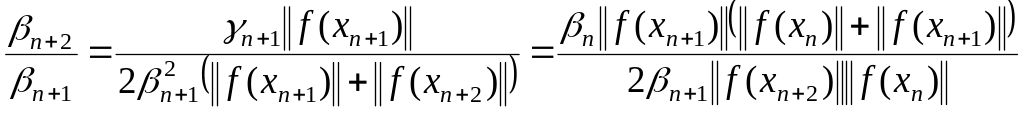. (1.42)

Из (1.42) следует, что

. (1.43)

Рассуждения, аналогичные тем, что приведены при доказательстве теоремы 1.1, дают оценку

, (1.44)

где , .

Из (1.43) имеем, что последовательность итерационных параметров , последовательность образует монотонно убывающую последовательность, ограниченную сверху числом , последовательности с четными и нечетными номерами монотонно убывает при , последовательность норм .

Нетрудно показать, что в условиях теоремы существует такой номер , что для . Далее, из (1.44) имеем, что существует такой номер , что . Таким образом, взяв , имеем, что, начиная с номера , начинает выполняться достаточное условие сходимости метода Ньютона и утверждения теоремы 1.9 справедливы.

Оценка погрешности -ого приближения получается, как и выше. Теорема доказана.

Теоремы, аналогичные теоремам 1.2 – 1.5, могут быть сформулированы и доказаны применительно к процессу (1.39)-(1.41).

Среди одношаговых методов неполного прогноза достаточно эффективным оказывается следующий итерационный процесс

Шаг 1 Решается линейная система

для определения поправки

… (1.45)

Шаг 2 Вносится поправка в , определяется очередное приближение

. (1.46)

Шаг 3 Проверяется условие окончания итерационного процесса: если , – параметр останова, то конец просчетов, иначе переход на

Шаг 4 Определяется новая шаговая длина: если , то , иначе производится пересчет по формуле

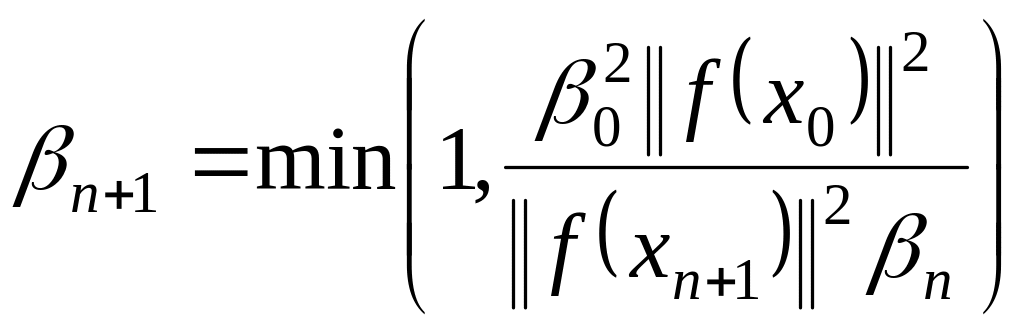, (1.47)

и осуществляется переход на шаг 1.

Относительно процесса (1.47) – (1.49) справедлива

Теорема 1.10. Пусть в шаре , выполняются условия теоремы 1.1. Тогда итерационный процесс (1.45)–(1.47) при со сверхлинейной (локально с квадратичной) скоростью сходится к . .

Оценка погрешности -ого приближения имеет вид

. (1.48)

Доказательство. Найдем соотношение, связывающее шаговые длины с нормами невязок, для чего возьмем отношение к , полагая, что . С учетом (1.47) имеем

.

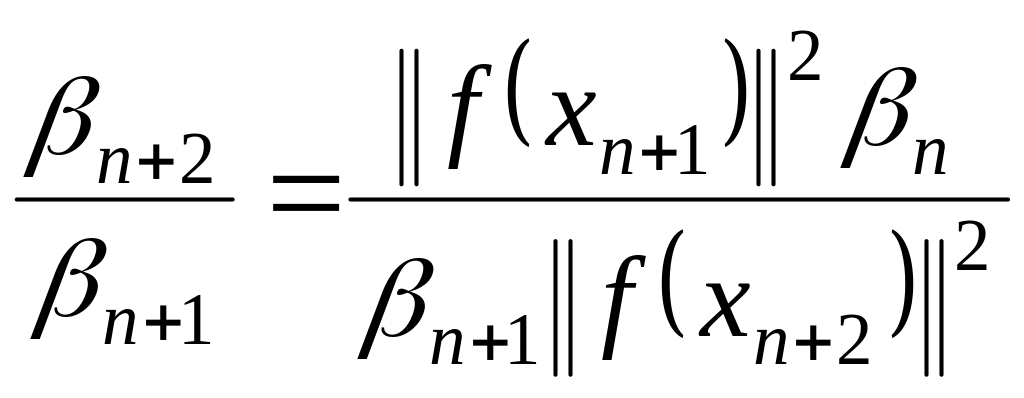Из последнего соотношения следует равенство

. (1.49)

Рассуждения, вполне аналогичные тем, что приведены в теореме 1.1, дают возможность утверждать, что последовательности шаговых длин (итерационных параметров) с четными и нечетными индексами монотонно возрастают и ограничены снизу числом , последова-тельности с четными и нечетными индексами монотонно убывают и ограничены сверху числом , последовательность монотонно убывает и ограничена сверху числом , последовательность норм невязок монотонно убывает к нулю и имеет место оценка

. (1.50)

С учетом (1.47), (1.50) при имеет место неравенство

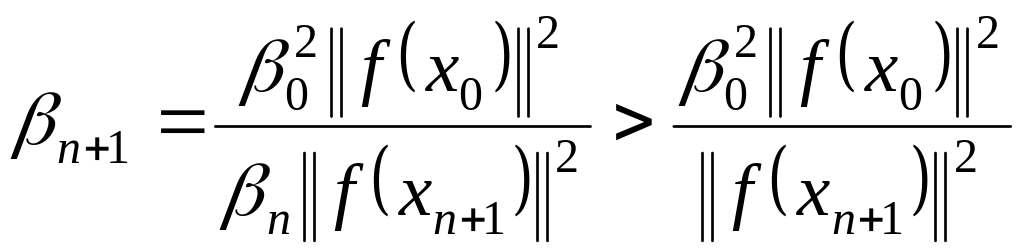. (1.51)

Так как в правой части неравенства (1.51) в числителе стоит константа, а знаменатель, в силу (1.50), может быть сделан в процессе счета сколь угодно малым, то существует такой номер , что для становится равным 1, в силу (1.50) существует такой номер , что . Таким образом, при начинает выполняться достаточное условие сходимости метода Ньютона. Оценка погрешности -ого приближения получается стандартным образом. Теорема доказана.

Теоремы, аналогичные теоремам 1.2 – 1.5, могут быть сформулированы и доказаны применительно к процессу (1.45)–(1.47).

Если область определить другим способом, чем это мы делали выше, то может быть описан еще ряд эффективных процессов.

Пусть оператор удовлетворяет в области условиям: , линейный оператор в обратим и имеют место оценки

Здесь – производная Фреше оператора .

Определим область так: . Для решения уравнения (1.1) применим процесс вида

Шаг 1. Решается линейное уравнение

(1.52)

Шаг 2. Находим очередное приближение

(1.53)

Шаг 3. Если < , <<1 (параметр останова), то конец просчётов, иначе

Шаг 4. Определяется новая шаговая длина: если < , то принимает значение 1, иначе

(1.54)

, (1.55)

и осуществляется переход на шаг 1.

Теорема 1.11. Пусть в области D существует – решение уравнения (1.1), оператор удовлетворяет перечисленным выше условиям. Пусть сверх того, выполняются условия:

а)

б) .

Тогда итерационный процесс (1.52)–(1.55) со сверхлинейной скоростью сходится к и .

Доказательство. Подставляя (1.54) в (1.55) и применяя индукцию, имеем соотношение

, (1.56)

из которого следует ограниченность последовательности чисел , которая определяется формулами (1.54), (1.55), а также их монотонное убывание с ростом номера . Из (1.54) нетрудно получить соотношение

(1.57)

которое при замене на имеет вид

. (1.58)

Деля соотношение, определяемое (1.57) на соотношение (1.58), имеем оценку, связывающую шаговую длину с нормой невязки

(1.59)

В силу условий теоремы справедлива оценка

, (1.60)

Найдём условия, при которых все . Пусть , тогда из (1.60) следует, что

и если , то из последнего неравенства следует, что .

Пусть n=1. Тогда из (1.60) имеем, что

(1.61)

или с учётом (1.54) при оценка (1.61) примет вид

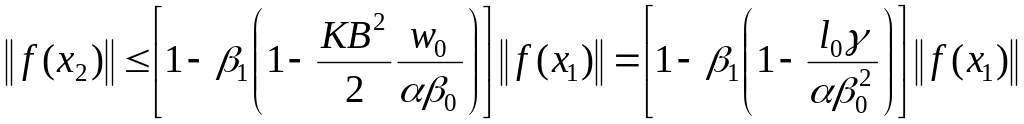(1.62)

Если , то .

Пусть , тогда в силу (1.59), (1.60) имеем

Индуктивные рассуждения позволяют получить оценку

, (1.63)

из которой с очевидностью следует сходимость по функционалу к последовательности элементов , образованной итерационным процессом (1.52)-(1.55), а также сильная (по норме) сходимость элементов последовательности к .

Действительно, из (1.52) – (1.55) и условий теоремы следуют оценки

, .

,

из которых следует фундаментальность последовательности . В силу полноты пространства X имеем, что .

Переходя к пределу в последнем неравенстве при и имея в виду по выше доказанному, что – решение уравнения (1.1), получим, что при , откуда следует утверждение о сильной сходимости к .

Далее, покажем, что (;/0 при . Положив противное, имеем, из (1.54) что стремиться к пределу со сверхлинейной скоростью, а из (1.55) следует, что стремится к пределу со скоростью не быстрее линейной. Противоречие будет снято, если отказаться от предположения о том, что при .

В связи с тем, что (;/0 при , ряд расходится, следовательно, расходится к нулю бесконечное произведение . Таким образом, как следует из (1.56), и при этом для “хороших” задач порядки убывания и , как правило, совпадают. Стандартными рассуждениями нетрудно показать, что все последовательные приближения и . Теорема доказана.

Замечание 2. Как следует из (1.55), аппроксимирует , а из (1.63) видно, что существует такой номер , что для всех начинает выполнятся достаточное условие сходимости метода Ньютона. Если , тогда попадает в область притяжения метода Ньютона и мы можем рассчитывать на локальную квадратичную сходимость процесса (1.52)-(1.55).

Теорема 1.11 справедлива в предположении существования в – решения уравнения (1.1). Сформулируем и докажем теорему, в которой будут использованы доказательные вычисления.

Теорема 1.12. Пусть в области оператор , и, сверх того, выполняются условия:

а) ,

b) ,

c) начиная с некоторого номера ,

тогда итерационный процесс (1.52)-(1.55) со сверхлинейной (локально с квадратичной) скоростью сходится к .

Доказательство. Вполне аналогично тому, как это было сделано при доказательстве теоремы 1.11, могут быть получены оценки вида (1.63)

и если, начиная с k-го шага, , а, начиная с -го шага, выполняется достаточное условие сходимости метода Ньютона, то, взяв будем иметь, что точка попадает в область притяжения метода Ньютона и налицо локальная квадратичная скорость сходимости и существование решения . Теорема доказана.

Теоремы, аналогичные теоремам 1.2–1.5 могут быть сформулированы и доказаны и относительно процесса (1.52)–(1.55)

Замечание 3. Эффективная проверка условий (1.2) часто затруднительна, оценки для и получаются завышенными, радиус интересующей нас сферы содержит глобальную константу . Все вышесказанное требует осуществить поиск других путей определения радиуса области D.

Замечание 4. Обратимость оператора в области является также достаточно обременительным условием.

В связи с вышесказанным, следуя идее работы [60], найдем условия, при которых при переходе от точки , в которой существует, к точке будет существовать ограниченный обратный оператор . Если , имеем оценку

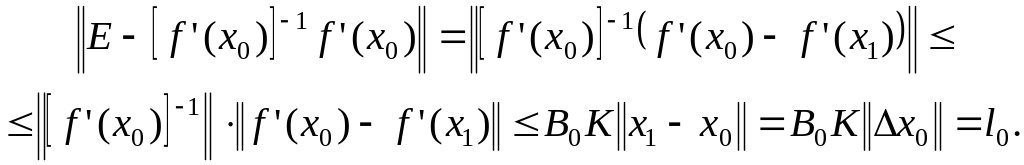
Здесь , – единичный оператор.

Если , то в силу теоремы Банаха существует оператор обратный оператору и справедлива оценка .

Если для получения элемента использовать метод Ньютона, имеем оценку

. (1.64)

Определим так, чтобы при переходе от точки к точке выполнялось неравенство . Имеем

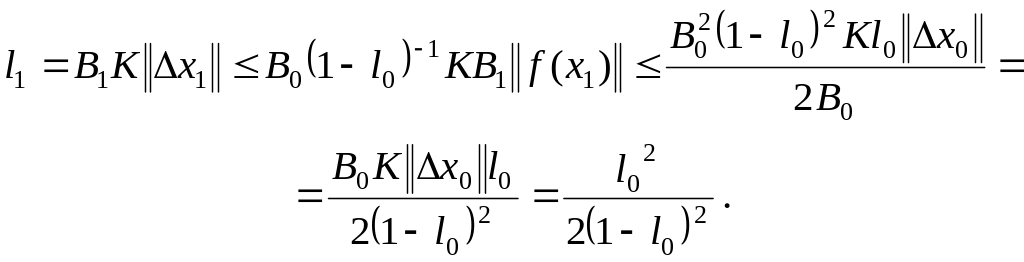
Неравенство справедливо при . Нетрудно найти радиус области существования решения уравнения (1.1) в сфере . Учитывая (1.64), имеем оценку для сходящегося процесса Ньютона

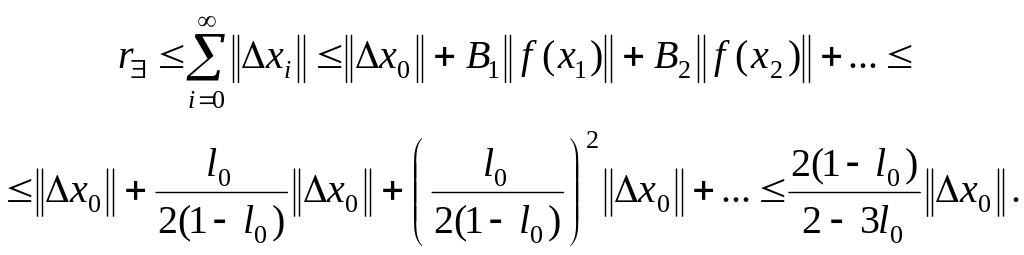(1.65)

Наряду с оценкой (1.65) может быть получена оценка (1.66).

(1.66)

Найдем условия, при выполнении которых в области не более одного решения. Положим, что существуют два решения и . Тогда справедлива оценка:

(1.67)

Если в (1.67) потребовать, чтобы или

, (1.68) то в сфере будет не более одного решения.

В условиях сходящегося процесса Ньютона рассмотрим неравенство

, (1.69) которое равносильно утверждению . Из (1.69) следует оценка :

(1.70)

Если в качестве взять правую часть соотношения (1.66) и потребовать выполнения условия

(1.71) то неравенство (1.71) также равносильно утверждению того, что .

Из (1.71) имеем соотношение, связывающее нормы поправок на соседних шагах:

. (1.72)

Так как , то . Тогда из выполнения соотношения (1.73)

. (1.73) будет следовать соотношение (1.72), которое является следствием утверждения того, что .

Пусть выполняется (1.73). Тогда соотношение (1.73) можно переписать в следующем виде:

. (1.74)

Левая часть неравенства (1.74) мажорирует правую часть соотношения (1.66), а правая часть (1.74) минорирует правую часть (1.69). Следовательно, из выполнения (1.73) следует выполнение (1.72), которое есть условие того, что . Таким образом, нами доказана теорема

Теорема 1.13. Пусть оператор , . На некотором шаге сходящегося процесса Ньютона выполняется соотношение

. Тогда в сфере решение уравнения (1.1) существует и единственно.

Замечание 5. Доказанная выше теорема 1.13 относится к классу так называемых «доказательных» вычислений, поскольку вся необходимая информация получается в результате работы вычислительного алгоритма.

Весьма эффективным с вычислительной точки зрения являются многошаговые методы неполного прогноза, одним из представителей которого является следующий алгоритм

Шаг 1. Решается линейная система для определения поправки

(1.75)

Шаг 2. Находим очередное приближение

. (1.76)

Шаг 3. Если (параметр останова), то конец просчетов, иначе

Шаг 4. Определяется новая шаговая длина, если , то , иначе

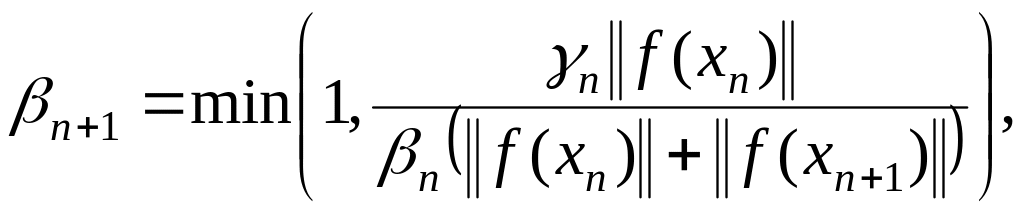(1.77)

и переход на шаг 1

Теорема 1.14. Пусть в сфере выполняются условия теоремы 1.1. Тогда итерационный процесс (1.75) - (1.77) при со сверхлинейной (локально с квадратичной) скоростью сходится к и имеет место оценка погрешности ого приближения

.

Доказательство. Пусть , тогда имеем в силу (1.77)

_(1.78)

Из (1.78) имеем соотношение, связывающее шаговые длины и нормы невязок

(1.79)

Из (1.77) и условий теоремы следует, что , , . Из (1.79) имеем, что с четными и нечетными индексами образуют монотонно убывающие последовательности, ограниченные сверху числом , шаговые длины с четными и нечетными индексами образуют монотонно возрастающие последовательности, ограниченные снизу числом , образуют монотонно убывающую последовательность, ограниченную сверху числом , и справедлива оценка

при (1.80)

Из (1.80) следует сходимость последовательности элементов , генерируемых алгоритмом (1.75)-(1.77) к .

Далее, из (1.77) имеем оценку при

_(1.81)

Из (1.80), (1.81) следует что, начиная с некоторого номера , все шаговые длины становятся равными единице.

Если при некотором номере начинает выполняться условие (достаточное условие сходимости метода Ньютона), то имеет место локальная квадратичная скорость сходимости процесса. Оценка n–ого приближения может быть получена стандартным способом. Теорема доказана.

Теоремы аналогичные теоремам 1.2–1.5, могут быть сформулированы и доказаны относительно процесса (1.75) – (1.77).

Вычислительная практика решения существенно нелинейных систем показывает эффективность следующего алгоритма:

Шаг 1 Решается линейная система для определения поправки

(1.82)

Шаг 2 Вносится поправка в вектор

. (1.83)

Шаг 3 Если ( –параметр останова), то конец просчетов, иначе

Шаг 4 Если , то , иначе

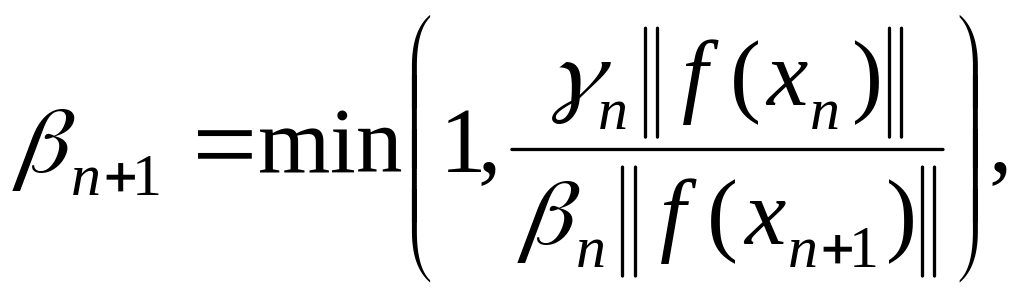(1.84)

.

и переход на шаг 1

Относительно алгоритма (1.82) – (1.84) справедлива

Теорема 1.15. Пусть в сфере выполняются условия теоремы 1.1. Тогда итерационный процесс (1.82) – (1.84) при со сверхлинейной (локально с квадратичной) скоростью сходится к . , .

Доказательство. Найдем соотношение, связывающее шаговые длины и нормы невязок, полагая, что шаговые длины меньше единицы. Из (1.84) имеем

_(1.85)

= .

Из (1.85) получаем необходимое соотношение

(1.86)

Рассуждениями, вполне аналогичными тем, которые приведены в доказательстве теоремы 1.14 с учетом (1.86), приходим к выводу о том, что последовательность итерационных параметров с четными и нечетными индексами монотонно возрастают и ограничены снизу числом , последовательности с четными и нечетными индексами монотонно убывают, все монотонно убывают и имеет место оценка

(1.87)

Далее из (1.84) имеем при , что

(1.88)

Из (1.87), (1.88) следует, что существует такой номер , что и . Таким образом, выполняется достаточное условие сходимости метода Ньютона и итерационный процесс, начиная с этого номера, переходит в метод Ньютона с характерной для последнего квадратичной скоростью сходимости. Теорема доказана.

Относительно процесса (1.82)-(1.84) могут быть сформулированы и доказаны теоремы, аналогичные теоремам 1.2 – 1.5.

Далее рассмотрим алгоритм

Шаг 1. Решается линейная система для определения поправки

(1.89)

Шаг 2. Находим очередное приближение

. (1.90)

Шаг 3. Если (параметр останова), то конец просчетов, иначе

Шаг 4. Определяется новая шаговая длина, если , то , иначе

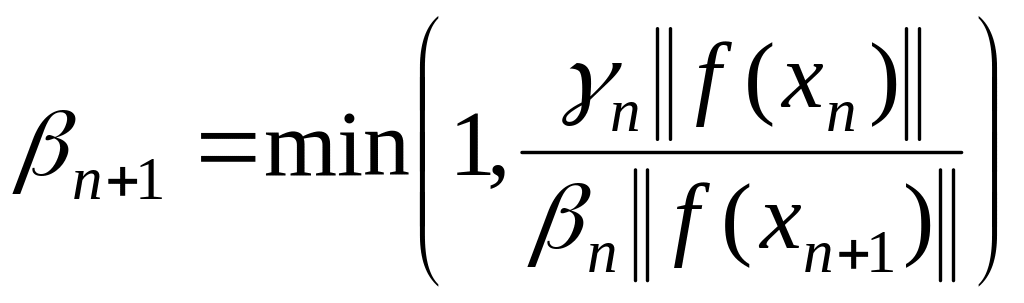; (1.91)

; .

Относительно процесса (1.89) – (1.91) справедлива

Теорема 1.16. Пусть в шаре выполняются условия теоремы 1.1. Тогда итерационный процесс (1.89) – (1.91) при со сверхлинейной (локально с квадратичной) скоростью сходится к . , .

Доказательство. Доказательство опирается на соотношение связывающее шаговые длины и нормы невязок. Пусть , тогда из (1.91) имеем

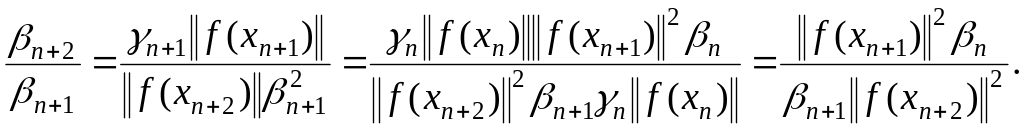(1.92)

Из (1.92) следует, что

(1.93)

Рассуждения, вполне аналогичные вышеприведенным, позволяют утверждать, что последовательности итерационных параметров с четными и нечетными индексами монотонно возрастают, последовательности , где с четными и нечетными номерами монотонно убывают и ограниченны сверху числом . Справедлива оценка

. (1.94)

Из (1.91) имеем, что

.

Из последнего соотношения и (1.94) следует, что при некотором параметр становится равным единице и существует такой номер , что начинает выполняться достаточное условие . Взяв , имеем, что и . Таким образом, начиная с i–ой начинает выполняться условие сходимости метода Ньютона и процесс (1.89)–(1.91) становится сверхлинейным (локально квадратичным). Теорема доказана.

Теоремы аналогичные теоремам 1.2–1.5 могут быть сформулированы и доказаны относительно процесса (1.89) – (1.91).

Следующим эффективным многошаговым итерационным процессом является алгоритм

Шаг 1. Решается линейная система для определения поправки

(1.95)

Шаг 2. Находим очередное приближение

. (1.96)

Шаг 3. Если (параметр останова), то конец просчетов, иначе

Шаг 4. Определяется новая шаговая длина, если , то , иначе

; ; . (1.97)

Относительно процесса (1.95) – (1.97) справедлива

Теорема 1.17. Пусть в шаре налагаются условия теоремы 1.1. Тогда итерационный процесс (1.95) – (1.97) при со сверхлинейной (локально с квадратичной) сходится к . .

Доказательство. При доказательстве теоремы обратим внимание на два факта: наличие связи между шаговыми длинами и нормами невязок и то, что существует номер такой, начиная с которого все .

Взяв отношение при из (1.97) имеем

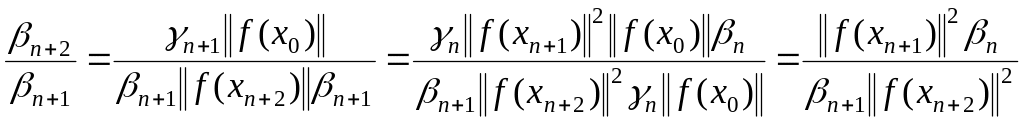(1.98)

Из (1.98) следует соотношение

. (1.99)

Из (1.99) и условий теоремы следует монотонное убывание норм невязок и оценка аналогичная (1.94).Далее,

(1.100)

Из (1.100) следует, что существует такой номер , что , а из (1.94) следует, что при некотором номере m , так что если , то и . Итак, начиная с номера i, выполняется достаточное условие сходимости метода Ньютона. Теорема доказана.

Теоремы аналогичные теоремам 1.2–1.5 могут быть сформулированы и доказаны относительно процесса (1.95)–(1.97)

Среди многошаговых нелокальных сверхлинейных итерационных процессов, реализующих процедуру неполного прогноза, интересен следующий процесс.

Шаг 1. Решается линейная система для определения поправки

(1.101)

Шаг 2. Находим очередное приближение

. (1.102)

Шаг 3. Если (параметр останова), то конец просчетов, иначе

Шаг 4. Определяется новая шаговая длина, если , то

(1.103)

,

Имеет место

Теорема 1.18. Пусть в сфере выполняются условие теоремы 1.1. Тогда итерационный процесс (1.101) – (1.103) при со сверхлинейной (локально с квадратичной) скоростью сходится к . .

Доказательство. Найдем соотношение, связывающее шаговые длины с нормами невязок. Если , то имеем в силу (1.103)

(1.104)

=

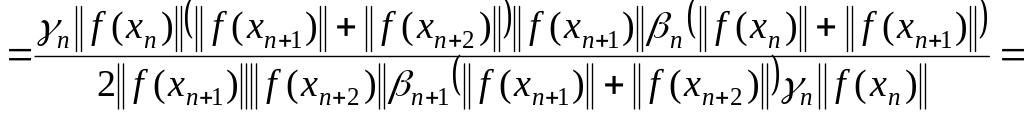
Из (1.104) имеем

. (1.105)

Вполне аналогично тому, как это мы делали выше с учетом (1.105), доказываем монотонное убывание норм невязок, стремление к нулю последовательности норм невязок, монотонное возрастание последовательностей с четными и нечетными номерами.

Если , то из (1.103) может быть получена оценка

(1.106)

Из (1.106) следует, что существует такой номер , что становится равным единице и такой номер m, что становится меньше единицы, так что взяв i=max(m,k), можно утверждать что с этого номера итерации начинает выполнятся достаточное условие сходимости метода Ньютона и итерационный процесс (1.101)–(1.104) со сверхлинейной (локально с квадратичной) скорости сходится к x*S(x₀,r). Теорема доказана.

Теоремы, аналогичные теоремам 1.2-1.5 справедливы относительно процесса (1.101)-(1.103).

Весьма эффективным представителем семейства сверхлинейных многошаговых итерационных процессов, реализующих процедуру неполного прогноза, служит следующий итерационный процесс:

Шаг 1. Решается линейная система для определения поправки

(1.107)

Шаг 2. Находим очередное приближение

. (1.108)

Шаг 3. Если (параметр останова), то конец просчетов, иначе

Шаг 4. Определяется новая шаговая длина, если , то

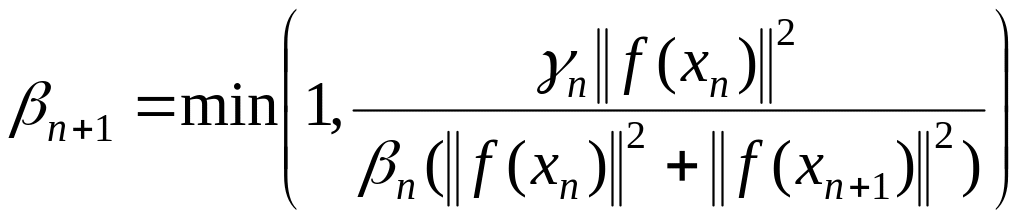; (1.109)

; .

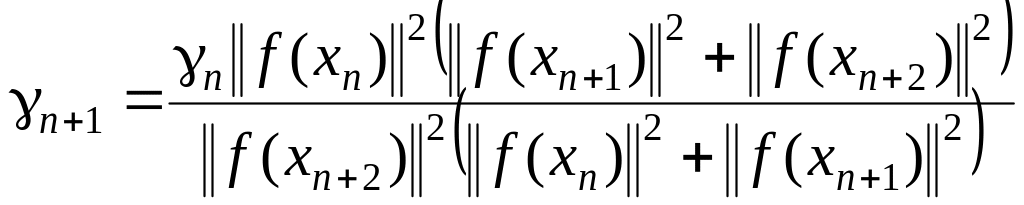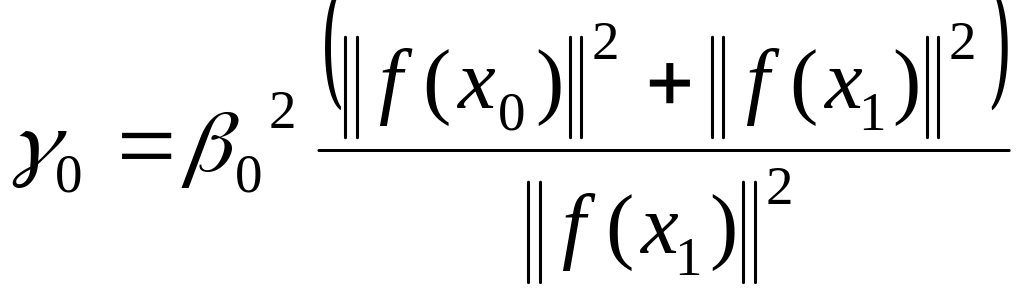Относительно процесса (1.107)-(1.109) справедлива теорема

Теорема 1.19: Пусть в шаре S(x₀,r), , выполняется условие теоремы 1.1. Тогда итерационный процесс (1.107)-(1.109) со сверхлинейной (локально с квадратичной) скоростью сходится к x*S(x₀,r)

Доказательство. Следуя идеям, которые были реализованы выше, найдём связь между шаговыми длинами и нормами невязок.

Пусть , тогда из (1.109) имеем

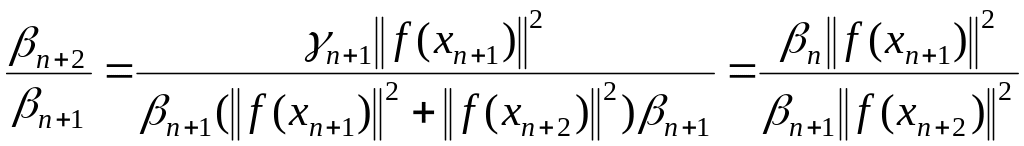. (1.110)

Из (1.110) следует, что справедливо равенство

. (1.111)

Вполне аналогично тому, как это мы делали выше, из условий теоремы и (1.111) имеем, что последовательность норм невязок и последовательность , убывает к нулю, последовательности с чётными и нечётными номерами монотонно возрастают к единице. Покажем, что существует такой номер итерации k, что .

В самом деле, пусть , тогда из (1.109) имеем

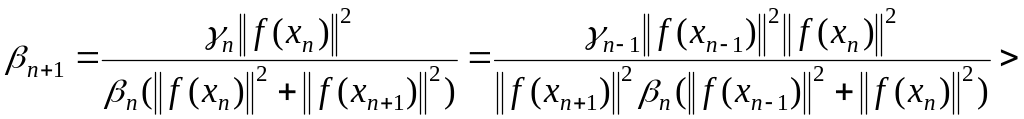(1.112)

.

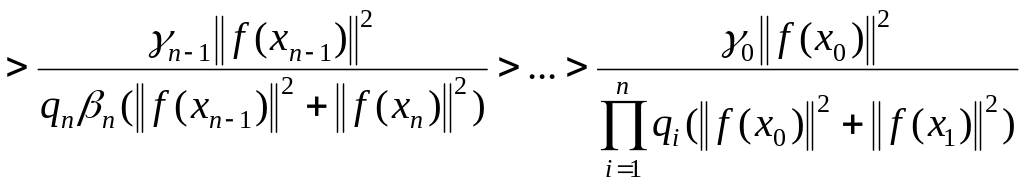В числителе правой части неравенства (1.112) константа, а знаменатель стремится к нулю при , следовательно существует такой номер итерации k, что =1 при . А так как, при , то при некотором номере итерации m

Взяв i=max(k,m), имеем, что, начиная с номера i, начинает выполнятся достаточное условие сходимости метода Ньютона и налицо сверхлинейная сходимость процесса (1.107)–(1.109). Теорема доказана.

Для процесса (1.107)–(1.109) справедливы теоремы, аналогичные теоремам 1.2-1.5.

Среди многошаговых нелокальных процессов достаточно эффективным является следующий:

Шаг 1. Решается линейная система для определения поправки

n=0,1,2,… (1.113)

Шаг 2. Находим очередное приближение

n=0,1,2,…, (1.114)

Шаг 3. Если (параметр останова), то конец просчетов, иначе

Шаг 4. Если , то , иначе

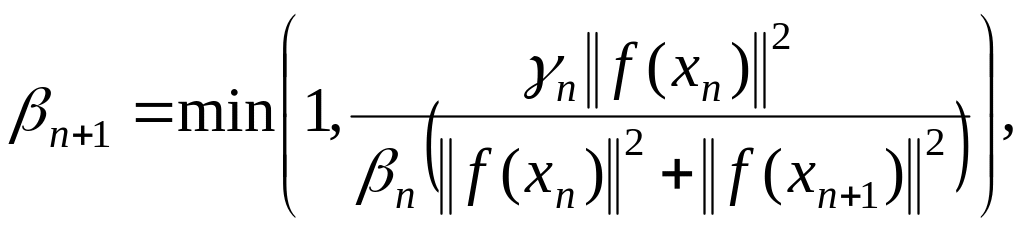(1.115)

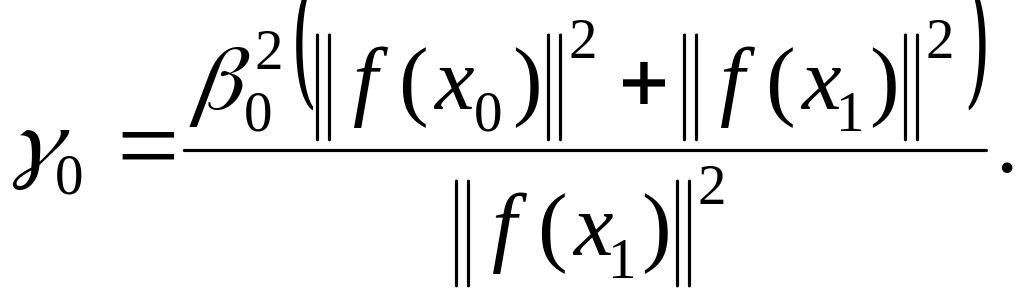
и осуществляется переход на шаг 1.

Относительно процесса (1.113) – (1.115) справедлива

Теорема 1.20. Пусть в шаре выполняются условия теоремы 1.1. Тогда итерационный процесс (1.113) – (1.115) при со сверхлинейной скоростью сходится к . .

Доказательство. Найдем соотношение, связывающее шаговые длины с нормами невязок. Из (1.115) при имеем

. (1.116)

Из (1.116) следует соотношение

(1.117)

Из условий теоремы и (1.117) следует, что последовательность норм невязок монотонно убывает к нулю, шаговые длины с четными и нечетными индексами образуют монотонно возрастающие к единице последовательности.

Пусть , тогда

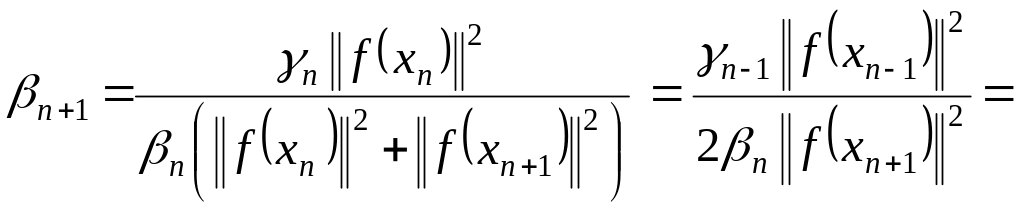
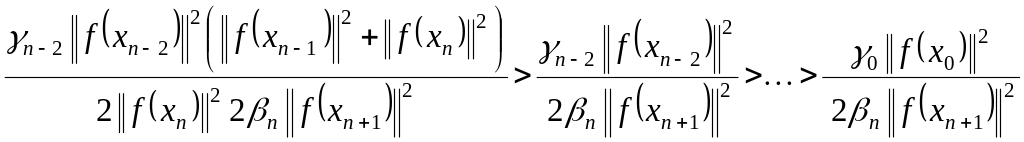. (1.118)

Из (1.118) следует, что при некотором k параметр становится равным единице, а из сходимости последовательности норм невязок к нулю следует, что при некотором номере итерации m выполняется соотношение так что при начинает выполняться достаточное условие сходимости метода Ньютона. Таким образом, итерационный процесс (1.113) – (1.115) со сверхлинейной скоростью сходится к . Теорема доказана.

Относительно процесса (1.113) – (1.115) могут быть сформулированы и доказаны теоремы аналогичные теоремам 1.2. – 1.5.

Рассмотрим следующий способ введения шаговой длины:

.

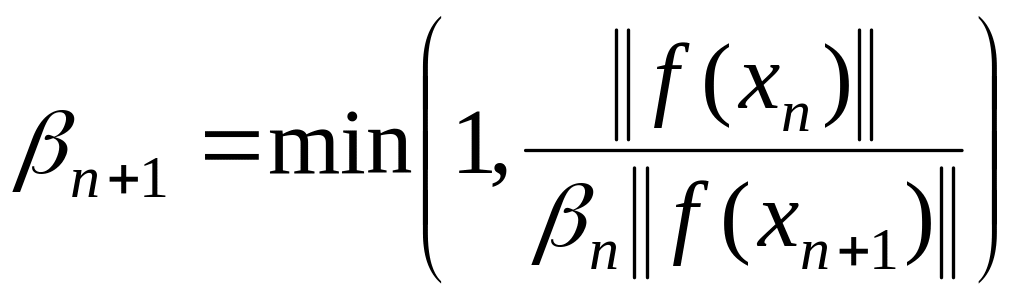Теорема 1.21. Пусть выполняются условия теоремы 1.1 и . Тогда квазиньютоновский итерационный процесс с выбором такой шаговой длины со сверхлинейной скоростью сходится к решению , если такое решение в области D существует.

Доказательство. Если , то имеет место соотношение:

,

откуда следует, что.

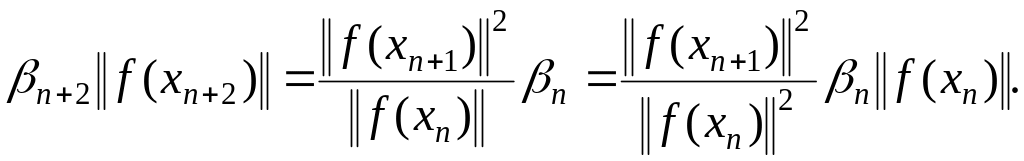
Так как, , то, как показано выше, .

Из способа задания шаговой длины имеем, что ,

.

При из соотношение между шаговыми длинами и нормами невязок следует, что

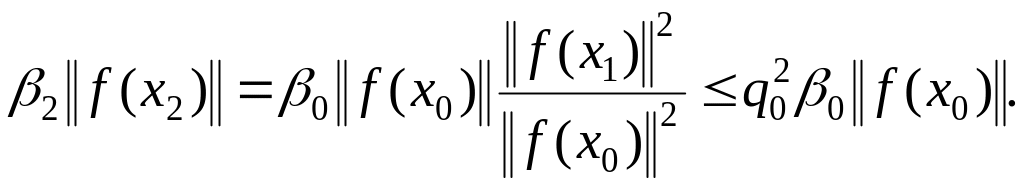
Так как , то, как следует из способа определения шаговой длины, . Из последнего неравенчтва имеем, что

.

А это и есть достаточное условие сходимости метода Ньютона на элементе . Сверхлинейность рассматриваемого выше процесса доказывается стандартным образом. Теорема доказана.

Замечание 6. Рассмотренный выше итерационный процесс чаще пробует осуществить полный ньютоновский шаг и поэтому обладает повышенной скоростью сходимости.

Относительно процессов, рассмотренных в этом параграфе справедливо замечание 1.