2. Регуляризованные итерационные алгоритмы для решения уравнения (1.1) мгнрш
Для «плохих» нелинейных задач с успехом применяются регуляризованные алгоритмы, реализующие процедуру «прогноза-коррекции». Начнем рассмотрение с алгоритмов неполного «прогноза-коррекции».
Шаг 1. Решается линейное уравнение
(1.320)
n=0,1,…
Шаг 2.
(1.321)
Шаг 3.
Если
то конец просчетов, иначе
Шаг 4. Шаговая длина находится по одной из формул (1.301) – (1.309) или по формуле (1.294), далее переход на шаг 1.
Здесь
– оператор, сопряженный оператору
.
В предположении, что существует
ограниченный обратный оператор
,
(1.320) можно переписать в виде
. (1.322)
Используя аналог интерполяционной формулы Ньютона для операторов и (1.320), имеем
(1.323)
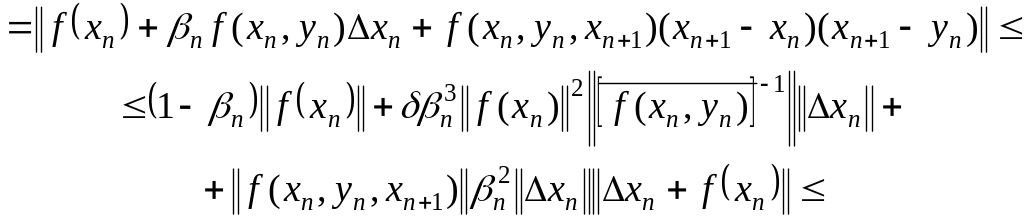
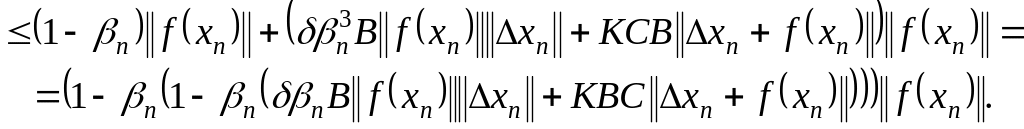
Здесь введены обозначения оценок
,
.
Соотношение
(1.323) является базовым при рассмотрении
различных регуляризованных итерационных
процессов. Если ввести обозначение
,
то за счет малости
,
становится меньше единицы,
и
.
Далее, следуя идеям работ [70, 72, 76], вполне
аналогично тому, как это мы делали выше
при доказательстве теорем 1.53, 1.54,
показываем сверхлинейную сходимость
процессов к
–
решению уравнения (1.1), если это решение
в
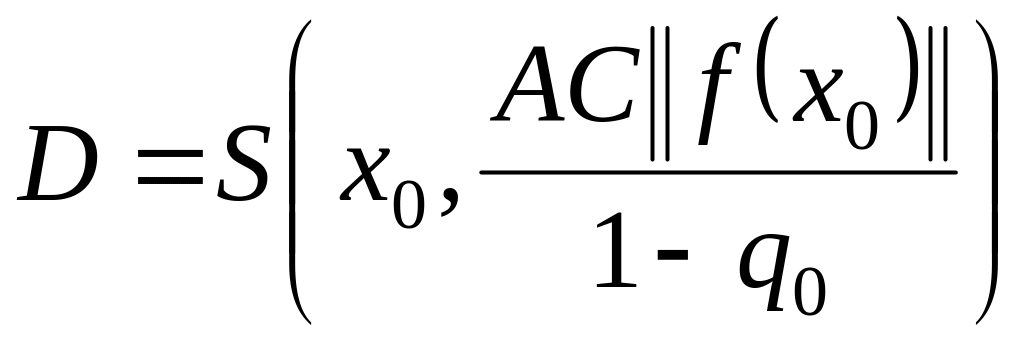существует. Таким образом, могут быть
сформулированы
Теорема
1.57. Пусть в
области
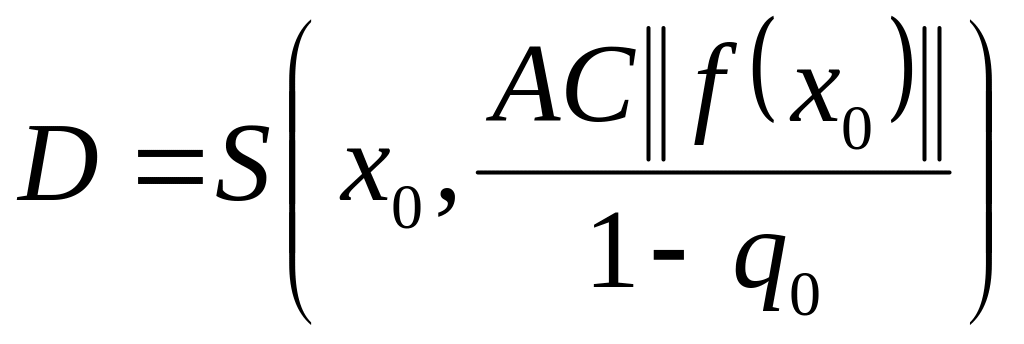существует решение уравнения (1.1). Если
оператор f
удовлетворяет перечисленным выше
условиям и
,
то итерационный процесс (1.320), (1.321) с
,
определенными по формуле (1.294) – (1.296)
или
,
определенными по одной из формул (1.301)
– (1.309) со сверхлинейной скоростью
сходится к
.
Процессы МГНРШ отличаются от МНРШ лишь на шаге 1. Все алгоритмы поиска шаговой длины без изменения могут использоваться в МГНРШ. В случае неполного прогноза МГНРШ переходит в МНРШ.
Замечание 24. При рассмотрении регуляризованных методов нам на каждом шаге вычислительного процесса приходится решать СЛАУ (1.320) с положительно-определенными симметричными матрицами. Специальный вид этих матриц позволяет организовать решение систем (1.320) прямыми методами практически на уровне вычислительных затрат метода Гаусса.
Практическое применение описанных выше регуляризованных алгоритмов показало их высокую эффективность при решении существенно нелинейных задач теории колебаний [78–80].