Билет 19

1.Закономерности целостности систем:коммуникативность, иерархичность.

Коммуникативность: Эта закономерность составляет основу определения системы. Система образует особое единство со средой; любая исследуемая система представляет собой элемент системы более высокого порядка; элементы любой исследуемой системы, в свою очередь, обычно выступают как системы более низкого порядка.

Иерархия - это упорядоченность компонентов по степени важности

Иерархичность как закономерность заключается в том, что закономерность целостности проявляется на каждом уровне иерархии. Благодаря этому на каждом уровне возникают новые свойства, которые не могут быть выведены как сумма свойств элементов. При этом важно, что не только объединение элементов в каждом узле приводит к появлению новых свойств, которых у них не было, и утрате некоторых свойств элементов, но и что каждый член иерархии приобретает новые свойства, отсутствующие у него в изолированном состоянии.

Таким образом, на каждом уровне иерархии происходят сложные качественные изменения, которые не всегда могут быть представлены и объяснены. Но именно благодаря этой особенности рассматриваемая закономерность приводит к интересным следствиям. Во-первых, с помощью иерархических представлений можно отображать системы с неопределенностью.

Во-вторых, построение иерархической структуры зависит от цели: для многоцелевых ситуаций можно построить несколько иерархических структур, соответствующих разным условиям, и при этом в разных структурах могут принимать участие одни и те же компоненты. В-третьих, даже при одной и той же цели, если поручить формирование иерархической структуры разным исследователям, то в зависимости от их предшествующего опыта, квалификации и знания системы они могут получить разные иерархические структуры, т. е. по-разному разрешить качественные изменения на каждом уровне иерархии.

2.Модель системы в виде графа (матрица смежности,матрица изоморфности).

Графы используются для описания алгоритмов автоматического проектирования и при решении задач маршрутизации потоков.Соединение между узлами графов называется рёбрами.Граф представляет собой структуру, в которой V-конечный набор узлов,а Е- конечныё набор рёбер. Рёбра не могут иметь общих точек, кроме вершин графа. G=<V,E> E=V*V. Если V и Е конечное число, то граф конечный.Граф называется вырожденным, если он не имеет рёбер. Параллельные ребра, такие рёбра, которые имеют общие узлы начала и конца. Граф G плоский, если его можно отоброзить в плоскости без пересечения граней. Очертанием графа считается любая топологически связная область ограниченная рёбрами графа. Неориентированный граф называется связным, если для любых двух узлов х,у принадлежащих V, существует последовательность рёбер из набора E соединяющи х и у. Граф G связан тогда и только тогда, когда множество его вершин нельзя разбить на два пустых подмножества V₁ и V₂, так чтобы обе граничные точки каждого ребра находились в одном и том же подмножестве. Граф G является к-связным тогда и только тогда, когда любые х и у, соединены, по крайней мере, к путями, не содержащими общих узлов. Число рёбер исходящих из вершин с нечётной степенью всегда чётно. Граф называется обыкновенным, если он не содержит петель и параллельных рёбер. Граф называется полным, если любые две вершины являются смежными. Если для всех вершин G(V)=к, то граф называется однородным графом степени к .Конечную последовательность рёбер графа l₁...l_n называют маршрутом. Маршрут называется замкнутым, если вершина начала и конца маршрута совпадает. Если рёбра образующие маршрут различны, то такой маршрут называют цепью. Граф называется деревом, если он связан и не имеет циклов. Граф является деревом тогда и только тогда, когда каждая пара различных вершин соединена одной и только одной цепью. Каждое дерево с n вершинами имеет n-1 ребро. Удаление любого ребра делает граф не связным. Дерево – минимальный связный граф.

Поиск контуров и путей по матрице смежности

Наиболее простым способом идентификации путей и контуров являются матричные алгоритмы структурного анализа. Они строятся на основе последовательного возведения в соответствующие степени матрицы смежности. Единица в матрице смежности S говорит о наличии пути между i‑й и j-й вершинами длиной 1. Наличие 1 в (i, j)-й позиции в матрицы 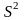означает путь длиной 2 между этими вершинами, и так далее. Таким образом, существование ненулевого значения на главной диагонали означает наличие пути из дан­ной вершины в данную вершину, длинна которого равна степени матрицы. Наличие 1 в главной диагонали указывает на то, что четыре переменные сис­темы входят в контуры длиной 2. Это позволяет определить вершины, вхо­дящие в контуры, его длину, но не конкретный вид. Поэтому требуется уточняющий переборный алгоритм на отобранных вершинах нелинейного системного гибридного графа, определя­ющего конкретный вид контура известной длины. Четвертая степень матрицы смежности 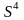содержит информацию об еще одном контуре длиной 4. Но кроме этого повторяется информация о кон­турах длиной 2. Отмеченные особенности этого метода, повторение ин­формации о контурах в матрицах более высокого порядка, кратного длине контура; трудности в обработки контуров одинаковой длины, требуют применения, в дополнению к рассматриваемому методу переборного алгоритма, уточняющего и отбрасывающего повторяющую информацию. Наиболее существенным недостатком данного метода является его низкое быстродействие в следствие большого количества возведений матрицы смежности в соответствующие степени и большие затраты памяти ЭВМ для хранения информации.

Модифицированный алгоритм поиска контуров и путей по матрице смежности

Недостатки алгоритма поиска путей и контуров на основании представления топологии модели в форме матриц смежности, отмеченные выше, могут быть компенсированы, если использовать логические операции вместо математических и побитовое представление матрицы смежности. Быстрый рост необходимой памяти и временных затрат на работу алгоритма с ростом размерности систем в предлагаемом алгоритме компенсируются иерархическим представлением топологии модели а так же иерархическим характером построения алгоритмов топологического анализа. Реализация алгоритма в этом случае использует не умножение, а логическую операцию И (в матрице присутствуют только значения 0 и 1), выполняемую одной машинной командой.Как отмечалось ранее, составной характер представляемых моделей требует учета наличия связей между входами и выходами внутри подсистем. С этой целью водится матрица существования связи:

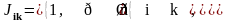
Логическая сумма, - операции ИЛИ - позволяет определить все возмож­ные связи между вершинами. 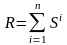где n - размерность системы и, кроме того, определяет длину макси­мально возможного пути. Данную сумму называют матрицей достижимости. Транспонированная матрица достижимости называемой матрицей контрдостижимостей.

Если в матрице достижимости оставить только входные и выходные вершины подсистемы данного уровня иерархии, то получится матрица связей J , которая должна быть передана в вышестоящую по уровню систему для составления аналогичных функций структур­ного анализа и учета этой информации на стадии моделирования.

Поиск контуров и путей по матрице изоморфности

6. 5. Диаграмма графа

Матрица изоморфности

-1 7

-2 1 6

-3 2

3 5 -4

4 -8

8 -5 -6 -9

9 -7

Алгоритм идентификации контуров следующий:

Просмотреть строки матрицы. Для i-й строки просмотреть элементы до обнаружения отрицательного элемента D_{i j} <0. Запомнить номер строки и значение элемента D_{i j}.Найти строки в матрице содержащие элемента D _{k l} == - D_{i j}. Для каждой найденной строки выполнить пп. 1, до тех пор пока в найденной последовательности повторно не вертится уже обнаруженная дуга, или программе не удастся обнаружить новую дугу, выходящую из этой вершины.

В 0-й строке нашел D[0][0]= -1 ;Нашел D[1][1]= 1 ; В 1-й строке нашел новый отрицательный элемент D[1][0] = -2 ;Нашел D[2][1]= 2 ;В 2-й строке нашел новый отрицательный элемент D[2][0] = -3 ;Нашел D[3][0] = 3 ;В 3-й строке нашел новый отрицательный элемент D[3][2] = -4 ;Нашел D[4][0]= 4 ; В 4-й строке нашел новые отрицательные элементы D[4][1] = -5, D[4][1] = -6, D[4][1] = -9. Необходимо разветвить поиск ; Нашел D[3][1]= 5 ;В 3-й строке нашел отрицательный элемент D[3][2] = -4. Этот элемент уже был в цепочки поиска. Поиск по этой ветки прекращен. Возвращаемся в пп.9 ;Нашел D[1][2]= 6 ;В 1-й строке нашел отрицательный элемент D[1][0] = -2. Этот элемент уже был в цепочки поиска. Поиск по этой ветки прекращен. Возвращаемся в пп.9 ;Нашел D[6][0]= 9 ;В 6-й строке нашел новый отрицательный элемент D[6][1] = -7 ;Нашел D[0][1]= 7 ;В 0-й строке нашел D[0][0]= -1. Этот элемент уже был в цепочки поиска. Поиск по этой ветки прекращен.Новых отрицательных элементов в матрице не осталось поиск прекращен. После завершения поиска имеем:

-1 -2 -3 -4 -8 -5 -4

-6 -2

-9 -7 -1