
- •Вопрос 1. Определение множества
- •1.1.2. Операции над множествами
- •1.1.3. Свойства операций над множествами
- •1.2. Функции, их классификация
- •1.3. Предел последовательности
- •Вопрос4
- •Односторонние пределы. Необходимое и достаточное условия существования предела функции
- •Вопрос 6. Бесконечно малые и бесконечно большие функции
- •Вопрос 7. Теоремы о представлении функции в виде суммы предела и бесконечно малой функции
- •Вопрос8 Первый замечательный предел
- •Вопрос 9. Второй замечательный предел
- •1.8.3. Применение второго замечательного предела в финансовых вычислениях
- •Вопрос 10.Сравнение бесконечно малых функций
- •Вопрос 11.Непрерывность функции в точке и на отрезке.
- •Вопрос 12.Свойства непрерывных функций
- •Вопрос 13.Точки разрыва функций
- •Вопрос14.Определение производной функции
- •Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •Вопрос 16.Вывод производных основных элементарных функций
- •Правила дифференцирования
- •2.1.9. Производные высших порядков
- •Вопрос 20. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •Вопрос 22. Применение дифференциала для приближенных вычислений
- •Вопрос 23.Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •24. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •Вопрос 27. Формула Тейлора. Остаточный член в форме Лагранжа
- •Вопрос 28. Формула Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •Вопрос 31. Определение экстремума функции
- •Вопрос 32.Первый достаточный признак экстремума функции (с использованием первой производной)
- •34. Необходимый признак существования точки перегиба
- •35.Асимптоты графика функции
- •2.5.11. Построение графика функции
- •3.4. Свойства пределов
- •38.Бесконечно малые функции нескольких переменных
- •47. . Производная функции по направлению
2.3.3. Примеры использования теоремы Ролля
Рассмотрим три функции.
1.
Функция
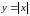 является непрерывной на отрезке [1;
1] и принимает равные значения в граничных
точках
является непрерывной на отрезке [1;
1] и принимает равные значения в граничных
точках
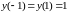 .
Однако функция не имеет производной в
точке х
= 0, так как при х
> 0
.
Однако функция не имеет производной в
точке х
= 0, так как при х
> 0
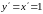 ,
а при х
< 0
,
а при х
< 0
 .
Нарушение условия дифференцируемости
функции только в одной внутренней точке
отрезка приводит в данном случае к
отсутствию точки, в которой производная
функции равна нулю, а касательная к
графику горизонтальна (рис. 24).
.
Нарушение условия дифференцируемости
функции только в одной внутренней точке
отрезка приводит в данном случае к
отсутствию точки, в которой производная
функции равна нулю, а касательная к
графику горизонтальна (рис. 24).
3.
Функция
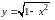 на
отрезке [1;
1] удовлетворяет всем требованиям теоремы
Ролля. Функция является непрерывной на
отрезке [1;
1], принимает равные значения в граничных
точках отрезка
на
отрезке [1;
1] удовлетворяет всем требованиям теоремы
Ролля. Функция является непрерывной на
отрезке [1;
1], принимает равные значения в граничных
точках отрезка
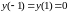 и ее производная
и ее производная
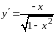 существует в каждой внутренней точке
отрезка. В граничных точках отрезка
производная не существует (бесконечная).
В теореме Ролля не требуется
дифференцируемости функции в граничных
точках отрезка. Всего этого достаточно,
чтобы существовала внутренняя точка
отрезка х
= 0, в которой производная равна нулю, а
касательная параллельна оси Ох
(рис. 26).
существует в каждой внутренней точке
отрезка. В граничных точках отрезка
производная не существует (бесконечная).
В теореме Ролля не требуется
дифференцируемости функции в граничных
точках отрезка. Всего этого достаточно,
чтобы существовала внутренняя точка
отрезка х
= 0, в которой производная равна нулю, а
касательная параллельна оси Ох
(рис. 26).
24. Теорема Лагранжа о конечном приращении функции
Теорема
Лагранжа.
Если функция
непрерывна на отрезке
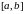 и дифференцируемая в каждой его внутренней
точке, то на интервале (a,
b)
найдется такая точка х
= с,
что
и дифференцируемая в каждой его внутренней
точке, то на интервале (a,
b)
найдется такая точка х
= с,
что
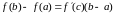 .
.
2.3.5. Геометрический смысл теоремы Лагранжа
На
основании формулы
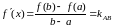 можно утверждать следующее.
можно утверждать следующее.
Рис. 28 |
Если
график функции y
= f(x)
непрерывный на отрезке
и гладкий на интервале
|
2.3.6. Теорема Коши
Теорема
Коши. Если
функции y
= f(x)
и y
= g(x)
непрерывные на отрезке
,
дифференцируемые в каждой внутренней
точке этого отрезка и при этом производная
y
= g(x)
ни в одной из этих точек не обращается
в нуль (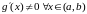 ),
то найдется такая внутренняя точка
,
что
),
то найдется такая внутренняя точка
,
что
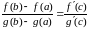 .
.
Д
о к а з а т е л ь с т в о. Очевидно, что
 ,
иначе по теореме Ролля существовала бы
такая точка
,
в которой
,
иначе по теореме Ролля существовала бы
такая точка
,
в которой
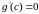 ,
что противоречит условию теоремы.
,
что противоречит условию теоремы.
Составим вспомогательную функцию y = F(x), которая будет удовлетворять условиям теоремы Ролля.
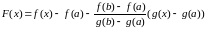 .
.
Значения функции y = F(x) в точках х = а и х = b равны нулю. Действительно,
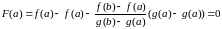 ,
,
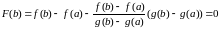 .
.
Функция y = F(x) является дифференцируемой, так как является линейной комбинацией дифференцируемых функций y = f(x) и y = g(x). Находим
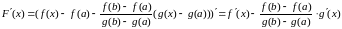 .
.
По теореме Ролля существует точка , в которой производная функции y = F(x) равняется нулю
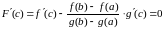 .
.
Отсюда получаем
.
2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
Теорема
2.1. Если в
некоторой окрестности точки
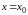 функции y
= f(x)
и y
= g(x)
определены и дифференцируемые, причем
функции y
= f(x)
и y
= g(x)
определены и дифференцируемые, причем
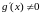 ,
пределы функций при
,
пределы функций при
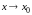 равны нулю, т. е.
равны нулю, т. е.
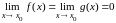 ,
то предел отношения этих функций
равняется пределу отношения их производных
,
то предел отношения этих функций
равняется пределу отношения их производных
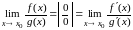 ,
,
если этот предел существует (конечный или бесконечный).
Правило
Лопиталя справедливо также в случае
когда
 .
Покажем
.
Покажем
Правило
Лопиталя справедливо так же, если
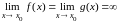 ,
т. е имеет место неопределенность типа
,
т. е имеет место неопределенность типа
 ,
,
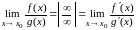 .
.
Пример
2.10.
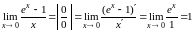 .
.
Если
при нахождении пределов неопределенность
имеет вид произведения
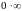 ,
то прежде, чем применять правило
Лопиталя, ее нужно привести к
неопределенностям типа частного
,
то прежде, чем применять правило
Лопиталя, ее нужно привести к
неопределенностям типа частного
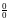 или
или
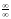 .
.
Пример
2.13.
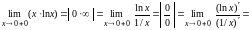
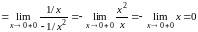 .
.
Если при применении правила Лопиталя под пределом имеются некоторые функции, которые не приводят к неопределенности, то эти функции нужно выделить в отдельный предел, т. е. разбить предел на два предела.
Пример 2.15.
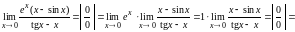
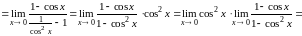
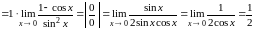 .
.
Применение правила Лопиталя для раскрытия неопределенностей типа степени
Если
при нахождении пределов имеет место
неопределенность типа степени вида
 ,
то ее необходимо привести к неопределенности
типа частного. Пусть имеет место
неопределенность типа степени при
нахождении предела
,
то ее необходимо привести к неопределенности
типа частного. Пусть имеет место
неопределенность типа степени при
нахождении предела
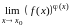 .
Используем определение логарифма,
преобразуем данный предел
.
Используем определение логарифма,
преобразуем данный предел
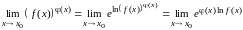 .
.
Так как показательная функция является непрерывной, то можно перейти к пределу в показателе степени, т. е.
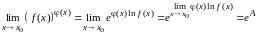 .
.
При
нахождении предела
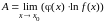 неопределенность имеет тип произведения,
которую необходимо свести к неопределенности
типа частного.
неопределенность имеет тип произведения,
которую необходимо свести к неопределенности
типа частного.
Пример
2.16.
 .
.
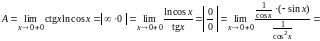
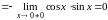 .
.
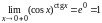 .
.

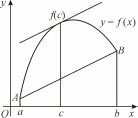
 ,
то на этом интервале найдется такая
точка
,
то на этом интервале найдется такая
точка
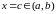 ,
в которой касательная параллельна
хорде, стягивающей граничные точки
графика функции (рис. 28).
,
в которой касательная параллельна
хорде, стягивающей граничные точки
графика функции (рис. 28).