2.  

Линейная комбинация векторов 

     Линейной комбинацией векторов   называют вектор

     

где   - коэффициенты линейной комбинации. Если   комбинация называется тривиальной, если   - нетривиальной.

     Линейная зависимость и независимость векторов 

     Система   линейно зависима     что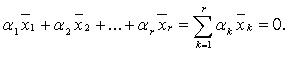 

     Система   линейно независима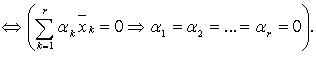 

     Критерий линейной зависимости векторов 

     Для того чтобы векторы   (r > 1) были линейно зависимы, необходимо и достаточно, чтобы хотя бы один из этих векторов являлся линейной комбинацией остальных.

3. Координаты вектора. Замена базиса и преобразование координат.

Если система векторов e₁, ..., e_n n-мерного линейного пространства L_n образует базис в L_n, то любой вектор x из L_n может быть представлен в виде

x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n.

Выражение x = С₁·e₁+ С₂·e₂+ ...+ С_n· e_n называется разложением вектора по базису e₁, ..., e_n, а числа С₁, С₂, ..., С_n называются координатами вектора x  в базисе e₁, ..., e_n.

Координаты вектора принято обозначать тем же символом, что и сам вектор:

x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n.

Взаимно однозначное соответствие x = x₁·e₁+ x₂·e₂+ ...+ x_n· e_n ⇐⇒ x = (x₁, x₂, ..., x_n)

— изоморфизм L_n и R_n.

Пусть системы векторов e = {e₁, ..., e_n} и f = {f₁, ..., f_n} — два базиса n-мерного линейного пространства L_n.

Обозначим x_e = (x₁,x₂, ..., x_n) и x_f = (x'₁,x'₂, ..., x'_n) — координаты вектора x ∈ L_n соответственно в базисах e и f.

Справедливо следующее x_e= C_e→f·x_f :

Здесь C_e→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f₁, ..., f_n  в базисе  e₁, ..., e_n:

f₁ = с₁₁· e₂ + с₂₁· e₁ + ... + с_n1· e_n, f₂ = с₁₂· e₁ + с₂₂· e₂ + ... + с_n2· e_n, ..., f_n = с_1n· e₂ + ... + с_nn· e_n.

Формулу преобразования координат вектора при изменении базиса принято записывать в виде

x_f= (C_e→f)^{− 1}·x_e

Пример!!!!!!!

Вектор x = (−1, 0, 5) задан своими координатами в базисе e = {e₁, e₂, e₃}.

Найдем координаты вектора x в базисе  f = {f₁, f₂, f₃} , где

Матрица C_e→f перехода от базиса e к базису f и обратная к ней матрица (C_e→f)^{− 1} имеют вид:

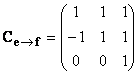
Тогда

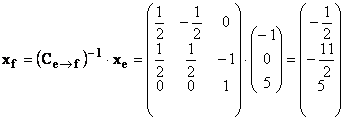
4. Подпространства. Сумма и пересечение подпространств.

Определение. Непустое подмножество   линейного пространства   называется подпространством, если   для любых векторов   и   .

Замечание. В любом пространстве содержится нулевое подпространство   (самое маленькое). Пространство   самое большое. Если   , то   и   . Если  и   , то   .

Теорема. Пусть   и   подпространства конечномерного пространства   , причем  . Тогда   и из равенства размерностей следует равенство подпространств   .

Определение. Пусть   ,   . Линейной оболочкой   системы  называется множество значений всевозможных линейных комбинаций   , где  . Линейная оболочка пустого множества -- это нулевое подпространство.

Теорема.   Линейная оболочка   является подпространством пространства   .

Множество K векторов из линейного пространства L называется линейным подпространством пространства L , если сумма x + y любых двух векторов x и y из L принадлежит K и произведение α·x любого любого числа α и любого вектора x и y из L принадлежитK:

Пересечение линейных подпространств

Лемма 9.11.1. Пересечение

любого семейства линейных подпространств   линейного пространства _K V является линейным подпространством.

Доказательство. Если  ,  , то   для любого  , поэтому   для любого  , т. е.  .

Следствие 9.11.2. Если U₁ и U₂ - линейные подпространства линейного пространства _K V, то   - линейное подпространство в {_K V (наибольшее подпространство среди подпространств, лежащих одновременно в U₁ и в U₂ ).

5. Размерность суммы и пересечения подпространств.

СУММА

Пересечение

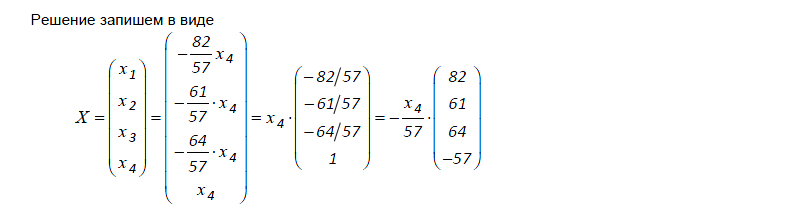
Формулу Грассмана можно использовать для нахождения размерности пересечения подпространств

6.Скалярно произведение векторов в ортонормированном и произвольном базисе. Понятие евклидова и унитарного пространства.

Скалярное произведение.

Определение Ошибка! Текст указанного стиля в документе отсутствует..1. Скалярным произведением геометрических векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение векторов обозначают .

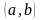Длина вектора равна .

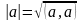Приведём свойства скалярного произведения.

1. . Симметричность

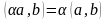2. Линейность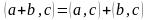

3. 

Ортогональный базис , в котором длина каждого базисного вектора равна 1, называется ортонормированным. В ортонормированном базисе координаты вектора x определяются по формулам 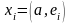, а скалярное произведение векторов равно .

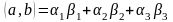Рассмотрим, как изменится выражение для скалярного произведения, записанное через их координаты в произвольном базисе. Итак, пусть   – произвольный базис,    и    – любые два вектора. Рассмотрим скалярное произведение этих векторов и преобразуем его, используя ранее доказанные свойства:     

Таким образом, для вычисления скалярного произведения двух векторов в произвольном базисе, кроме их координат, надо знать модули базисных векторов и угол между ними. Очевидно, что если базис ортонормирован, то        и мы получим известную формулу для скалярного произведения в ортогональной декартовой системе координат.

Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.

Пусть V линейное пространство над полем комплексных чисел. Можно ли обобщить понятие скалярного произведения на такое пространство. Оказывается, да! Для этого достаточно незначительно изменить аксиомы скалярного произведения.

1. .

2. 

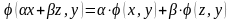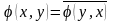
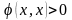3. при .

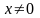Черта в свойстве 2 обозначает знак комплексного сопряжения. Пространство над полем комплексных чисел, в котором введено скалярное произведение называется унитарным.

7. Матрица Грама.

Матрицей Грама системы векторов a1…ak называется матрица на пересечении строки i столбца j стоит скалярное произведение i-го и j-го вектора 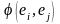.  Теорема. Система векторов линейно зависима тогда и только тогда, когда определитель Грама равен нулю. Док-во. Рассмотрим вектор, являющийся линейной комбинацией векторов системы: y = α1a1 + α2a2..+αkak – равенство его нулю равносильно ортогональности каждому вектору оболочки, натянутой на векторы a1..ak – это равносильно ортогональности каждому вектору системы. Записываем эти условия в систему и получаем, что это выполняется тогда и только тогда, когда определитель матрицы нулевой. Теорема. Матрица Грама системы векторов евклидова (ун) пространства эрмитова. Док-во. Транспонируем, сопрягаем, получаем тож самое. Доказано. Теорема. Определитель Грама линейно независимой системы векторов положителен. Док-во. Пусть а1..аk - лнз система векторов. Выберем ортонормированный базис е1..еk, составим матрицу координат а1..ak в этом базисе, матрица Грама равна (A'A)т, определитель матрицы Грама равен квадрату определителя матрицы А - то есть положителен.

Свойство Ошибка! Текст указанного стиля в документе отсутствует..1. Матрица Грама ортогональной системы векторов – диагональная.