
- •Пересечение линейных подпространств
- •Скалярное произведение.
- •Для ортонормированных векторов матрица Грама – единичная
- •8. Ортогонализация совокупности векторов.
- •18. Характеристический и минимальный полином. Теоремам Гамильтона-Кели.
- •19. Собственные значения и собственные векторы линейного оператора.
- •Нормальный вид квадратичной формы
Для ортонормированных векторов матрица Грама – единичная
8. Ортогонализация совокупности векторов.
процесс ортогонализации,- алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, порождающих то же самое подпространство в V. Наиболее известным является процесс ортогонализации Шмидта (или Грама - Шмидта), при к-ром по линейно независимой системе al,...,akстроится ортогональная система bl,...,bk такая, что каждый вектор bi (i=1,...,k).линейно выражается через al,...,ai
Полагают b1 = a1, и, если уже построены векторы b1,b2,..,bi − 1, то
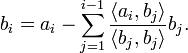
Геометрический смысл описанного процесса состоит в том, что на каждом шагу вектор bi является перпендикуляром, восстановленным к линейной оболочке векторов a1,...,ai − 1 до конца вектора ai.
9.Подпространства евклидова(унитарного) пространства.
10. Ортогональное дополнение и ортогональная проекция. Прямая сумма подпространств.
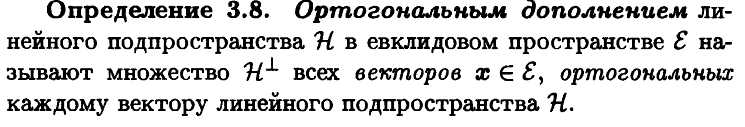

 Говорят,
что линейное
пространство
Говорят,
что линейное
пространство ![]() есть прямая
сумма своих подпространств
есть прямая
сумма своих подпространств ![]() :
:
![]()
если
каждый вектор ![]() представляется
в виде суммы
представляется
в виде суммы
![]()
и притом единственным образом.
Комментарий
Последнее
условие («единственным образом») весьма
существенно, без него получается просто
определение суммы подпространств
(обозначается ![]() ).
Из определения линейного пространства
следует, что условие единственности
разложения (*) для
каждого вектора
равносильно
условию единственности разложения (*)
только для
нулевого вектора (для
).
Из определения линейного пространства
следует, что условие единственности
разложения (*) для
каждого вектора
равносильно
условию единственности разложения (*)
только для
нулевого вектора (для ![]() в
сумме (*) все слагаемые
в
сумме (*) все слагаемые ![]() ).
).
Критерии прямой суммы
Каждый вектор раскладывается в сумму (*), причём
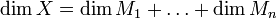 (Если
конечномерно)
(Если
конечномерно)Любая система из
 ненулевых
векторов, принадлежащих различным
подпространствам, линейно
независима.
ненулевых
векторов, принадлежащих различным
подпространствам, линейно
независима.Пересечение каждого из подпространств
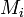 с
суммой остальных есть нулевое пространство
(пространство, состоящее только из
нулевого вектора).
с
суммой остальных есть нулевое пространство
(пространство, состоящее только из
нулевого вектора).Если линейное пространство обладает базисом, то объединение базисов подпространств
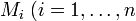 )
есть базис в
.
)
есть базис в
.
11. Линейные многообразия. Задание линейных

Решения любой совместной системы линейных уравнений с n неизвестными ранга r образуют линейное многообразие пространства Rn размерности d=n-r и обратно
Линейное пространство путем параллельного сдвига образует линейное многообразие.
12. Расстояние от точки до линейного многообразия.
Расстоянием от точки, заданной вектором х, до линейного многообразия Р=L+x0 называется минимум расстояний от данной точки до точек многообразия, то есть минимум длин векторов x-u, где u-вектор многообразия P.
Расстояние равно длине ортогональной составляющей z вектора x-x0 относительно линейного подпространства L, параллельным сдвигом которого получатся многообразие P.
13. Расстояние между многообразиями.
Расстоянием между двумя линейными многообразиями Р1=L1+x1 и P2=L2+x2 называется минимум расстояний любых двух точек, одна из которых принадлежит P1 , а другая Р2 .
Расстояние равно длине ортогональной составляющей вектора
x1-x2 относительно линейного подпространства L=L1+L2
14. Ортонормированный базис. Преобразование координат при ортонормированном базисе.
Ортонормированная система, состоящая из n векторов n-мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.
Если e1, e2, ..., en — ортонормированный базис n-мерного евклидова пространства и
x = x1e1 + x2e2 + ... + xnen — разложение вектора x по этому базису, то координаты xi вектора x в ортонормированном базисе вычисляются по формулам xi =(x, ei), i = 1, 2, ..., n.
15. Линейное отображение векторного пространства. Примеры.
Лине́йным
отображе́нием векторного
пространства ![]() над полем
над полем ![]() в
векторное пространство
в
векторное пространство ![]() (лине́йным
опера́тором из
в
)
над тем же полем
называется отображение
(лине́йным
опера́тором из
в
)
над тем же полем
называется отображение
![]() ,
,
удовлетворяющее условию линейности
![]() ,
,
![]() .
.
для
всех ![]() и
и ![]() .
.
Пример
1. Нулевое линейное отображение ![]() ,
заданное правилом
,
заданное правилом ![]() для
всех
для
всех ![]() .
.
Пример
2. Тождественное линейное отображение ![]() задается
формулой
задается
формулой ![]() для
всех
для
всех ![]() .
.
Пример
3. Отображение ![]() векторного
пространства
векторного
пространства ![]() из примера
4 в
одномерное вещественное пространство
из примера
4 в
одномерное вещественное пространство ![]() ,
является линейным отображением векторных пространств.
,
является линейным отображением векторных пространств.
16. Матрица линейного оператора. Преобразование матрицы оператора при переходе к новому базису.
Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .
В этих пространствах определены базисы e = {e1, ..., en} и f = {f1, ..., fm}.
Пусть A(ei ) = a1i·f1 + a2i·f2 + ...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису fпространства Y, i = 1, 2, ..., n.
Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {aij}= {A(ej )i}:

Координаты образа y = A(x) и прообраза x связаны соотношеннием:
y = A· x,
![]()

Пусть
V
– линейное пространство, А
– линейный оператор из
![]() ,
,
![]() и
и
![]() –
два базиса в V
и
–
два базиса в V
и
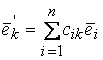 –
формулы перехода от базиса
–
формулы перехода от базиса
![]() к
базису
к
базису
![]() .
Обозначим через
.
Обозначим через
![]() матрицу
перехода от базиса к базису. Отметим,
что ранг матрицы С
равен n.
Пусть
матрицу
перехода от базиса к базису. Отметим,
что ранг матрицы С
равен n.
Пусть
![]() и
и
![]() –
матрицы оператора А
в
указанных базисах.
–
матрицы оператора А
в
указанных базисах.
Теорема
7.1.
Матрицы
А
и
![]() оператора
А
в базисах
и
связаны
соотношением
оператора
А
в базисах
и
связаны
соотношением
![]() .
.
Доказательство.
При
воздействии линейного оператора А
вектор
![]() пространства
пространства
![]() переводится
в вектор
переводится
в вектор
![]() этого
пространства, т.е. справедливо равенство
этого
пространства, т.е. справедливо равенство
= А (7.3)
(в старом базисе) и равенство
![]() =
А
=
А
![]() (7.4)
(7.4)
(в новом
базисе). Так как
![]() –
матрица перехода от старого базиса к
новому, то
–
матрица перехода от старого базиса к
новому, то
![]() (7.5)
(7.5)
![]() (7.6)
(7.6)
Умножим
равенство (7.5) слева на матрицу
![]() ,
получим А
=
АC
и
с учетом (7.3)
=
АC
.
Заменив левую часть полученного выражения
в соответствии с (7.6), получим: С
=
АC
или
=
С–1
АC
.
Сравнивая найденное выражение с
равенством (7.4), получим доказываемую
формулу.
,
получим А
=
АC
и
с учетом (7.3)
=
АC
.
Заменив левую часть полученного выражения
в соответствии с (7.6), получим: С
=
АC
или
=
С–1
АC
.
Сравнивая найденное выражение с
равенством (7.4), получим доказываемую
формулу.
Отсюда следует, что определитель матрицы линейного оператора не зависит от базиса.
17.Действия над линейными операторами. Обратный оператор.
Пусть А
и В –
два линейных оператора, действующих
из V в W. Суммой этих
операторов назовем оператор А + В,
определяемый равенством (А + В)![]() А
А![]() +В
для
любого
из V.
Легко видеть, что сумма линейных
операторов тоже будет линейным оператором.
+В
для
любого
из V.
Легко видеть, что сумма линейных
операторов тоже будет линейным оператором.
Сложение линейных операторов обладает, очевидно, следующими свойствами:
1. А + В = В +А.
2. (А +В) +Е = А + (В + Е).
3. А + О = А для любого А.
4. (–А) + А = О.
Произведением
линейного оператора на
скаляр α
назовем оператор αА,
определяемый равенством ![]() А)
А)![]() А
А![]() .
Ясно, что αА –
тоже линейный оператор.
.
Ясно, что αА –
тоже линейный оператор.
Для умножения линейного оператора на число справедливы, очевидно, следующие свойства:
1. ![]() А = А;
0А = О;
(–1)А= –А.
А = А;
0А = О;
(–1)А= –А.
2. ![]() βА)
βА) ![]() А.
А.
3. ![]() А =
А = ![]() А + βА.
А + βА.
4. (А + В) = А + В.
Обозначим
через ![]() множество
всех линейных операторов, действующих
из V в W.
множество
всех линейных операторов, действующих
из V в W.
Произведением линейных операторов А и В из называется оператор АВ, определяемый следующим образом: (А В) А(В для любого из V. Произведение линейных операторов тоже будет линейным оператором.
Справедливы следующие свойства умножения линейных операторов:
1. АВ) = ( А )В.
2. (АВ)Е = А (ВЕ).
3. (А + В)Е = АЕ + ВЕ, Е(А + В) = ЕА + ЕВ.
Умножение линейных операторов, вообще говоря, некоммутативно.
Линейный
оператор В
из
![]() называется
обратным
для оператора А
из
,
если выполняется соотношение АВ
=
ВА
=
Е.
Обратный оператор обычно обозначается
как А–1.
Для того чтобы линейный оператор А
из
имел
обратный, необходимо и достаточно, чтобы
он был невырожденным.
называется
обратным
для оператора А
из
,
если выполняется соотношение АВ
=
ВА
=
Е.
Обратный оператор обычно обозначается
как А–1.
Для того чтобы линейный оператор А
из
имел
обратный, необходимо и достаточно, чтобы
он был невырожденным.
Будем
говорить, что линейный оператор А
действует взаимно
однозначно
из V
в V,
если любым двум различным элементам
![]() и
и
![]() отвечают
различные элементы
отвечают
различные элементы
![]() А
и
А
и
![]() А
.
Для того чтобы линейный оператор А
из
имел
обратный, необходимо и достаточно, чтобы
этот оператор действовал взаимно
однозначно из V
в V.
А
.
Для того чтобы линейный оператор А
из
имел
обратный, необходимо и достаточно, чтобы
этот оператор действовал взаимно
однозначно из V
в V.
