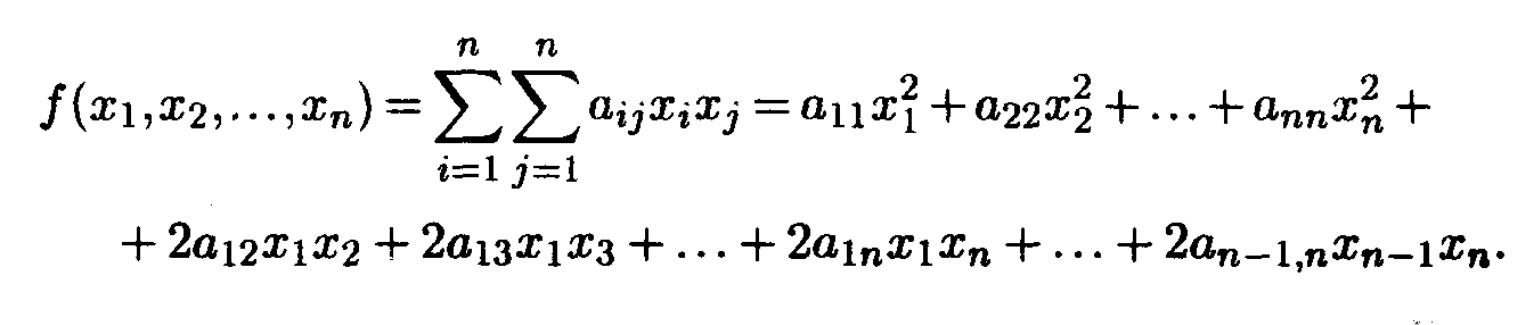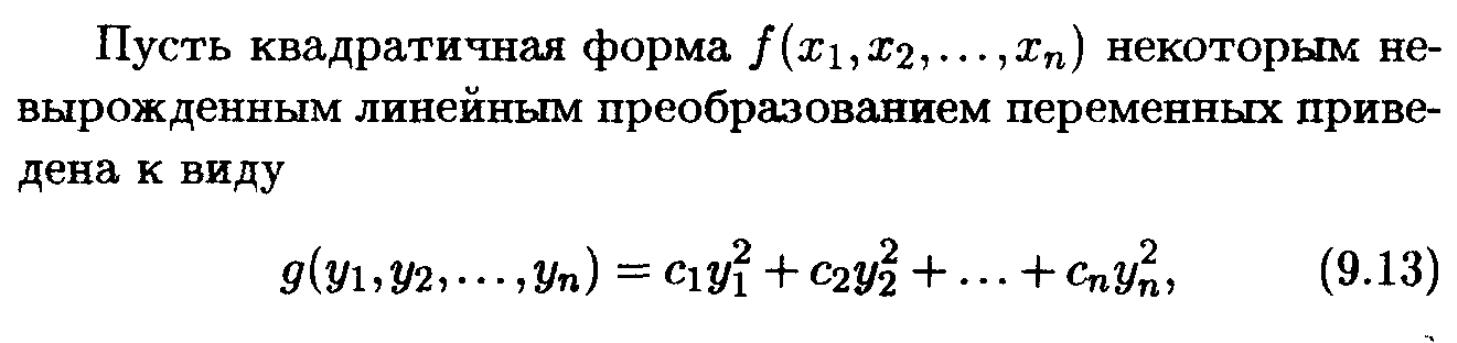- •Пересечение линейных подпространств
- •Скалярное произведение.
- •Для ортонормированных векторов матрица Грама – единичная
- •8. Ортогонализация совокупности векторов.
- •18. Характеристический и минимальный полином. Теоремам Гамильтона-Кели.
- •19. Собственные значения и собственные векторы линейного оператора.
- •Нормальный вид квадратичной формы
18. Характеристический и минимальный полином. Теоремам Гамильтона-Кели.
Многочлен (или полином) от n переменных — это конечная формальная сумма вида
![]() ,
,
где ![]() есть
набор из целых неотрицательных
чисел (называется мультииндекс),
есть
набор из целых неотрицательных
чисел (называется мультииндекс), ![]() —
число (называемое «коэффициент
многочлена»), зависящее только от
мультииндекса I.
—
число (называемое «коэффициент
многочлена»), зависящее только от
мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
![]()
где ![]() фиксированные коэффициенты,
а
фиксированные коэффициенты,
а ![]() —
переменная.
—
переменная.
Характеристический многочлен матрицы — это многочлен, определяющий её собственные значения.
ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН
матрицы ![]() над
полем К
- многочлен
над полем К
над
полем К
- многочлен
над полем К
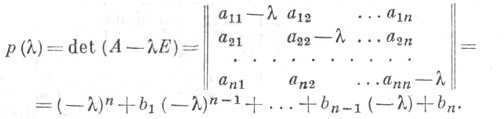
Степень
X. м. равна порядку квадратной
матрицы А, коэффициент
b1 равен следу матрицы .(b1 =
tr A = a11+
а 22+
.. . +а пп),коэффициент b т равен
сумме всех главных миноров
т- гопорядка,
в частности bn=detA. Уравнение ![]() наз.
характеристическим уравнением матрицы А
наз.
характеристическим уравнением матрицы А
Свободный член равен определителю. anƛn+…+ a1ƛ1 +a0=0 – полином n-ой степени.
Некоторый многочлен называется минимальным если он является анулирующим с наименьшей степенью.
Теорема Гамильтона — Кели Любая квадратная матрица удовлетворяет своему характеристическому уравнению.
Если ![]() —
квадратная матрица и
—
квадратная матрица и ![]() её характеристический
многочлен,
то
её характеристический
многочлен,
то ![]() .
.
Разные матрицы могут иметь один и тот же характеристический полином. Коэфиценты называются инварианты.
Матрицы у которых одно и то же характеристическое уравнение эквивалентны.
19. Собственные значения и собственные векторы линейного оператора.
Рассмотрим линейный оператор A, действующий в линейном пространстве X: y = A(x), ∀x ∈ X, y ∈ X.
Число λ называется собственным значением оператора A, если существует такой ненулевой вектор x, что справедливо равенство A(x) = λ·x. Любой ненулевой вектор x ≠0, удовлетворяющий этому уравнению, называется собственным вектором оператора A, отвечающим собственному значению λ.
A(x) = λ·x, x ≠0, x ∈ X.
Число λ = 0 является собственным значением матрицы A:
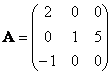
Найдём собственный вектор матрицы, соответствующий собственному значению λ = 0 — то есть найдём нетривиальное решение однородной системы линейных уравнений (A − 0 ·E)·x = 0, x ≠0 :

Действительно, e1 = (0, 5, −1) — собственный вектор, отвечающий собственному значению λ = 0:
20. Жорданова форма матрицы линейного оператора.
Определение.
Жордановой
клеткой
![]() порядка
порядка
![]() называется
матрица порядка
называется
матрица порядка
![]() вида
вида

Жордановой матрицей называется матрица, состоящая из жордановых клеток.
Число клеток равно числу собственных векторов.

У эрмитовой матрицы все жордановы клетки имеют размер 1.
Является матрицей линейного оператора в каноническом базисе.
Жордановы формы двух подобных матриц совпадают с точностью до порядка клеток.
21. Жорданов базис. Присоединенные векторы, жордановы цепочки.
Определение. Пусть λ0 - собственное значение преобразования A и пусть векторы h1,h2,....,hk таковы, что Тогда h1 - собственный вектор преобразования A, а векторы h2,...,hk называют присоединенными векторами к вектору h1. Система векторов h1,...,hk называется жордановой цепочкой для собственного значения λ0, а число k называется длиной жордановой цепочки. Теорема Жордана. Каково бы не было линейное преобразование A в комплексном пространстве , всегда существует базис , составленный из жордановых цепочек для всех собственных значений.
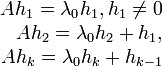
Элемент x называется присоединенным вектором опе-
ратора A, отвечающим собственному значению _, если для некоторого натурального числа
m ≥ 1 выполняются соотношения
(A − _I)m−1x 6= 0, (A − _I)mx = 0.
При этом число m называется высотой присоединенного вектора x. Иными словами, если
x—присоединенный вектор высоты m, то элемент (A − _I)m−1x является собственным
вектором оператора A. Очевидно, собственные векторы—это присоединенные векторы
высоты 1 (здесь (A − _I)0 = I).
Рассмотрим последовательность векторов e1, e2, . . . , em, для которых выполнены соотношения (e1 6= 0):
Ae1 = _e1,
Ae2 = _e2 + e1,
Ae3 = _e3 + e2,
...
Aem = _em + em−1
22. Сопряженные операторы. Матрица сопряженного оператора в произвольном базисе.
Пусть E – конечномерное евклидово пространство.
Определение. Оператор A* :E →E называется сопряженным к
линейному оператору A:E →E , если для любых векторов x, y∈E
выполняется равенство (Ax, y) = (x, A* y).
Утверждение. Оператор A* , сопряженный к линейному оператору A,
является линейным.
Пусть U—Унитарное пространство, A—линейный оператор в U. Оператор A∗ называется сопряженным по отношению к линейному оператору A, если для любых векторов x, y ∈ U выполняется равенство
(Ax, y) = (x,A
∗
y).
Теорема. Сопряженный оператор A∗ обладает следующими свойствами:
1) A∗ —линейный оператор;
2) (A + B)∗ = A∗ + B∗;
3) (αA)∗ = ¯αA∗;
4) (AB)∗ = B∗A∗;
5) (A∗)∗ = A.

23. Самосопряженные операторы. Матрица и ее жорданова форма для самосопряженного оператора.



24. Виды операторов в евклидовых и унитарных пространствах.



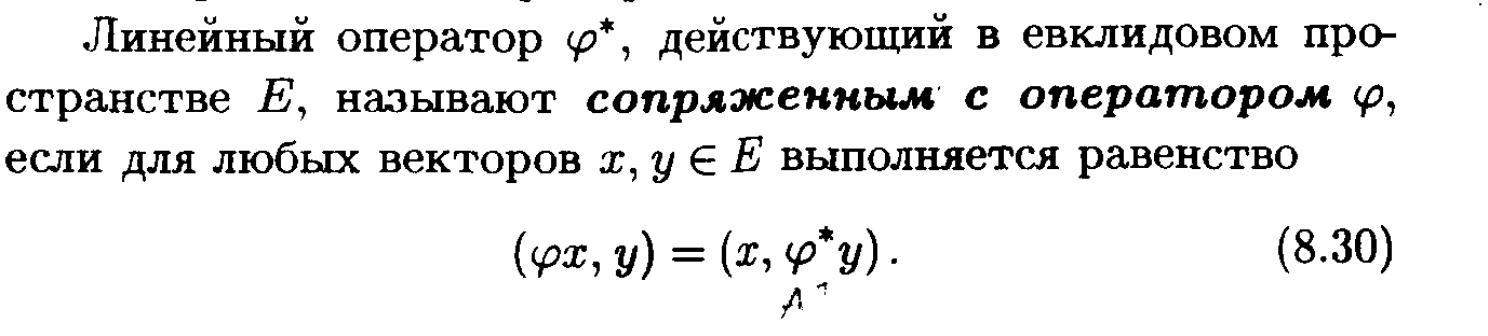





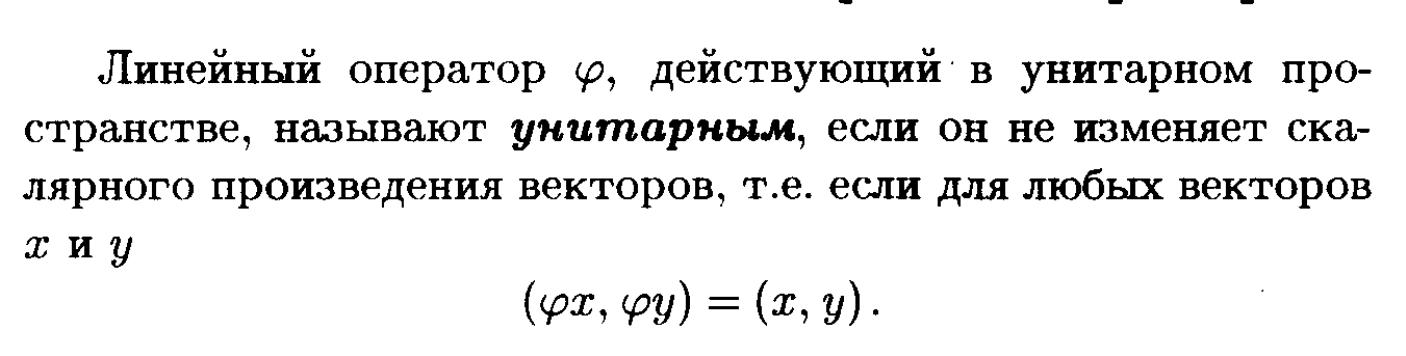

25. Симметричные, ортогональные и нормальные операторы.


Свойства.
![]()
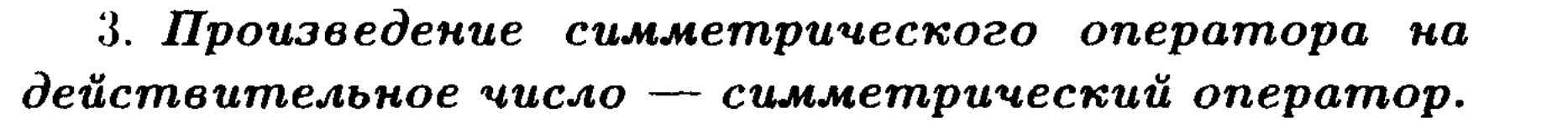
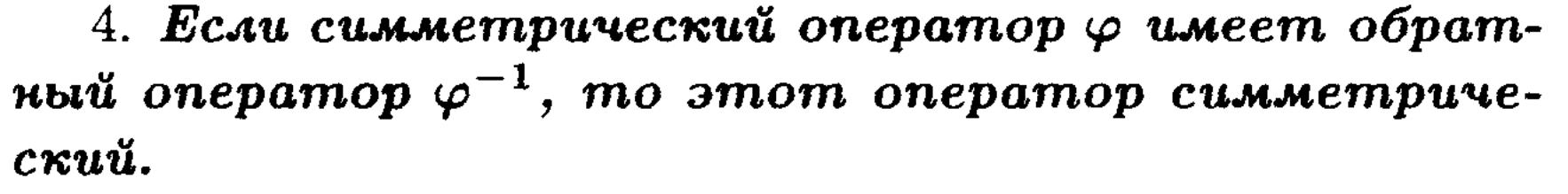
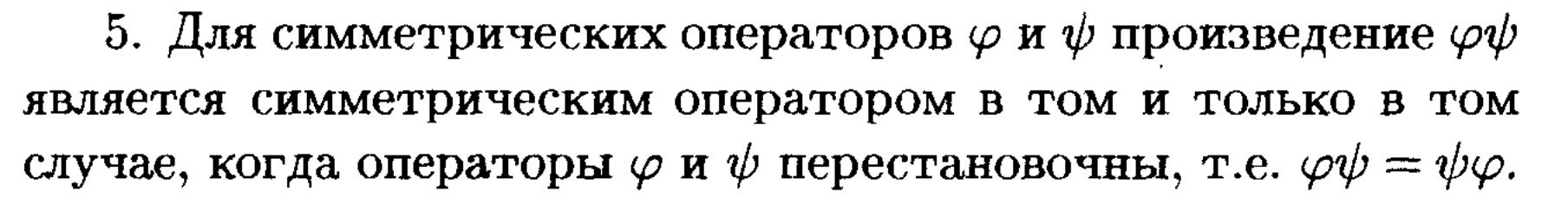


Свойства.




26. Ядро и образ линейного оператора. Свойства.


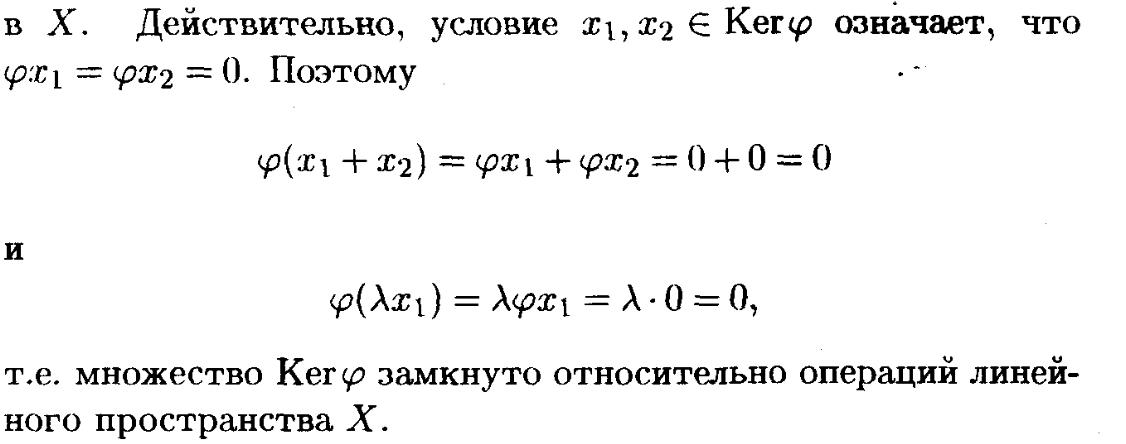

Для линейного оператора, действующего в n-мерном линейном пространстве X, справедливы следующие утверждения:
сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор:
Def(A) + Rg(A) = n;
ранг оператора равен рангу его матрицы;
ядро оператора совпадает с множеством решений линейной однородной системы с матрицей A, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;
столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.
Сформулированные утверждения позволяют описать структуру образа и ядра линейного оператора, заданного матрицей, используя язык матричных преобразований и общей теории линейных систем.
27. Понятие квадратичной формы. Канонический и нормальный вид.