
- •9. Вопросы к экзамену
- •10. Рекомендуемая литература
- •1. Основная литература
- •2. Дополнительная литература
- •Лекция № 2.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция № 3.
- •Основные вопросы, рассматриваемые на лекции:
- •Законы алгебры высказываний
- •Краткое содержание лекционного материала
- •Лекция № 4.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция № 5.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция № 6.
- •Основные вопросы, рассматриваемые на лекции:
- •Лекция № 7.
- •Основные вопросы, рассматриваемые на лекции:
- •Лекция № 8.
- •Основные вопросы, рассматриваемые на лекции:
- •Лекция № 9.
- •Основные вопросы, рассматриваемые на лекции:
- •Непротиворечивость исчисления высказываний
- •Независимость аксиом исчисления высказываний
- •Лекция № 10.
- •Основные вопросы, рассматриваемые на лекции:
- •Лекция №11.
- •Основные вопросы, рассматриваемые на лекции:
- •Операции над предикатами Краткое содержание лекционного материала
- •Лекция №12.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция №13.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция №14.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция №15.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция №15.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция №16.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция №18.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Лекция №19.
- •Основные вопросы, рассматриваемые на лекции:
- •Краткое содержание лекционного материала
- •Практическое занятие №2 Тема: Запись предложений на языке пропозициональной логики
- •Практическое занятие №3 Тема: Тавтологии. Законы логики
- •Практическое занятие №4 Тема: Логическое следование
- •Практическое занятие №5 Тема: Равносильность формул
- •Практическое занятие №6 Тема: Дизъюнктивные и конъюнктивные нормальные формы
- •Практическое занятие №7 Тема: Виды теорем. Необходимые и достаточные условия
- •Практическое занятие №11 Тема: Полные системы связок
- •Практическое занятие №12 Тема: Построение выводов теорем
- •Практическое занятие №13 Тема: Независимость аксиом исчисления высказываний
- •Практическое занятие №14 Тема: Операции над предикатами
- •Практическое занятие №15 Тема: Интерпретации. Виды формул
- •Практическое занятие №16 Тема: Запись математических предложений на языке логики предикатов
- •Практическое занятие №17 Тема: Свойства обобщений и подтверждений
- •Практическое занятие №18 Тема: Логически общезначимые формулы
- •Практическое занятие №19 Тема: Отрицание формул
- •1. Мендельсон э. Введение в математическую логику. – м.: Наука, 1976. – 320 с.
- •2. Игошин в.И. Задачи и упражнения по математической логике и теории алгоритмов. - м.: Академия, 2007. – 304 с.
Лекция №14.
Тема: ОГРАНИЧЕННЫЕ КВАНТОРЫ. ВИДЫ ТЕОРЕМ
Основные вопросы, рассматриваемые на лекции:
Определение ограниченных кванторов
Перенос свойств неограниченных кванторов на ограниченные
Прямая, обратная, противоположная и контрапозитивная теоремы
Краткое содержание лекционного материала
Кванторы вида xD и xD называются также ограниченными.
В математике используются, как правило, ограниченные кванторы (в частности, следующие их видоизменения: xa, xa и т.п.).
Принимаются следующие определения предложений с ограниченными кванторами (ограниченного обобщения и ограниченного подтверждения):
xD P(x)x(xDP(x));
xD P(x)x(xDP(x)).
При таком определении свойства неограниченных кванторов переносятся на ограниченные кванторы: например, свойство отрицания квантора всеобщности:
xD P(x)(определение ограниченного обобщения)
x(xDP(x))(отрицание обобщения)
x(xDP(x))(отрицание импликации)
x(xDP(x))(определение ограниченного подтверждения)
xD P(x).
Теорема, обычно, имеет следующее строение:
xD (P(x)Q(x)), (1)
где P(x), Q(x) – предикаты с областью определения D, или, проще, PQ.
Теоремы вида QP, PQ и QP называются соответственно обратной, противоположной и контрапозитивной к теореме PQ.
Теоремы PQ и QP эквивалентны (по таблице истинности).
Прямая теорема PQ и обратная теорема QP, вообще говоря, не являются эквивалентными. Если прямая и обратная теоремы PQ и QP верны, то их объединяют в одну теорему PQ.
Если импликация PQ истинна (или теорема), то, говорят, что условие Q необходимое для условия P, а условие P достаточное для условия Q. Поэтому теорема PQ формулируется также как теорема о том, что Q является необходимым и достаточным условием для условия P.
Что значит утверждение теоремы (1) не верно?
Ответ следует из свойств отрицания ограниченного обобщения и отрицания импликации: xD (P(x)Q(x)). Чтобы опровергнуть теорему (1), надо найти такое значение a переменной x, что P(a)И и Q(a)Л. Конъюнкция P(a)Q(a) называется контрпримером к теореме (1).
Чтобы доказать теорему вида xD P(x), надо найти такое значение a переменной x, что P(a)И (построении примера к теореме существования).
Лекция №15.
Тема: ЯЗЫКИ ПЕРВОГО ПОРЯДКА И ИНТЕРПРЕТАЦИИ
Основные вопросы, рассматриваемые на лекции:
Логические и нелогические символы языков первого порядка
Термы и формулы языков первого порядка
Интерпретации языков первого порядка
Оценки переменных и значения термов и формул
Свободные и связанные вхождения переменных
Краткое содержание лекционного материала
Каждый язык первого порядка L определяется одним и тем же множеством логических символов и одними и теми же правилами построения термов и формул. Отличаются языки первого порядка множествами нелогических символов.
Логические символы: переменные, логические связки, кванторы. Переменных имеется счетное множество. Логические связки и кванторы подразделяются на два вида: неопределяемые и определяемые. Мы в качестве неопределяемых символов рассмотрим логические связки , и квантор .
Нелогические символы: константы, n-арные функциональные и предикатные символы (n1). Множество нелогических символов содержит хотя бы один предикатный символ.
Термами и формулами языка L называются слова в алфавите языка L, которые получаются строго по следующим правилам:
1) переменная – терм;
2) константа – терм;
3) слово вида ft1...tn – терм, если f – n-арный функциональный символ, а t1, ..., tn – термы;
4) слово вида Pt1...tn – формула, если P – n-арный предикатный символ, а t1, ..., tn – термы;
5) слово вида A – формула, если A – формула;
6) слово вида AB – формула, если A и B – формулы;
7) слово вида xA – формула, если x – переменная, а A – формула.
Пусть L – язык первого порядка (с равенством или без равенства).
Интерпретация нелогических символов I языка L – это непустое множество I, на котором определены следующие объекты:
элемент eI для каждой константы e из L;
n-местное отображение fI:InI для каждого n-арного функционального символа f из L;
n-местное отношение PIIn для каждого n-арного предикатного символа P из L (кроме ).
Оценка (иначе интерпретация) v переменных языка L – это некоторое отображение v множества X всех переменных языка L в множество I.
Пара (I,v), состоящая из некоторой интерпретации I нелогических символов языка L и некоторой оценки v переменных языка L называется интерпретацией I при оценке v. Обозначение: Iv.
Через vx обозначим любую оценку следующего вида:
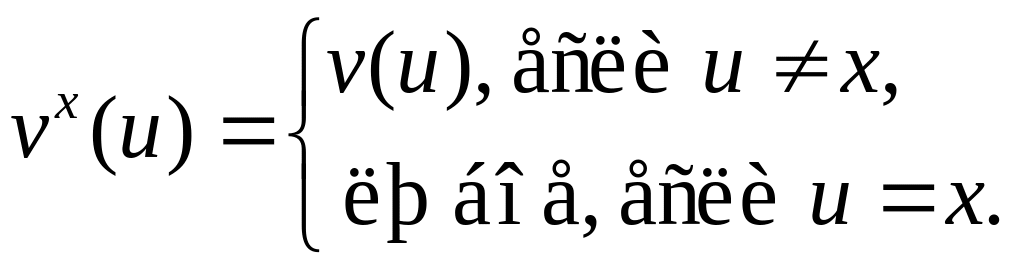
Определим по индукции значение Iv(t) терма t и истинностное значение Iv(A) формулы A языка L в интерпретации I при оценке v:
Iv(x)v(x) для переменной x из L;
Iv(e)eI для константы e из L;
Iv(ft1…tn)fI((t1)I,…,(tn)I) для терма ft1…tn из L;
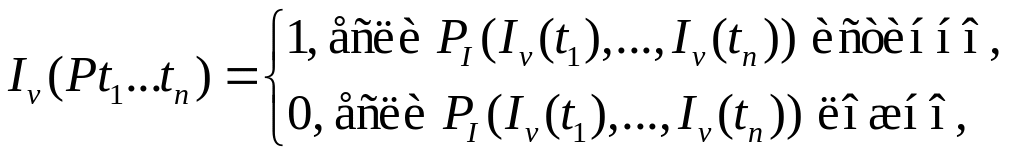
для предиката Pt1…tn из L (кроме );
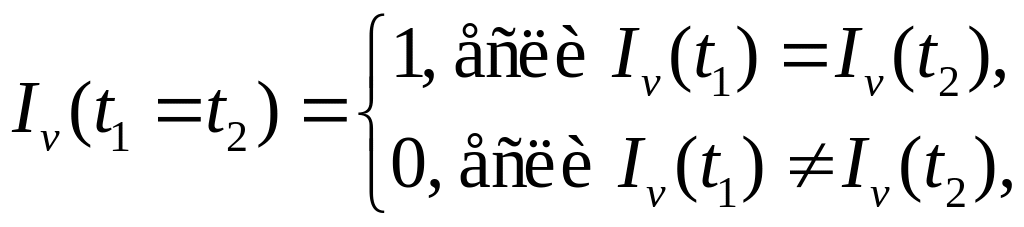 для
равенства t1t2
из L;
для
равенства t1t2
из L;
 для
отрицания B
из L;
для
отрицания B
из L;
 для
импликации BC
из L;
для
импликации BC
из L;
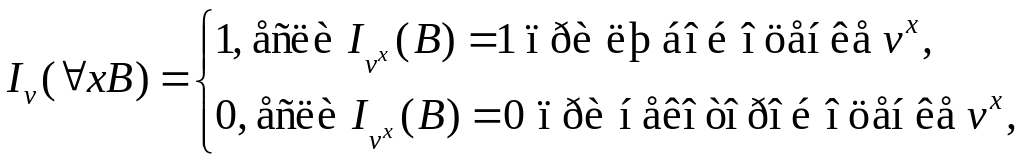 для
обобщения xB
из L.
для
обобщения xB
из L.
Формула A языка L называется в интерпретации I:
истинной, если Iv(A)1 при любой оценке v;
выполнимой, если Iv(A)1 при некоторой оценке v;
опровержимой, если Iv(A)0 при некоторой оценке v;
ложной, если Iv(A)0 при любой оценке v.
Истинные (ложные) формулы в интерпретации I называются иногда тождественно истинными (тождественно ложными) на множестве I.
Отметим, что формулы, истинные (ложные) и неопровержимые (невыполнимые) в интерпретации I, совпадают.
В каждой интерпретации I формулы подразделяются на 3 вида: истинные, выполнимые и опровержимые, ложные. Пример: в одноэлементной интерпретации формула xy истинна и формула xy ложна, а в интерпретации с более чем одним элементом обе эти формулы выполнимы и опровержимы.
Формула A языка L называется:
истинной, если A истинна в каждой интерпретации I;
выполнимой, если A истинна в некоторой интерпретации I;
опровержимой, если A ложна в некоторой интерпретации I;
ложной, если A ложна в каждой интерпретации I.
Истинные (ложные) формулы также называются логически общезначимыми формулами (противоречиями).
Формулы подразделяются на 3 вида: логически общезначимые, выполнимые и опровержимые, противоречия. Пример: формула xx истинна, формула xx ложна, а формулы xy и xy и выполнимы, и опровержимы.
Пример. Пусть P – бинарный предикатный символ. Тогда:
1) формула P(x,y)P(x,y) логически общезначима по определению связки ;
2) формула xyP(x,y)yxP(x,y) логически общезначима по смыслу квантора ;
3) формула P(x,y)P(x,y) выполнима, так как предложение xyxy истинно на одноэлементном множестве;
4) формула P(x,y)P(x,y) логически не общезначима, так как предложение xyxy не истинно на двухэлементном множестве;
5) формула (P(x,y)P(x,y))) является противоречием определению связок и .
Предложение формальной или естественной теории называется логически истинным (логически ложным), если является частным случаем логически общезначимой (невыполнимой) формулы языка первого порядка.
Формулы A и B языка L называются логически эквивалентными, если AIBI для любой интерпретации I языка L и для любых значений переменных. Формулы A и B языка L логически эквивалентны тогда и только тогда, когда формула AB логически общезначима.
Формулы A языка L логически следует из множества формул языка L, если для любой интерпретации I языка L и для любых значений переменных AI1 каждый раз, когда BI1 для всех B. При этом Формула A называется логическим следствием формулы B.
Подформула B формулы A – это часть формулы A, также являющейся формулой. Вхождение переменной x в формуле A связанное (свободное), если это вхождение (не) является частью подформулы формулы A вида xB.
Запись Ax[t] обозначает формулу, которая получается из формулы A заменой каждого вхождения переменной x термом t; при этом предполагается, что терм t допустим для подстановки в формулу A вместо переменной x, т.е. формула A не содержит подформул вида yB, где y – переменная из t.
Приведем пример, показывающий необходимость ограничения допустимости термов для подстановки вместо переменных. Пусть P – унарный предикатный символ, формула A имеет вид y(P(x)P(y)), терм t является переменной y. Тогда формула Ax[t] имеет вид y yy, и получается, что формула A выполнима, но формула Ax[t] невыполнима.
