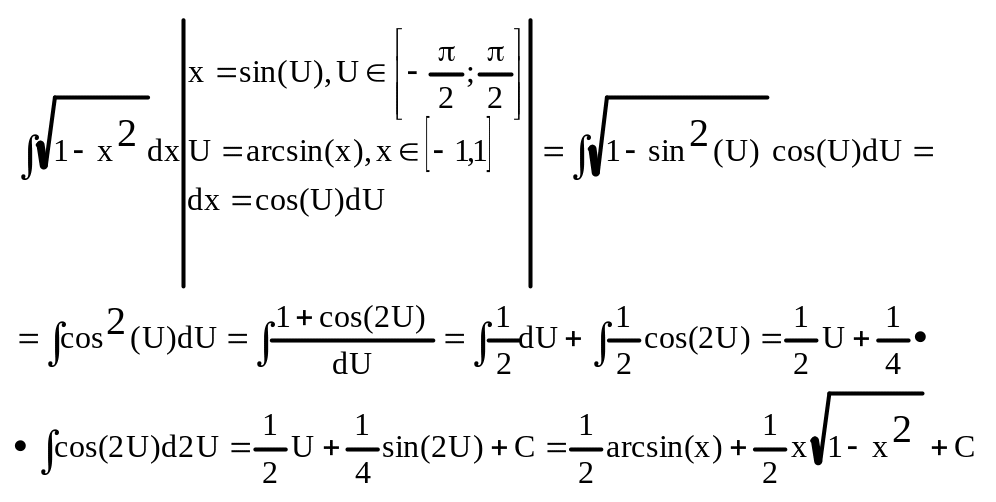Определения и свойства неопределенного интеграла первообразная Н.И.

Опр.1. пусть функция f(x) на некотором конечном или бесконечном промежутке I числовой оси R, т.е. на интервале полуинтервале или отрезке. Функция F(x) определена на этом же промежутке и называется первообразной функции f(x) на I, если:

1. Функция F(x)непрерывна на I;

2. во всех внутренних точках промежутка I, функция F(x) имеет производную и, что .

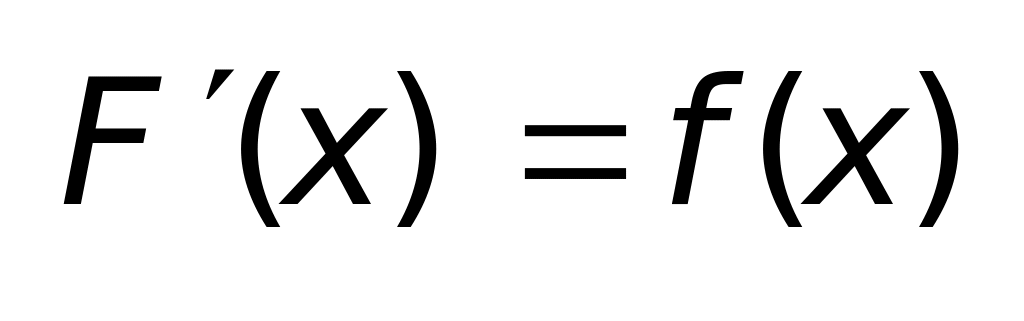Определение 1 Функция F(x) называется первообразной на интервале (a,b) для функции f(x), если в любой т. x, интервала (a,b) функция F(x) дифференцируема и имеет производную равную: F’(x) = f(x).

Имеет место теорема:

Если функция F(x) является какой либо первообразной для функции f(x) на промежутке I, тогда любая функция Ф(x) вида:

Ф(x) = F(x) + C, xI,

также является первообразной функции f(x) и всякая первообразная функции представлена в виде:

F(x) + C;

Док – во:

Если F(x) первообр. функции f(x) на I, то для любых C – const функция F(x)+C также непрерывна на I, как сумма непрерывных функций. И производная:

(F(x)+C)’=P’(x)+C’=F’(x)=f(x),

т.е. функция F(x) + C является первообразной, функции f(x) на I.

С другой стороны в силу следствия критерия постоянства функции f(x) на I, если F(x) и Ф(x) две первообразные для функции f(x) на I, т.е. F(x) и Ф(x) непрерывны на I и дифференцируемы внутри I, и, кроме того:

F’(x) = f(x) и Ф(x) = f(x), то F(x) - Ф(x) = С, а тогда Ф(x) = F(x) + С;

Определение 2 Совокупность всех первообразных функции f(X) определена на некотором промежутке I, называется неопределенным интегралом (н.И.) от функции f(X) на этом промежутке и обозначается: .

Основные свойства Н.И.

1. Пусть функция F(x) непрерывна на I и дифференцируема в его внутренних точках, тогда интеграл равен:

или

Доказательства следуют из равенства (4) и определения Н.И. (3).

2. Пусть функция имеет первообразную на промежутке I, тогда для любой внутренней точки промежутка I, имеет место равенство:

Док – во:

3. Если f₁(x) и f₂(x) имеют первообразную на I то и функция равная сумме этих функций имеет первообразную на этом же промежутке, причем интеграл от суммы этих функций будут равняться сумме И.

Св-во адетивности интеграла функции:

Док-во:

Пусть: и

Следовательно функции F₁(x) и F₂(x) непрерывны на I во всех его внутренних точках этого промежутка справедливо равенство:

F₁’(x)=f₁(x); F₂’(x)=f₂(x);

Положим F(x)=F₁(x)+F₂(x),тогда F(x) непрерывна на I, как сумма непрерывных функций, и во внутренней точке этого промежутка.

F’(x)=(F₁(x)+F₂(x))’=F₁’(x)+F₂’(x)=f₁(x)+f₂(x), т.е.

F(x) является первообразной для f₁(x)+f₂(x) на инт. I. И поэтому:

таким образом, имеем:

В силу произвольности С₁, С₂, С эти совокупности совпадают и имеют место равенство:

;

4. Если f(x) имеет первообразную на I и k некоторое число, то функция k*f(x), также имеет на I, первообразную, причем при k0 имеет место равенство:

;

все необходимые свойства неопределенного интеграла.

3.Табличные интегралы

Операция нахождения Н. И. От данной функции называется интегрированием и является операцией обратной дифференцированию.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

4.Замена переменных (введение множителя под знак дифференциала)

Теорема1: Пусть функция  определена и непрерывна на промежутке , дифференцируема внутри его и отлична от постоянной. Функция g определена на промежутке I =() и имеет на этом промежутке первообразную G. Пусть, кроме того f(x)=g((x)) ’(x). Тогда, кроме того, f(x) имеет первообразную на :

Док-во: т.к. функция  непрерывна на , то в силу следствия т. Больцмана- Каши , I=(x) это есть промежуток, при чем т.к.  не является const, то I не обращается в точку.

Поскольку G является первообразной g на I, то она непрерывна на I и дифференцирована во всех внутренних т. т.к.  по условию теоремы непрерывна на , то имеет смысл сложная функция:

F(x)=G((x))

Определенная на  и непрерывная:

F’(x)=G’((x)) ’(x)=g((x)) ’(x)=f(x)

Следовательно F(x) является первообразной для f(x) и тогда:

Теорема2: Пусть функция  непрерывна на промежутке I, строго монотонна на нем и дифференцируема в каждой внутренней т. I.

Если функция g(U)=((U)) ’(U) имеет первообразную на I, то функция f имеет первообразную на промежутке =(I):

(x) – это функция по  обратная к .

Док – во

В силу условия теоремы на промежутке  определена, непрерывна и дифференцируема во всех внутренних точках, обратная к  функция (x).

Пусть G первообразная на промежутке I для g(U) и пусть F равное:

F=G((x))

Тогда F непрерывна на  как композиция непрерывных функций и дифференцируема во внутр. т. .

F’(x)= G’((x)) ’(x)=g((x)) ’(x)=f(((x))) ’((x)) ’(x)=f(x)

Таким образом F(x) определяемая F=G( (x)) это первообразная функции на . А, следовательно:

Пример:

1.

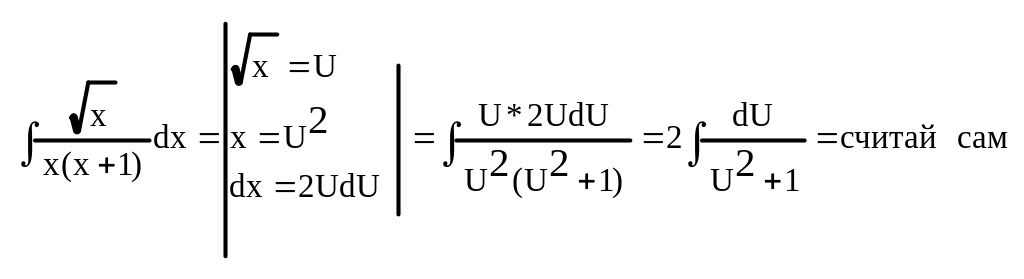
2.