8. Приведите пример анализа линейных электрических цепей методом узловых напряжений.

Пусть анализу подлежит схема рис. 2.8, а. Схема содержит активные и пассивные ветви, соединенные параллельно. Определим токи всех ветвей цепи.

Обозначим сложные потенциальные узлы схемы индексами А и В. Напряжение U^I_АВ между узлами А и В, создаваемое только источником тока I, определим по схеме рис. 2.8, б. Согласно первому закону Кирхгофа, ток источника I равен сумме токов всех ветвей: Отсюда

где:g_i – проводимость i-ой ветви (кроме ветви с источником тока).

напряжение и , создаваемое источником Э.Д.С. Е_1, можно определить по:

Результирующее напряжение U_АВ, определим как сумму от воздейст-вия источников I, Е₁ и Е₂. Значения знаменателей в выражениях (2.13), (2.14), (2.15) одинаковы. Поэтому

т. е. (2.16)

В выражении (2.16) произведения g_i,∙E_i и I_i берут со знаком плюс, когда направления Е_i и I_i противоположны выбранному условно – положи тельному направлению напряжения U_АВ, и со знаком минус, когда эти

направления совпадают.

Зная междуузловое напряжение U_АВ, легко найти токи, как в пассивных, так и в активных ветвях цепи рис. 2.8, а:

9. Раскройте суть анализа линейных электрических цепей методом эквивалентного активного двухполюсника.

Обоснованием данного метода является теорема об активном эквивалентном двухполюснике. Теорема утверждает, что любую, сколь угодно сложную электрическую цепь или ее часть, можно представить активным эквивалентным двухполюсником с параметрами Е_экв и R_экв. Режим работы ветви, присоединенной к двухполюснику, при этом не изменится.

Пусть анализу подлежит схема электрической цепи, приведенной на рис. 2.9, а. Предположим, что в этой цепи нас интересуют напряжение и ток только одной ветви – R₃. всю схему, кроме ветви R₃, представим активным двухполюсником (рис. 2.9, б). К зажимам двухполюсника а и б присоединим ветвь R₃.

Параметры двухполюсника R_экв и Е_экв определяются составом и топологией схемы цепи рис. 2.9, а. Поэтому режим работы ветви R₃ не изменился. Но теперь для определения тока в ней достаточно применить закон Ома:

(2.17)

В этом и заключается преимущество рассматриваемого метода.

Для решения (2.17) необходимо определить значения Е_экв и R_экв. Значение Е_экв определяют исходя из того, что напряжение U_хх на разомкнутых зажимах источника равно значению его Э.Д.С. – Е_экв.

Таким образом, метод активного эквивалентного двухполюсника существенно упрощает процесс анализа, но требует определенных навыков в преобразовании топологии схемы к удобному и наглядному виду.

10. Сформулируйте определения, приведите основные параметры синусоидального тока (напряжения).

Переменным называют ток (напряжение, Э.Д.С.), изменяющийся во времени по величине и направлению. Синусоидальный ток может быть представлен посредством действительной функции времени – синусной или косинусной, например,

, (3.1)

где I_m – максимальная амплитуда тока (амплитудное значение);

 – угловая частота, причем ; f – частота колебаний [Гц]; Т – период [C]; _i – начальная фаза, определяет значение тока в момент времени t=0, т.е.

i(t=0) = I_m sin _i.

На рис. 3.1 приведен график двух колебаний с разными начальными

фазами _{1 и} ₂, причем ₁ < ₂. Амплитуда гармоник проходит через нуль, когда

t +  = n, (n = 0,1,2...),

т.е. в моменты .

Так как ₁< ₂, то t₂ имеет место раньше t₁.

Рис. 3.1. Графики мгновенных значений синусоидального тока i₁(t) = I_m∙sin ωt

и I₂(t) = I_m∙sin(ωt+30º)

Начальная фаза часто задается в градусах. Поэтому при определении мгновенного значения тока аргумент синуса (слагаемые t и ) нужно привести к одной единице измерения (радиан или градус).

Иногда гармоническое колебание представляется в косинусной форме. Легко видеть, что для перехода к такой форме в (3.1) достаточно изменить лишь начальную фазу, т.е.

Выражение для синусоидального напряжения аналогично, т.е. u(t) = U_m  sin (t + _u).

Под средним значением синусоидального тока понимают его среднее значение за половину периода: .

Действующим называют среднее квадратичное значение синусоидального тока (напряжения) за период . .

Если говорят о значениях переменного тока или напряжения, то, как правило, подразумевают их действующие значения. Например, напряжение в однофазной сети переменного тока 220 В - действующее. При этом амплитудное значение U_m  310 В.

11. Проведите переход от представления тока в форме действительной функции синуса к представлению в форме радиус – вектора. Для каких цепей применяют представление в форме радиус – вектора. При анализе состояния электрических цепей переменного тока возникает необходимость вычисления суммы или разности колебаний одинаковых

частот, но с разными амплитудами и разными начальными фазами. Решать такую задачу с помощью рассмотренной формы представления (т.е. с помощью тригонометрических функций) достаточно трудно.

Пусть нужно найти ток i(t) = i₁(t) + i₂(t), причем:

i₁(t) = I_m1 sin ( t + ₁),

i₂(t) = I_m2 sin ( t + ₂).

Так как частоты колебаний одинаковы, то задача сводится к нахождению суммарных амплитудного значения тока I_m и начальной фазы . Если применить для решения известные тригонометрические преобразования, то получим:

, .

Видим, что даже окончательный результат имеет громоздкий и не наглядный вид.

Значительное упрощение достигается применением графического метода. Векторное представление синусоидальных величин известно из тригонометрии. Синусоидальный ток (напряжение) изображается в виде радиус-вектора, вращающегося против часовой стрелки с частотой . Длина вектора равна амплитудному значению - I_m. Один оборот вектор совершает за время одного периода (рис.3.2).

Положение радиус-вектора относительно оси Х в момент начала отсчета t=0 определяется углом . Проекция вектора на ось Y определяется выражением (3.1).

На одной векторной диаграмме могут быть изображены векторы нескольких колебаний, например, i₁(t) и i₂(t) (рис. 3.3). Для упрощения анализа все векторы изображаются в момент времени t=0. Тогда сумма двух векторов определится по правилу параллелограмма.

Результирующий радиус-вектор также вращается относительно начала координат с частотой , а его проекция на ось Y определяется выражением i(t) = I_m  sin ( t + ),

где  - положение суммарного вектора относительно оси Х в момент времени t=0.

Простота решения очевидна. Однако графический метод обладает существенным недостатком – низкой точностью. Поэтому его применяют чаще всего для качественного анализа электрических цепей с помощью топографических векторных диаграмм напряжений.

12. Когда применяют комплексное изображение синусоидального тока (напряжения)? Покажите связь между алгебраической и показательной формами комплексного представления. Комплексное представление синусоидальных токов и напряжений позволяет совместить простоту и наглядность векторного представления с точностью представления действительными функциями времени.

где j – мнимая единица, причем –

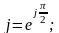Выражение определяет комплексную алгебраическую форму представления синусоидального тока. Она удобна для выполнения действий сложения и вычитания токов (напряжений). Действительно, для сложения двух комплексных чисел достаточно отдельно сложить их действительные и мнимые части.

Подставим в (3.5) вместо и их значения. Тогда получим:

, (3.6)

где – модуль комплексного представления тока, численно равный амплитудному значению.

Выражение (3.6) определяет комплексную тригонометрическую форму представления синусоидального тока.

, а .

Видим, что выражения характеризуют параметры синусоидального тока, не зависящие от времени - действительную амплитуду и начальную фазу . Они позволяют легко перейти от комплексной формы представления к представлению действительными функциями времени.

Введем зависимость от времени. Тогда ,

где

С помощью формулы Эйлера от (3.6) переходят к показательной форме комплексного представления тока: .

С учетом зависимости от времени выражение принимает вид:

_.

Показательная комплексная форма удобна для выполнения действий умножения, деления, возведения в степень или извлечения корня. Действительно, для умножения двух комплексных чисел в показательной форме достаточно перемножить их модули, а аргументы (показатели степени) сложить.

Для элемента с резистивным сопротивлением справедливо равенство:

Векторы тока и напряжения будут совпадать

Для элемента, обладающего емкостью, известно выражение:

Таким образом видим, что напряжение на емкости отстает от тока на 90^о

Для элемента, обладающего индуктивностью .

Видим, что напряжение на индуктивности опережает ток на 90^о