Пп 10. Функции. Непрерывность основные определения и формулы Числовые множества

– множество натуральных чисел ;

– множество целых чисел ;

– множество рациональных чисел вида ;

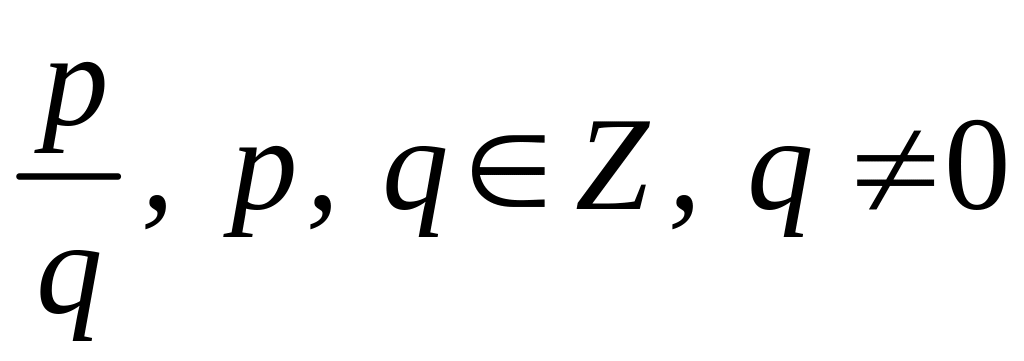– множество иррациональных чисел .

– Множество действительных (вещественных) чисел, .

носится к установлению соответствия между элементами двух множеств.

Если задано правило , по которому каждому элементу из множества поставлен в соответствие единственный элемент из множества , то говорят, что на множестве задана функция , , . Множество называется областью определения функции (ООФ) и обозначается . Множество изменения функции называется областью значений функции (ОЗФ) и обозначается .

При нахождении области определения следует помнить, что:

; ; ;

; .

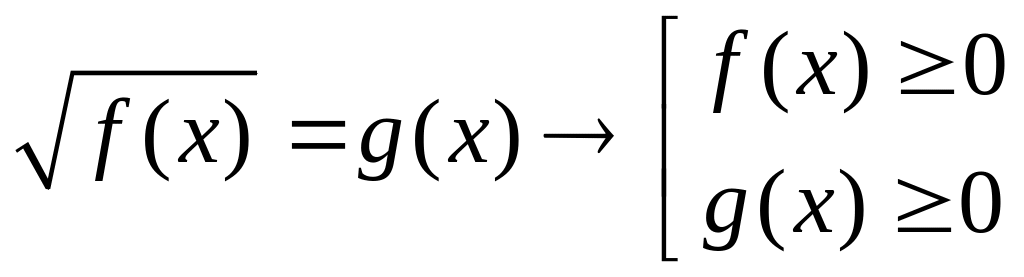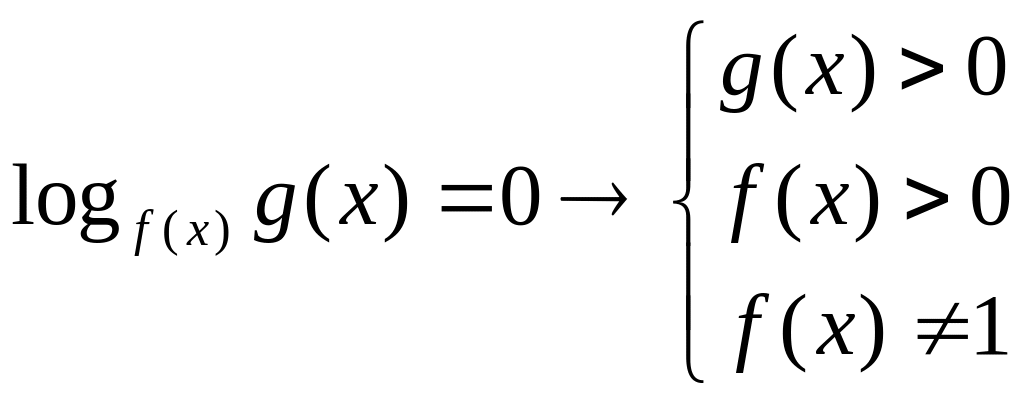При аналитическом задании функция может быть определена:

1) явно - уравнением вида ;

2) неявно - уравнением вида ; Уравнение может определять не одну, а несколько функций вида . Так, уравнение определяет две функции: и .

3) параметрически – .

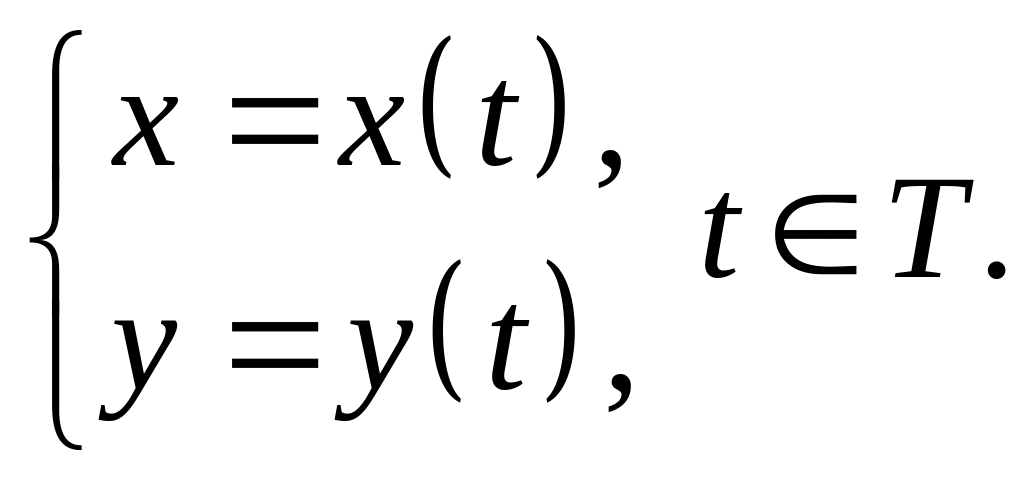Функция с симметричной относительно нуля областью определения называется четной, если для любого выполняется равенство .

Из определения четной функции следует, что ее график симметричен относительно оси ординат. Например, функции , являются четными, их графики имеют вид:

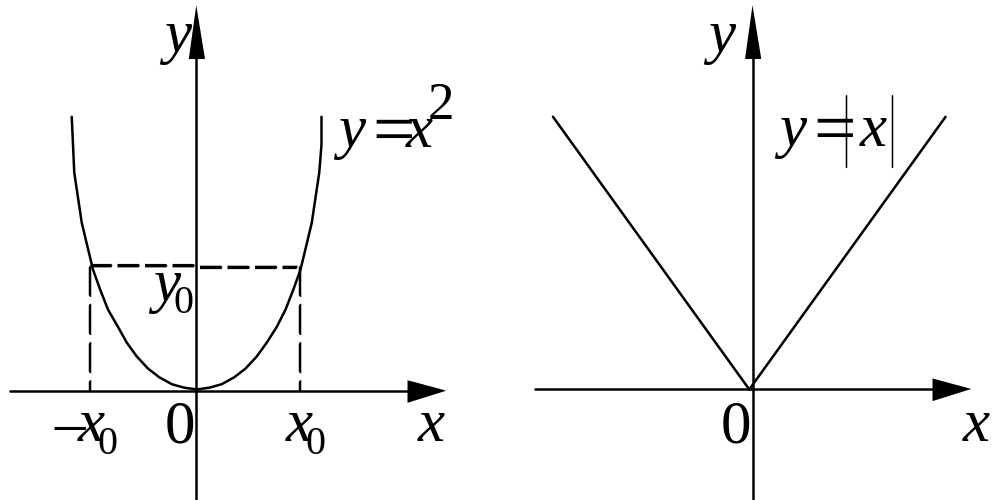
Функция с областью определения называется нечетной, если для любого выполняется равенство .

График нечетной функции симметричен относительно начала координат. Например, функции и являются нечетными, их графики имеют вид:

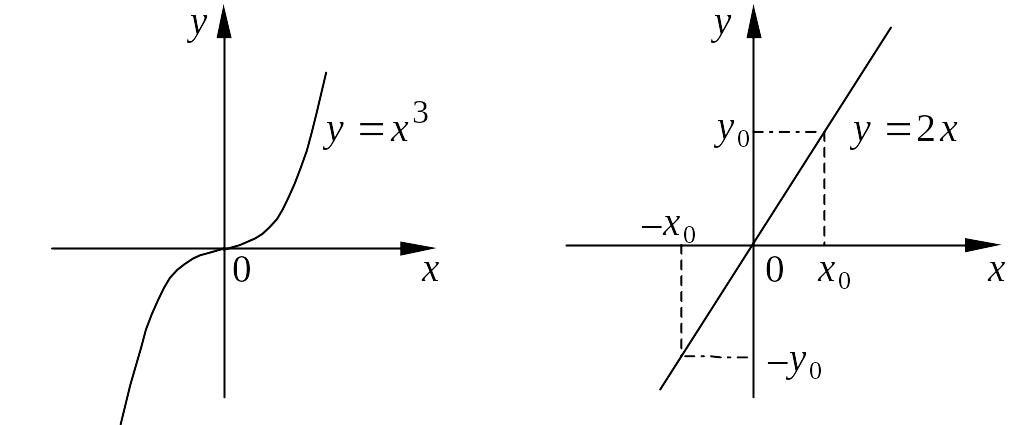
Функция не является ни четной, ни нечетной, так как .

Функция называется периодической, если существует такое число , что для любого выполнены условия: 1) ; 2) .

Число называется периодом функции .

Если – период, то тоже является периодом:

,

а также

, , .

Наименьший положительный период называется основным периодом данной периодической функции.

Основной период функций , равен , а функций , равен . Период функций и равен . Функция основного периода не имеет, так как при любом , в том числе и при .

Функция называется ограниченной на множестве , если

.

Например, функция ограничена на всей числовой оси; ограничена на любом промежутке конечной длины, но не ограничена на всей области определения .

Функция называется ограниченной сверху (снизу) на множестве , если ; ( ).

Например, ограничена снизу на всей области определения .

Точная верхняя (нижняя) грань множества значений функции на называется точной верхней (нижней) гранью функции на и обозначается ( ).

Например, , .

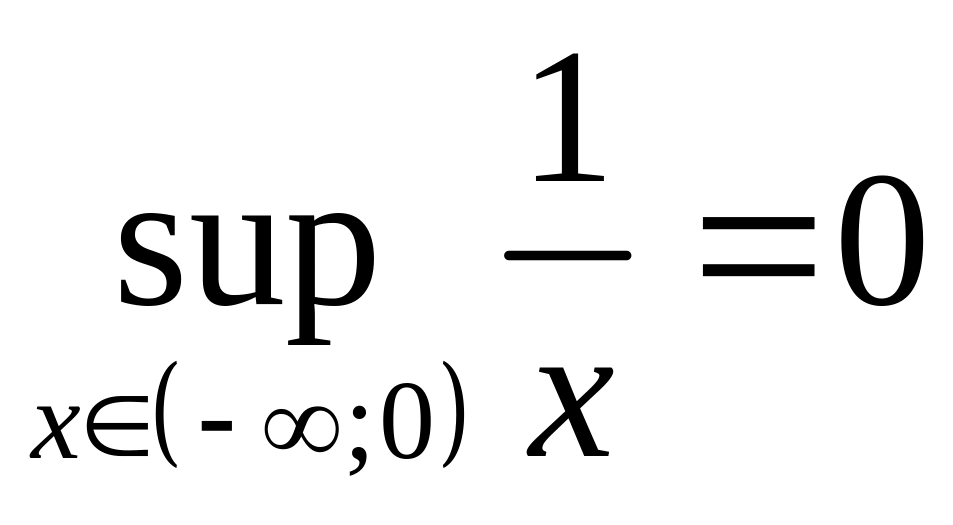Если число ( ) принадлежит множеству значений функции на , то оно называется наибольшим (наименьшим) значением на и обозначается ( ).

Например, , не существует.

Пусть определена на множестве и множество .

Если :

- возрастающая на ;

- неубывающая на ;

- убывающая на ;

- невозрастающая на .

Все четыре типа в совокупности называются монотонными на , а возрастающие и убывающие - строго монотонными на .

Обратная функция. Сложная функция

Функция , , обратима, если каждое свое значение она принимает один раз, то есть для каждого существует только одно значение такое, что .

Для нахождения обратной функции нужно:

1. выразить через ;

2. поменять местами и .

Множество значений обратной функции совпадает с областью определения функции , а область определения обратной функции совпадает с множеством значений функции .

Графики функций и симметричны относительно биссектрисы первого и третьего координатных углов, то есть прямой .

Если и - функции одного переменного, то функция , определенная соотношением на области , называется сложной функцией или суперпозицией (композицией) функций и и обозначается .

Основные элементарные функции