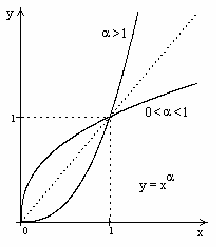
1. Степенные функции
1.1.
|
||
|
|
|
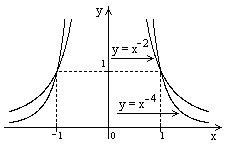
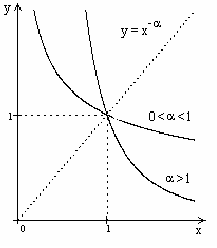
1.2.
|
||
|
|
|
1.3.
|
||
|
|
|
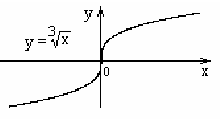
1.4.
|
||
|
|
|
2. Трансцендентные функции
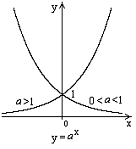
2.1. Показательная
|
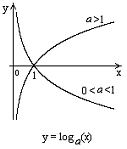
2.2.
Логарифмическая
|
|
|
3. Тригонометрические функции
|
|
3.1.
|
3.2.
|
|
|
3.3.
|
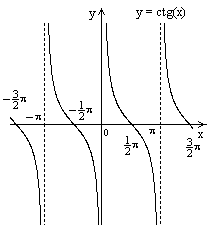
3.4.
|
|
|
.
4. Обратные тригонометрические функции
|
|
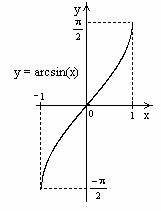
4.1.
|
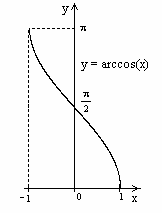
4.2.
|
|
|
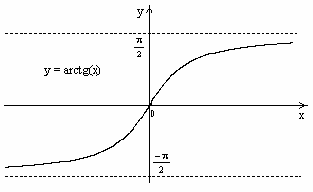
4.3.
|
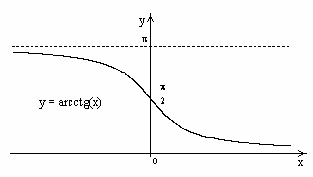
4.4.
|
|
|
|
|
5. Гиперболические функции
|
|
5.1. Гиперболический синус
|
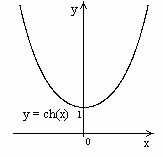
5.2. Гиперболический косинус
|
|
|
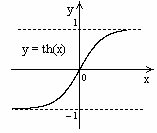
5.3. Гиперболический тангенс
|
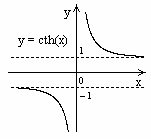
5.4. Гиперболический котангенс
|
|
|
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Непрерывность функции
Определение 1.
Пусть
функция
![]() определена на множестве
определена на множестве
![]() и пусть точка
и пусть точка
![]() .
Функция
называется непрерывной
в точке
.
Функция
называется непрерывной
в точке
![]() ,
если 1)
,
если 1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() .
.
Функция
называется непрерывной
в точке
,если
по любому
![]() можно указать такое
можно указать такое
![]() ,
что
,
что![]() ,если
,если
![]() .
.
Определение 2.
Функция
называется непрерывной
в точке
,
если функция определена в точке
и при этом
![]() ,
то есть бесконечно малым приращениям
аргумента соответствуют бесконечно
малые приращения функции.
,
то есть бесконечно малым приращениям
аргумента соответствуют бесконечно
малые приращения функции.
Определение 3.
Функция
называется непрерывной
в точке
,
если функция определена в точке
,
существуют односторонние пределы
![]() и при этом
и при этом
![]() .
.
Функция
называется непрерывной
в точке
слева, если
функция определена в точке
и существует
односторонний предел
![]() и при этом
и при этом
![]() .
.
Функция
называется непрерывной
в точке
справа, если
функция определена в точке
и существует
односторонний предел
![]() и при этом
и при этом
![]() .
.
Функция, непрерывная в любой точке множества , называется непрерывной на множестве .
Свойства непрерывных функций
Если
функции
и
![]() определены на множестве
и непрерывны в точке
,
то функции
определены на множестве
и непрерывны в точке
,
то функции
![]() ,
,
![]() ,
,
![]() ,
,
![]()
непрерывны
в точке
![]() ,
причем частное требует условия
,
причем частное требует условия
![]() .
.
Если![]() непрерывна на
непрерывна на
![]() ,
то она ограничена на этом отрезке
(
,
то она ограничена на этом отрезке
(![]() и
и
![]() :
:
![]()
![]() ).
).
Если непрерывна на , то она достигает на нем своих точной верхней и точной нижней граней
(![]() ).
).
О
прохождении непрерывной функции через
ноль. Если
функция y
=
непрерывна на
и имеет на концах отрезка значения
![]() и
и
![]() разных
знаков, то найдется точка
разных
знаков, то найдется точка
![]() такая,
что
такая,
что![]() .
.
О
прохождении непрерывной функции через
любое промежуточное значение.
Если функция
y=
-
непрерывна на
,
имеет на концах отрезка значения
![]() и число С
расположено между числами А
и В
:
и число С
расположено между числами А
и В
:
![]() ,
то найдется точка
,
то найдется точка
![]() такая, что
такая, что
![]() .
.
Теорема
применяется для отыскания корней
уравнения вида
![]() методом половинного деления отрезка.
методом половинного деления отрезка.
Непрерывность обратной функции
Если:
1)
![]() - строго монотонная, непрерывная на
,
- строго монотонная, непрерывная на
,
2)
![]() ,
то
,
то
![]() - строго монотонная, непрерывная на
- строго монотонная, непрерывная на
![]() .
.
1).
Если исходные
функции непрерывны, то в результате их
сложения, вычитания, умножения, деления
(если знаменатель
![]() ),
взятия обратной и сложной функций
получаются непрерывные функции.
),
взятия обратной и сложной функций
получаются непрерывные функции.
2).
Для непрерывной
в точке
![]() функции
функции
![]() справедливо:
справедливо:
![]() .
.
Для непрерывных функций переходить к пределу можно под знаком функций:
а)
![]() ,
,
б)
![]() .
.
Классификация точек разрыва
Если
односторонние пределы существуют,
причем
![]() а функция y
= f(x)
не определена в точке x0,
или
а функция y
= f(x)
не определена в точке x0,
или
![]() то точка x0
называется точкой
устранимого разрыва.
то точка x0
называется точкой
устранимого разрыва.
Устранимый разрыв можно устранить, вводя функцию
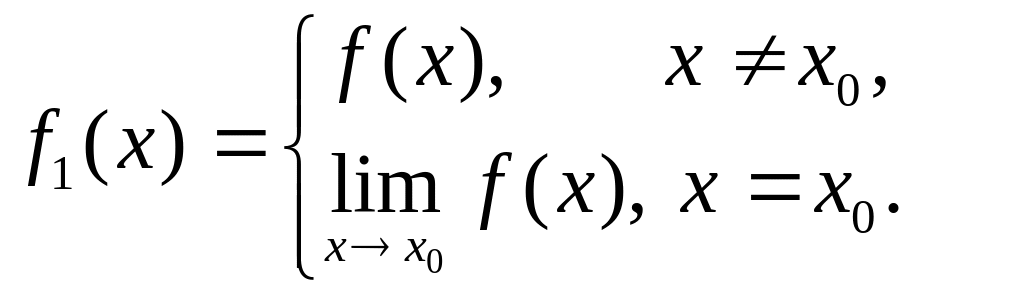
Если: 1) – точка разрыва ,
2) существуют конечные пределы справа и слева:
![]() ,
,
3)
![]()
то точка x0 называется точкой разрыва 1-го рода (неустранимый конечный скачок).

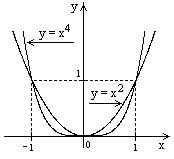
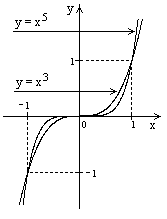

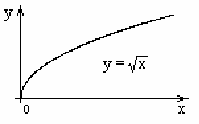
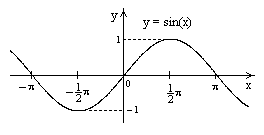
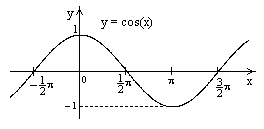
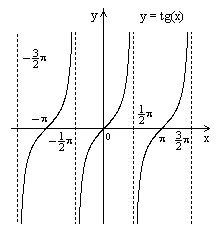
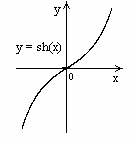
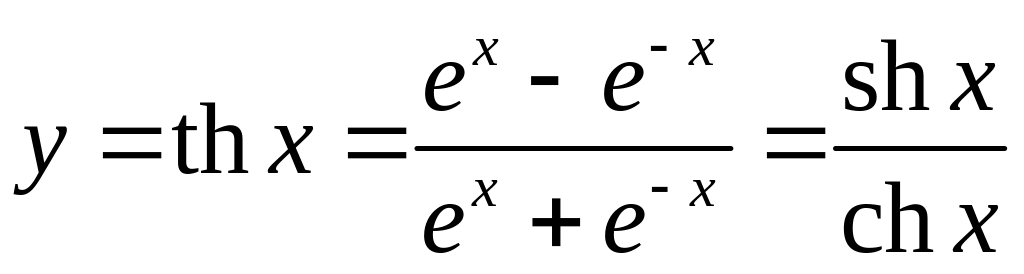 .
.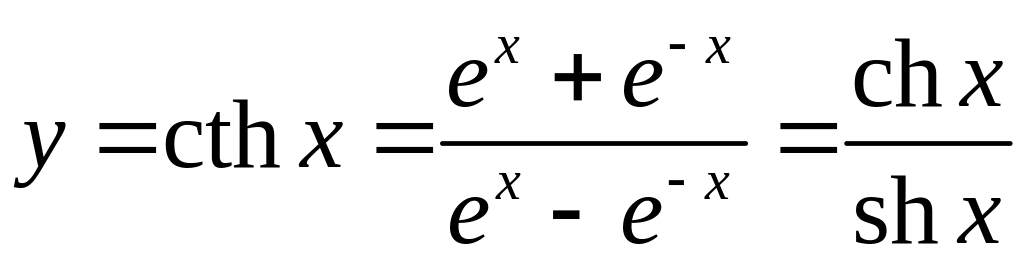 .
.