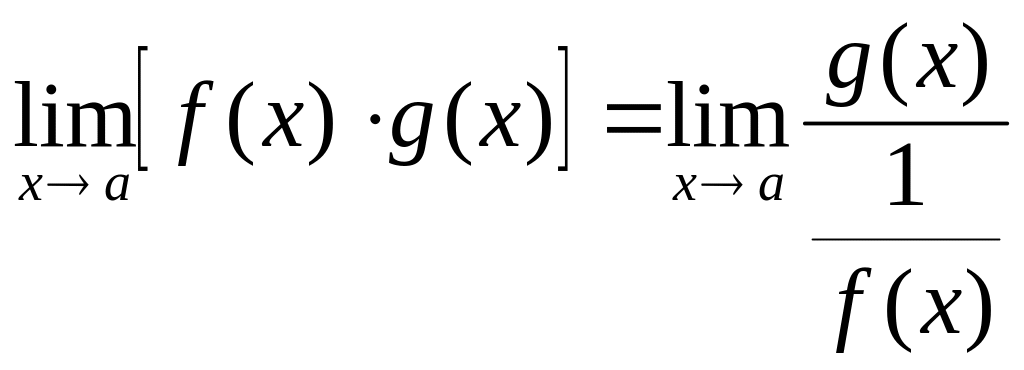Пп 12. Дифференциал. ПРавило лОпиталя.
ФОрмула тейлора
Основные определения и формулы
Дифференциал функции
![]() ,
,
![]()
Главная,
линейная по
![]() часть приращения функции называется
дифференциалом
функции в точке
часть приращения функции называется
дифференциалом
функции в точке
![]() и обозначается
и обозначается
![]() .
.
Главная
часть,
потому что
![]() - бесконечно малая более высокого порядка
малости, чем
.
Линейная,
потому что дифференциал зависит от
в первой степени.
- бесконечно малая более высокого порядка
малости, чем
.
Линейная,
потому что дифференциал зависит от
в первой степени.
![]()
Свойства дифференциалов
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
 .
.
Геометрический смысл дифференциала
Дифференциал
функции
![]() в точке
в точке
![]() равен приращению ординаты касательной
к графику функции в точке
.
равен приращению ординаты касательной
к графику функции в точке
.
Применение дифференциала к приближенным вычислениям
![]() ,
,
![]() ,
,![]()
![]() .
.
Дифференциал сложной функции
![]() ,
,
![]() -
-
инвариантность (неизменность) формы первого дифференциала.
Дифференциалы высших порядков:
,
![]() ,
,![]()
![]() ;
;
![]()
![]()
![]()
В
случае сложной функции, если
![]() ,
,
![]() ,
,
![]() - независимая переменная, тогда
- независимая переменная, тогда
![]()
![]() - форма второго дифференциала не
инвариантна.
- форма второго дифференциала не
инвариантна.
Основные теоремы анализа
Т
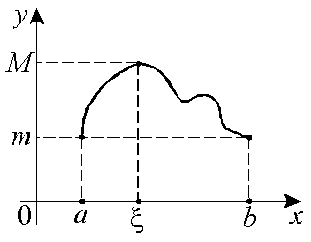 еорема
Ролля
(о
нуле производной)
еорема
Ролля
(о
нуле производной)
Если:
1) функция
![]() - непрерывна на отрезке
- непрерывна на отрезке
![]() ,
2) на интервале
,
2) на интервале
![]() существует производная
существует производная
![]() ,
3) значения функции на концах отрезка
совпадают,
,
3) значения функции на концах отрезка
совпадают,
![]() ,
то существует точка
,
то существует точка
![]() такая, что
такая, что
![]() .
.
Если
функция удовлетворяет условию теоремы
Ролля, то в некоторой точке отрезка
касательная к графику параллельна оси
![]() .
.
Теорема Лагранжа (теорема о конечных приращениях)
Если:
1)
- непрерывна на отрезке
,
2) на интервале
существует производная
,
то существует, по крайней мере, одна
точка
такая, что
![]() или
или
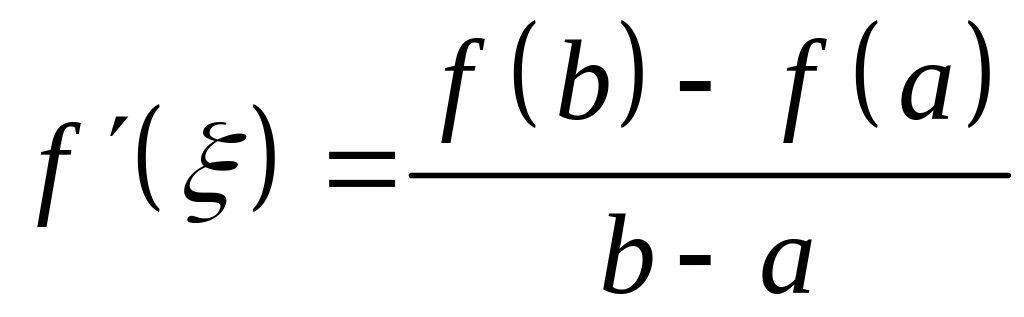 .
.
Н
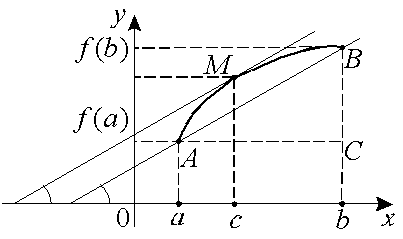 а
кривой
а
кривой
![]() найдется, по крайней мере, одна точка
найдется, по крайней мере, одна точка
![]() ,
в которой касательная параллельна хорде
,
в которой касательная параллельна хорде
![]() .
.
Доказанная
формула называется формулой
Лагранжа
или
формулой
конечных приращений.
Так как
![]() ,
то
,
то
![]() ,
,
![]() ,
где
,
где
![]() ,
откуда
,
откуда
![]() ,
,
![]() .
.
Теорема Коши (обобщенная теорема о конечных разностях)
Если:
1)
![]() непрерывны на
,
2) на
существуют производные
непрерывны на
,
2) на
существуют производные
![]() ,
3)
,
3)
![]()
![]() ,
то существует, по крайней мере, одна
точка
такая, что
,
то существует, по крайней мере, одна
точка
такая, что
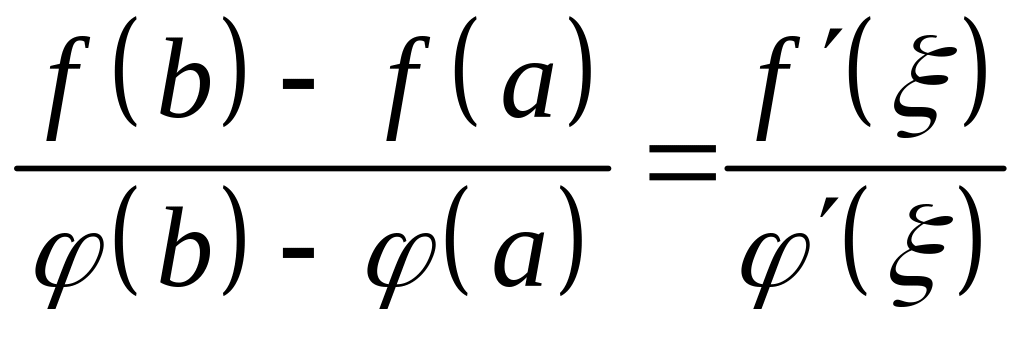 .
.
Правило Лопиталя – Бернулли
Раскрытие
неопределенностей типа
![]() и
и
![]() :
:
 .
.
№п/п |
Неопределенность |
Метод раскрытия |
1 |
|
|
2 |
|
получаем неопределенность или . |
3 |
|
|
4 |
|
Если
Исходный
предел
К
этому же результату можно прийти,
применяя основное логарифмическое
тождество, после чего
|
Многочлен Тейлора
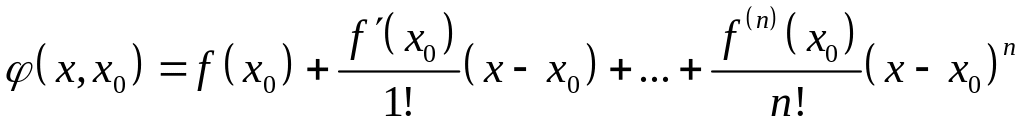 ,
,
Формула Тейлора
Если
дифференцируема
![]() раз в окрестности точки
раз в окрестности точки
![]() ,B
Bто
для любого
,B
Bто
для любого
![]() из указанной окрестности справедлива
формула Тейлора порядка n:
из указанной окрестности справедлива
формула Тейлора порядка n:
![]()
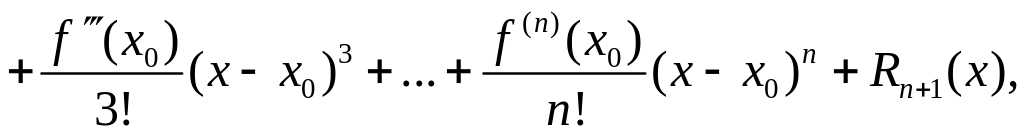
где 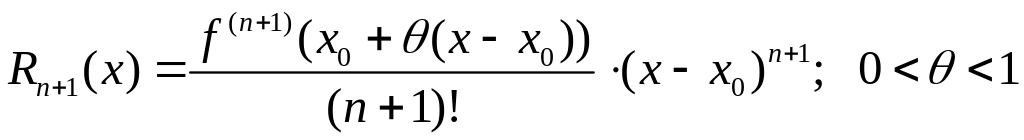 ,
,
![]() называется
остаточным членом в форме Лагранжа.
называется
остаточным членом в форме Лагранжа.
Для вычисления пределов полезен другой вид остаточного члена – в форме Пеано:
=о![]()
Формула Тейлора порядка n позволяет представить функцию в виде суммы многочлена n–й степени и остаточного члена.

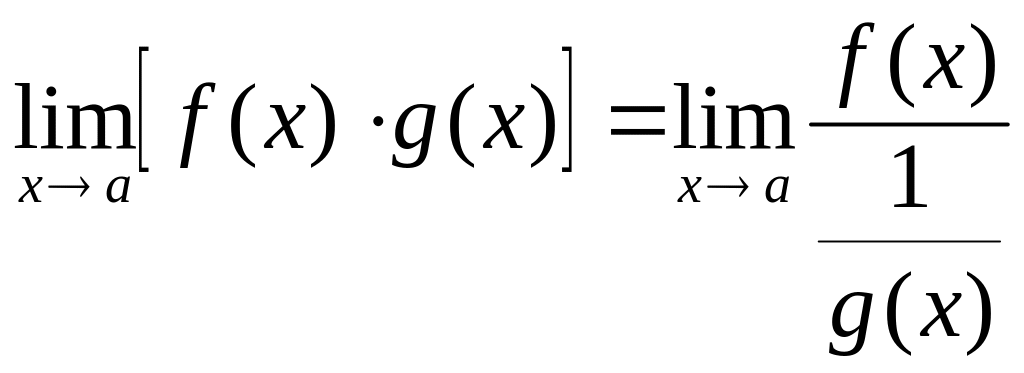 или
или