8.4. Условный экстремум

Пусть открытое множество, и на задана дифференцируемая функция n-переменных 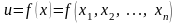. Также на пусть заданы непрерывно-дифференцируемые функции 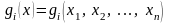, . Будем в дальнейшем предполагать, что 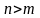и ранг матрицы Якоби

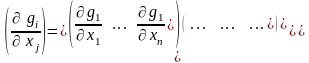равен для .

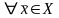Обозначим через 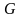множество точек , координаты которых удовлетворяют системе уравнений

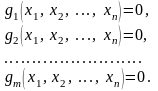(28)

Эти уравнения будем называть уравнениями связи.

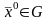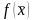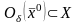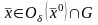Определение 10. Точка называется точкой условного максимума (минимума) функции при выполнении уравнений связи (28), если найдется , что для любой точки выполняется

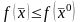
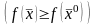. (29)

В отличие от точек обычного локального max или min неравенства (29) выполняются не во всех точках окрестности , а лишь в тех, где выполняются уравнения связи (28). Если точка условного max или min, то она называется точкой условного экстремума.

П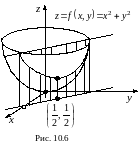 ример 12. Найти условные экстремумы функции 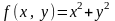при выполнении уравнения связи 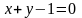(рис. 8.6).

Решение. Из уравнения связи получаем 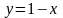. Поэтому при его выполнении функция имеет вид 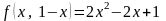. Это функция одной переменной. Найдем ее производную и приравняем ее к нулю

.

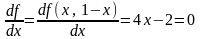Тогда из 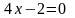получаем, . В силу уравнений связи 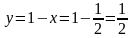, т.е. точка 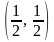стационарная.

Найдем 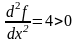. Следовательно, точка является точкой min функции при выполнении условия . Геометрически это означает, что точка параболоида 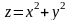проектирующаяся в точке является самой низкой из всех точек, лежащих над прямой 

Этот пример показывает, что точка, в которой функция достигает своего условного экстремума, вообще говоря, не является точкой экстремума самой функции.

Пример 13. Рассмотрим функцию 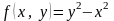(параболический гиперболоид). Уравнение связи 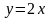– плоскость параллельная оси . Ранее было показано, что функция не имеет экстремума ни в одной точке плоскости . Найдем условный экстремум.

Решение. , .

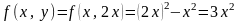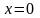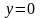Тогда получаем . С учетом связей , и точка 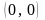является точкой min 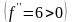. Следовательно, точка есть условный минимум 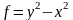при . Таким образом, сама функция не имеет экстремума нигде, но условный экстремум существует. 

Такой метод теоретически можно применить и для более общего случая, когда 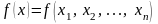, а уравнений связи штук. Пусть, например, 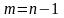. При выполнении условий теоремы 8.5 существует система неявных функций 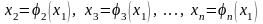(в качестве 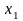можно выбрать и другую переменную), которая после подстановки в 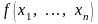дает функцию одной переменной:

,

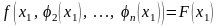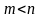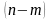которую можно исследовать на экстремум как функцию одной переменной. Аналогично можно рассуждать при любом , тогда по теоремам 8.5 и 8.6 существует система неявных функций, и после их подстановки в 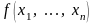получим функцию m-переменных, которую можно теоретически исследовать на экстремум, как функцию многих переменных.

Однако практическое использование такого подхода невозможно, так как решение уравнений связи, т.е. отыскание системы одной или нескольких неявных функций даже в очень простых случаях очень сложно или, чаще всего, невозможно.

Для нахождения условных экстремумов используют метод неопределенных множителей Лагранжа. Запишем матрицу Якоби для системы функций

,

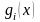
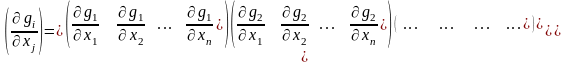т.е. матрицу Якоби можно записать, как векторный столбец градиентов функций .

Теорема 8.11. (Необходимое условие существования условного экстремум). Пусть точка условного экстремума функции при выполнении уравнений связи (29) и градиенты функций 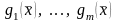линейно независимы ( 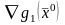, , 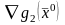…, – линейно независимы), т.е. ранг матрицы Якоби в точке 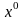равен m. Тогда существуют такие числа 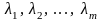, одновременно неравные нулю, что выполняется условие

, (30)

т.е. 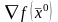является линейной комбинацией градиентов 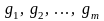. В координатной форме условие (30) имеет вид

. (31)

 Пусть 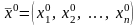точка условного экстремума при условиях (28). По условию ранг матрицы Якоби 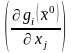равен m, т.е. якобиан

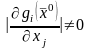. (32)

В силу теоремы 8.5 и замечания о непрерывности достаточно малых и произвольной точки 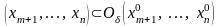система уравнений (31) имеет единственное решение

,

,

,

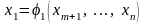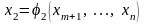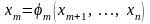удовлетворяющее условиям:

.

При этом функции 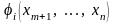непрерывно дифференцируемы и имеют местo тождества (т.к. 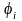– неявные функции задаваемые системой уравнений (31)).

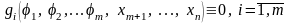, (33)

или .

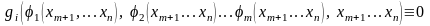Тогда, если подставить в , то получим сложную функцию переменных

.

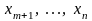
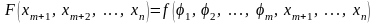Эта функция непрерывная дифференцируемая функция как суперпозиция непрерывных дифференцируемых функций и имеет в точке экстремум, т. к. – точка условного экстремума. Поэтому в этой точке все частные производные по 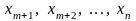равны нулю. Продифференцируем 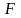как сложную функцию:

или

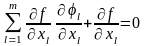. (34)

Теперь продифференцируем по переменным тождество (33)

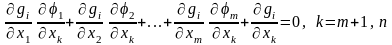
или

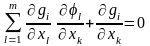. (35)

Система уравнений (34), (35) и есть необходимое условие условного экстремума в точке . Но функции 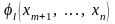в явном виде неизвестны и поэтому, продолжая рассуждения, запишем следующую матрицу Якоби в точке размерности 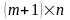, где первой строкой стоит .

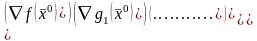(36)

Условия (33) и (34) означают, что каждый из последних 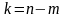столбцов является линейной комбинацией первых столбцов, которые линейно независимы в силу условия (34) теоремы. Следовательно, ранг матрицы (36) тоже равен . Поэтому первая строка матрицы (36) является линейной комбинацией остальных строк, которые линейно независимы.

Следовательно, существуют 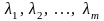одновременно не равные 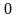, такие, что выполняется (32). 

Точки, в которых выполняются условия (30) и (31), называются стационарными точками при выполнении (30). Эти точки можно определить другим способом, если ввести функцию Лагранжа:

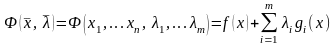. (37)

Числа 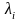называют множителями Лагранжа. Тогда условия (30) или (31) запишутся в виде

.

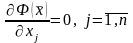Таким образом, стационарные точки функции при выполнении (30) определяются из следующей системы уравнений

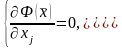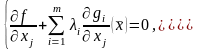или (38)

Поясним геометрический смысл метода Лагранжа. Если 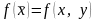, , 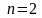, а уравнение связи .

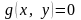Пусть точка условного экстремума при выполнении 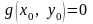. Тогда условия (33) имеют вид

;

;

;

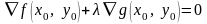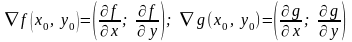Таким образом, градиенты функций и 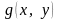коллинеарны в стационарной точке.

Пример 14. Найти экстремум функции 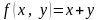при уравнении связи .

Решение. Составим функцию Лагранжа

.

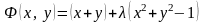Система (38) имеет вид

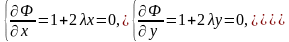
Откуда 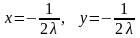. Подставляем в третье уравнение и получаем

, , .

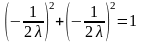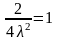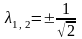Имеем две стационарные точки , .
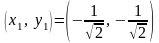
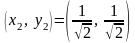