
- •Глава 8. Неявные функции. Дифференцируемые Отображения
- •8.1. Неявные функции заданные одним уравнением
- •8.2. Векторные отображения
- •В силу (13) это будет означать, что
- •Предел отображения обозначается:
- •8.3. Неявные функции n-переменных. Обратные отображения
- •8.4. Условный экстремум
- •8.5. Поверхности в трехмерном евклидовом пространстве
- •8.6. Контрольные вопросы
- •8.7. Примеры решения задач
- •8.8. Задачи для самостоятельного решения
8.6. Контрольные вопросы
1.
Какая функция называется неявной?
Приведите пример уравнения вида
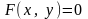 ,
определяющего неявную функцию, и пример
уравнения, не определяющего неявную
функцию.
,
определяющего неявную функцию, и пример
уравнения, не определяющего неявную
функцию.
2.
Сколько непрерывных неявных функций
вида
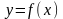 определяет уравнение
определяет уравнение
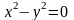 в окрестности точки О(0,
0)?
в окрестности точки О(0,
0)?
3. Сформулируйте теорему о существовании, единственности и непрерывности неявной функции, определяемой уравнением . Докажите существование и единственность этой функции.
4.
Докажите, что уравнение
 не определяет неявную функцию в
прямоугольнике
не определяет неявную функцию в
прямоугольнике
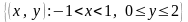 .
Какое условие теоремы 10.1 не выполнено
в данном случае?
.
Какое условие теоремы 10.1 не выполнено
в данном случае?
5.
Приведите примеры, когда невыполнение
условия
 :
:
а) приводит к неразрешимости уравнения относительно у в окрестности точки или к не единственности решения;
б) не нарушает существования и единственности неявной функции вида , определяемой уравнением в окрестности точки .
6.
Докажите, что уравнение
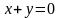 не определяет неявной функции в достаточно
малой окрестности точки (1, 1). Какое
условие теоремы 10.2 не выполнено в данном
случае?
не определяет неявной функции в достаточно
малой окрестности точки (1, 1). Какое
условие теоремы 10.2 не выполнено в данном
случае?
7.
Уравнение
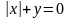 определяет в окрестности точки
определяет в окрестности точки
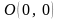 не дифференцируемую в точке
функцию
не дифференцируемую в точке
функцию
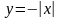 .
Какое условие теоремы 10.2 не выполнено
в данном случае?
.
Какое условие теоремы 10.2 не выполнено
в данном случае?
8.
Уравнение
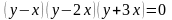 определяет в любой окрестности точки
три
дифференцируемые функции:
определяет в любой окрестности точки
три
дифференцируемые функции:
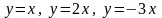 .
Какое условие теоремы 10.2 не выполнено
в данном случае?
.
Какое условие теоремы 10.2 не выполнено
в данном случае?
9.
Вычислите производные
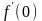 и
и
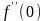 неявной функции
,
определяемой уравнением
и удовлетворяющей условию
неявной функции
,
определяемой уравнением
и удовлетворяющей условию
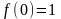 ,
двумя способами: а) используя формулы
(3) и (4); б) используя явное выражение для
функции
,
двумя способами: а) используя формулы
(3) и (4); б) используя явное выражение для
функции
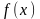 .
.
10. Сформулируйте теорему о существовании, единственности и дифференцируемости совокупности неявных функций, определяемых системой уравнений.
11. Сформулируйте определение условного экстремума функции.
12.
Объясните, в чем состоит метод исключения
части переменных. Сведите задачу об
условном экстремуме функции
 при условии связи
при условии связи
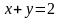 к задаче о безусловном экстремуме.
к задаче о безусловном экстремуме.
13. Что такое функция Лагранжа? Сформулируйте теорему о необходимых условиях Лагранжа условного экстремума.
8.7. Примеры решения задач
1.
Доказать, что уравнение
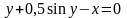 определяют единственную неявную функцию
вида
определяют единственную неявную функцию
вида
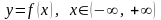 ,
и найти
,
и найти
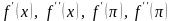 .
.
Решение.
Введем обозначение
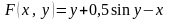 .
Так как
.
Так как
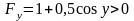 ,
то при любом фиксированном значении х
функция
,
то при любом фиксированном значении х
функция
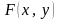 является возрастающей функцией аргумента
у.
Кроме того, для любого фиксированного
значения х
при достаточно больших значениях
является возрастающей функцией аргумента
у.
Кроме того, для любого фиксированного
значения х
при достаточно больших значениях
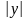 ,
очевидно, выполняются неравенства
,
очевидно, выполняются неравенства
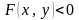 при
при
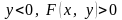 при
при
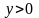 .
Поскольку
– непрерывная функция, отсюда следует,
что
.
Поскольку
– непрерывная функция, отсюда следует,
что
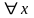 существует единственное у
такое, что
существует единственное у
такое, что
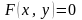 ,
т.е.
уравнение имеет единственное решение
относительно у.
Это и означает, что уравнение определяет
единственную неявную функцию вида
,
т.е.
уравнение имеет единственное решение
относительно у.
Это и означает, что уравнение определяет
единственную неявную функцию вида
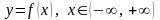 .
.
Так
как
– дифференцируемая функция и
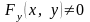 ,
то и функция
дифференцируема на всей числовой прямой.
Для нахождения
,
то и функция
дифференцируема на всей числовой прямой.
Для нахождения
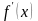 воспользуемся формулой (3):
воспользуемся формулой (3):
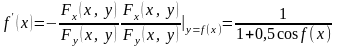
Дифференцируя , найдем
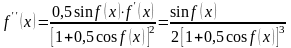 .
.
Чтобы
найти значения
и
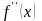 в какой-либо точке х,
нужно сначала вычислить соответствующее
значение
.
Пусть
в какой-либо точке х,
нужно сначала вычислить соответствующее
значение
.
Пусть
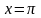 .
Нетрудно проверить, что решением
уравнения при
является
.
Нетрудно проверить, что решением
уравнения при
является
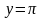 ,
т. е.
,
т. е.
 .
Подставляя
.
Подставляя
 в формулы для
и
,
получаем
в формулы для
и
,
получаем ,
,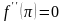 .
.
2.
Найти производные
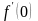 и
и
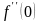 неявной функции
,
заданной
уравнением
неявной функции
,
заданной
уравнением
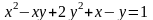 (42)
(42)
и
удовлетворяющей условию
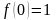 .
.
Решение.
Функция
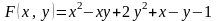 дифференцируема в любой окрестности
точки (0,1). Производная
дифференцируема в любой окрестности
точки (0,1). Производная
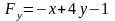 непрерывна в точке (0,1). Наконец,
непрерывна в точке (0,1). Наконец,
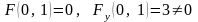 ,
т.е. выполнены все условия теоремы 10.2.
Поэтому в некоторой окрестности точки
(0, 1) уравнение (42) определяет единственную
дифференцируемую неявную функцию вида
,
причем
.
Более того, так
как функция
,
т.е. выполнены все условия теоремы 10.2.
Поэтому в некоторой окрестности точки
(0, 1) уравнение (42) определяет единственную
дифференцируемую неявную функцию вида
,
причем
.
Более того, так
как функция
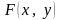 дважды
дифференцируема в любой окрестности
точки (0, 1), то и функция
дважды дифференцируема в некоторой
окрестности точки
.
дважды
дифференцируема в любой окрестности
точки (0, 1), то и функция
дважды дифференцируема в некоторой
окрестности точки
.
Производные
и
можно найти по правилу дифференцирования
неявных функций, а затем, полагая
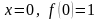 ,
вычислить
и
.
Однако удобнее
поступить следующим образом. Предполагая,
что функция
подставлена в уравнение (42), продифференцируем
полученное тождество
по х:
,
вычислить
и
.
Однако удобнее
поступить следующим образом. Предполагая,
что функция
подставлена в уравнение (42), продифференцируем
полученное тождество
по х:
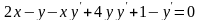 .
(43)
.
(43)
Полагая
в равенстве (43)
,
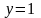 ,
получаем
,
получаем
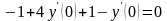 ,
откуда
,
откуда
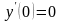 .
Чтобы найти вторую производную,
продифференцируем тождество (42) по х:
.
Чтобы найти вторую производную,
продифференцируем тождество (42) по х:
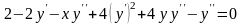 .
.
Полагая
,
,
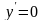 ,
получаем
,
получаем
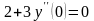 ,
откуда
,
откуда
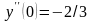 .
Итак,
.
Итак,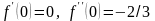 .
.
3. Найти производные первого и второго порядков неявной функции , заданной уравнением
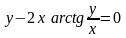 .
(44)
.
(44)
Решение.
Левая часть уравнения (44) не определена
при
.
Будем считать, что
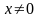 .
Предположим, что уравнение (44) определяет
дважды дифференцируемую неявную функцию
.
Подставляя ее и дифференцируя полученное
тождество по х,
приходим
к равенству
.
Предположим, что уравнение (44) определяет
дважды дифференцируемую неявную функцию
.
Подставляя ее и дифференцируя полученное
тождество по х,
приходим
к равенству
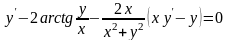 .
(45)
.
(45)
Уравнение
(45) можно упростить, если воспользоваться
исходным уравнением (44). А именно, из
уравнения (44) следует,
 .
Поэтому
уравнение (45) можно записать так:
.
Поэтому
уравнение (45) можно записать так:
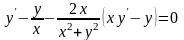
Отсюда находим
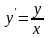 .
(46)
.
(46)
где . Для вычисления второй производной можно продифференцировать тождество (45) по х и, получив линейное относительно у" уравнение, найти вторую производную. Однако в данном случае удобнее воспользоваться равенством (46), из которого следует
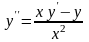 .
.
Подставляя
в последнее равенство выражение для
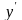 ,
окончательно находим
,
окончательно находим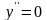 .
.
4. Методом исключения переменных найти экстремум функции
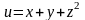 (47)
(47)
при условиях связи
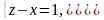 (48)
(48)
Решение. Решая систему уравнений (54) относительно y и z, находим
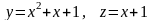 .
(49)
.
(49)
Подставляя
выражение (49) в равенство (47), приходим
к функции одной переменной
:
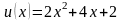 ,
для которой рассмотрим задачу о
безусловном экстремуме. Так как
,
для которой рассмотрим задачу о
безусловном экстремуме. Так как
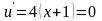 при
при
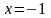 ,
то функция
,
то функция
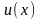 имеет единственную точку возможного
экстремума. Но
имеет единственную точку возможного
экстремума. Но
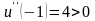 ,
поэтому при
функция
имеет минимум. Из системы (55) находим
соответствующие
значения у
и
:
,
поэтому при
функция
имеет минимум. Из системы (55) находим
соответствующие
значения у
и
:
 .
Итак, функция (47) при условиях связи (48)
имеет в точке
.
Итак, функция (47) при условиях связи (48)
имеет в точке
 минимум, причем
минимум, причем
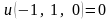 .
.
5. Методом Лагранжа найти экстремум функции (47) при условиях связи (48).
Решение. Составим функцию Лагранжа
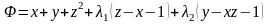
и рассмотрим систему уравнений:

Она
имеет единственное решение:
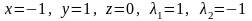 ,
т. е.
,
т. е.
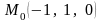 – единственная точка возможного
экстремума функции (47) при условиях
связи (48). Отметим, что в окрестности
точки
система (48) определяет единственную
пару неявных функций
– единственная точка возможного
экстремума функции (47) при условиях
связи (48). Отметим, что в окрестности
точки
система (48) определяет единственную
пару неявных функций
 ,
,
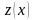 .
Хотя
в данном случае их легко найти в явном
виде,
нам эти явные выражения не понадобятся.
Предполагая, что в систему (48) подставлено
ее решение
,
,
и
дифференцируя полученные
тождества, приходим к равенствам
.
Хотя
в данном случае их легко найти в явном
виде,
нам эти явные выражения не понадобятся.
Предполагая, что в систему (48) подставлено
ее решение
,
,
и
дифференцируя полученные
тождества, приходим к равенствам
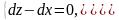
Отсюда находим
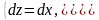 (
(
Теперь вычисляем второй дифференциал функции Лагранжа:
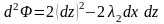 ,
,
и,
подставляя
 и выражение (54) для dz,
получаем положительно определенную
квадратичную форму от одной переменной
и выражение (54) для dz,
получаем положительно определенную
квадратичную форму от одной переменной
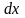 :
:
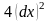 .
Отсюда следует, что функция (47) при
условиях связи (48) имеет в точке
условный минимум.
.
Отсюда следует, что функция (47) при
условиях связи (48) имеет в точке
условный минимум.
