§7. Закон больших чисел и предельные теоремы

При изучении массовых однородных случайных явлений обнаруживаются определенные устойчивые закономерности, которые проявляются тем точнее, чем большее число явлений рассматривается. Приведем несколько примеров.

Пример 1. Организуется или реорганизуется работа столовой с целью повышения качества обслуживания. Неизвестно какое количество посетителей придет в нее в определенные промежутки времени, какие блюда они будут заказывать, и сколько времени будет продолжаться обслуживание каждого посетителя. Однако существуют вполне определенные средние величины, которые позволяют укомплектовать столовую обслуживающим персоналом, оборудованием, завезти необходимое количество продуктов и т.д.

Пример 2. Организуется система профилактического и аварийного ремонта техники на предприятии с целью уменьшения простоев за счет неисправностей и ремонтов. Отказы техники, длительность простоев из-за ремонтов и профилактик носят случайный характер. Однако существуют устойчивые величины, которые позволяют эффективно проводить ремонтные и профилактические работы на предприятии.

Таких примеров можно привести множество. Во всех этих примерах проявляется общий принцип закона больших чисел, который академик А.Н. Колмогоров сформулировал следующим образом: «Совокупное действие большого числа случайных факторов приводит (при некоторых, весьма общих, условиях) к результату почти не зависящему от случая». Иначе закон больших чисел можно сформулировать следующим образом: при большом числе случайных величин их средний результат перестает быть случайным и его можно предсказать с большой степенью определенности. На этом положении основано практическое применение закона больших чисел..

Нас закон больших чисел будет интересовать с математической точки зрении, а именно, при каких условиях случайные величины подчиняются закону больших чисел. Эти вопросы решаются с помощью теорем Маркова, Чебышева, Бернулли, которые составляют сущность закона больших чисел в узком смысле.

7.1. Неравенство Маркова.

Теорема. Если случайная величина принимает только неотрицательные значения и существует ее математическое ожидание , то для любого положительного числа выполняется неравенство

. (1)

Неравенство (1) будем называть первым неравенством Маркова.

Доказательство проведем для дискретной случайной величины , закон распределения которой задан таблицей 7.1.

Таблица 7.1.

			…			…
			…			…

Будем предполагать, что случайная величина принимает только неотрицательные значения, причем все возможные значения случайной величины расположены в таблице в порядке возрастания.

Найдем математическое ожидание случайной величины

. (2)

Пусть заданное число. Тогда относительно значений случайной величины может занимать следующие три положения.

Первый случай. Число расположено между значениями случайной величины , т.е. первые значений случайной величины не больше

… …	, (3) а все остальные значения больше . (4)

Отбросив в формуле (2) первых неотрицательных слагаемых, получим неравенство вида

.

Заменим в последнем неравенстве все числом . С учетом неравенств (4) получим более сильное неравенство

.

Так как

,

то из неравенства

следует неравенство Маркова вида

.

Второй случай. Все значения случайной величины не больше числа , т.е.

… …	, В этом случае случайная величина не может принять значение большее числа .

Поэтому

.

В этом случае неравенство (1) очевидно.

Третий случай. Все значения случайной величины больше числа , т.е.

… …	. В этом случае, с одной стороны, ,

а, с другой стороны,

.

Следовательно, в этом случае неравенство Маркова (1) также справедливо.

Следствие. Если случайная величина принимает только неотрицательные значения и существует ее математическое ожидание , то для любого положительного числа выполняется неравенство

. (5)

Неравенство (5) будем называть вторым неравенством Маркова.

Доказательство. Так как события и являются противоположными, то

,

откуда с учетом неравенства Маркова (1) получаем второе неравенство Маркова

.

Пример. Отделение банка обслуживает в среднем 100 клиентов в день. Оцените вероятность того, что в определенный день в отделении банка будет обслужено:

а) не более 200 клиентов;

б) более 150 клиентов.

Решение. Ведем обозначения. Пусть

число клиентов, обслуживаемых в отделении банка в течение дня,

,

.

Тогда требуется оценить вероятность а) ;

б) .

а) Для того чтобы оценить вероятность воспользуемся вторым неравенством Маркова (5). Подставляя в неравенство данные задачи, получим

.

б) Оценим вероятность того, что в определенный день в отделении банка будет обслужено более 150 клиентов. Для этого, подставляя в первое неравенство Маркова, данные задачи, находим

.

Пример. Сумма всех вкладов в отделение банка со­ставляет 2 млн гр., а вероятность того, что случайно взятый вклад не превысит 10 тыс. гр., равна 0,6. Что можно сказать о числе вкладчиков.

Решение. Ведем обозначения. Пусть

размер случайно взятого вклада;

число всех вкладчиков банка.

Требуется оценить число вкладчиков банка.

Так как сумма всех вкладов в отделение банка со­ставляет 2 млн гр., а п — число всех вкладчиков, то средний размер вклада

(тыс. гр.).

Согласно второму неравенству Маркова получаем

.

Так как по условию задачи , то

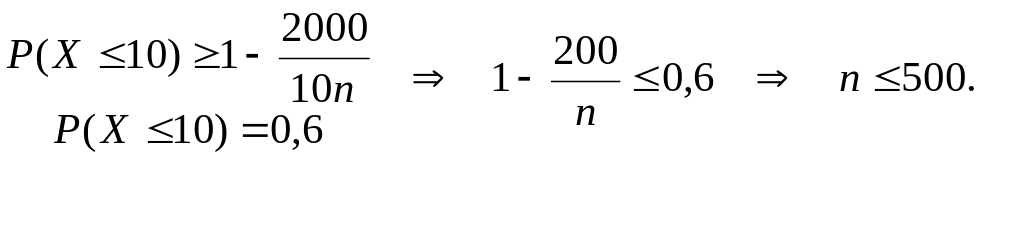
Таким образом, число вкладчиков банка не более 500.